La derivada de la cosecante al cuadrado es igual a menos dos tiempos contingentes de la cosecante al cuadrado, -2cot(x)csc2(x). Podemos encontrar esta derivada usando la regla de la cadena y las derivadas de las funciones trigonométricas fundamentales.
Aquí, veremos una demostración de esta derivada, la comparación gráfica de la cosecante al cuadrado y su derivada, y algunos ejemplos.
CÁLCULO
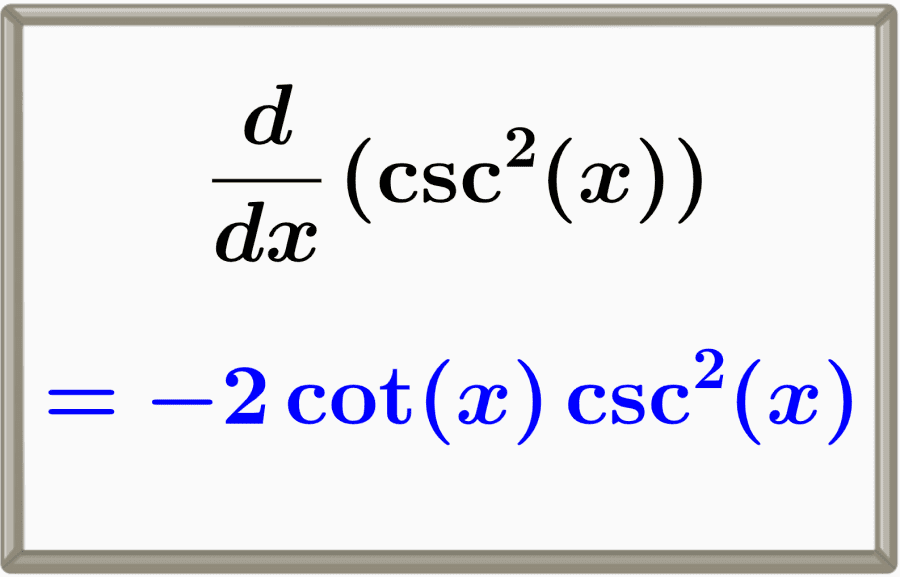
Relevante para…
Aprender a encontrar la derivada de la cosecante al cuadrado.
- Demostración de la derivada de la cosecante al cuadrado con la regla de la cadena
- Relación entre la derivada de la cosecante al cuadrado y la cotangente al cuadrado
- Gráfica de cosecante al cuadrado de x vs. la derivada de la cosecante al cuadrado x
- Ejemplos
- Práctica de derivadas de funciones cosecante cuadrado
- Véase también
CÁLCULO
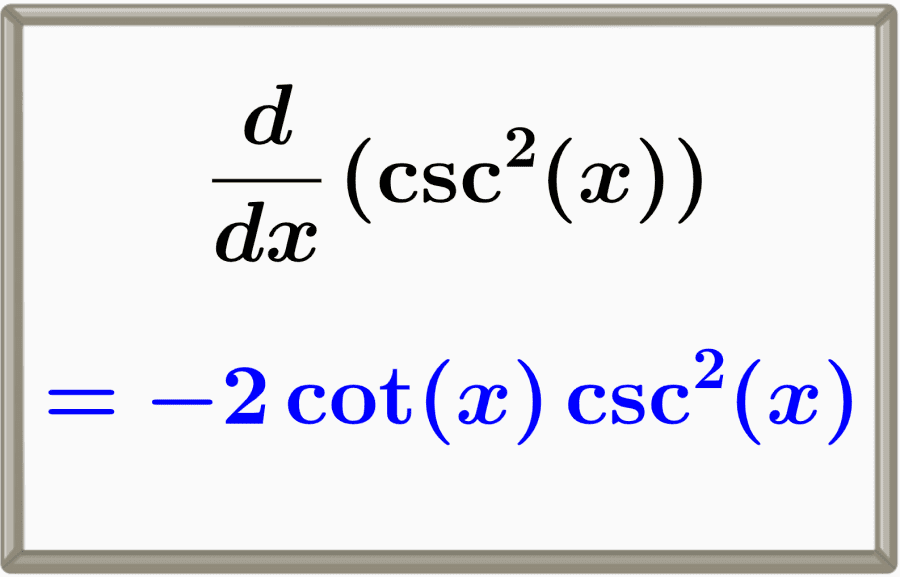
Relevante para…
Aprender a encontrar la derivada de la cosecante al cuadrado.
Demostración de la derivada de la cosecante al cuadrado con la regla de la cadena
Como requisito previo, revise la fórmula de la regla de la cadena y su demostración consultando el artículo: Regla de la Cadena. Del mismo modo, puedes revisar la demostración de la función derivada de la cosecante visitando este artículo: Derivada de Cosecante, csc(x).
Recordemos que
$latex \csc^{2}{(x)} \neq \csc{(x^2)}$
Esta es una función cosecante compuesta, por lo que puede ser derivada usando la regla de la cadena. Entonces, empezamos con la función:
$latex F(x) = \csc^{2}{(x)}$
Podemos identificar las dos funciones que componen F(x). Una función está elevada a una potencia de dos y la otra es una función trigonométrica de cosecante.
Si es que reescribimos a la función de la siguiente forma, podemos ver esto más claramente:
$latex F(x) = \csc^{2}{(x)}$
$latex F(x) = (\csc{(x)})^2$
Ahora es claro que la función de potencia es la función externa, mientras que la función cosecante, es la función interna. Podemos configurar la función externa de la siguiente manera:
$latex f(u) = u^2$
en donde
$latex u = \csc{(x)}$
La función cosecante trigonométrica, como función interna de f(u), se denotará como g(x).
$latex f(u) = f(g(x))$
$latex u = g(x)$
$latex g(x) = \csc{(x)}$
Derivando la función externa f(u) usando la regla de la potencia en términos de u, tenemos
$latex f(u) = u^2$
$latex f'(u) = 2u$
Derivando la función interna g(x) usando la fórmula derivada de la función trigonométrica cosecante en términos de x, tenemos
$latex g(x) = \csc{(x)}$
$latex g'(x) = -\csc{(x)}\cot{(x)}$
Multiplicando algebraicamente la derivada de la función exterior $latex f'(u)$ por la derivada de la función interior $latex g'(x)$, tenemos
$latex \frac{dy}{dx} = f'(u) \cdot g'(x)$
$latex \frac{dy}{dx} = (2u) \cdot (-\csc{(x)}\cot{(x)})$
Sustituyendo u en f‘(u), tenemos
$latex \frac{dy}{dx} = (2(\csc{(x)})) \cdot (-\csc{(x)}\cot{(x)})$
$latex \frac{dy}{dx} = -(2(\csc{(x)})) \cdot (\csc{(x)}\cot{(x)})$
$latex \frac{dy}{dx} = -2\csc^{2}{(x)} \cdot \cot{(x)}$
lo que nos lleva a la fórmula de la derivada de la cosecante al cuadrado x
$latex \frac{d}{dx} \csc^{2}{(x)} = -2\cot{(x)}\csc^{2}{(x)}$
Relación entre la derivada de la cosecante al cuadrado y la cotangente al cuadrado
Tal vez te preguntes porqué
$latex \csc^{2}{(x)}$
y
$latex \cot^{2}{(x)}$
tienen derivadas similares.
De acuerdo con la fórmula de Pitágoras para cosecantes y cotangentes,
$latex \csc^{2}{(x)} = 1 + \cot^{2}{(x)}$
Si tratamos de derivar ambos lados de la ecuación, tenemos
$latex \frac{d}{dx} (\csc^{2}{(x)}) = \frac{d}{dx}(1) + \frac{d}{dx}(\cot^{2}{(x)})$
La derivada de una constante es igual a cero, entonces:
$latex \frac{d}{dx} (\csc^{2}{(x)}) = 0 + \frac{d}{dx}(\cot^{2}{(x)})$
$latex \frac{d}{dx} (\csc^{2}{(x)}) = \frac{d}{dx}(\cot^{2}{(x)})$
Por eso tanto la cosecante al cuadrado como la cotangente al cuadrado tienen la misma derivada, por la fórmula pitagórica de las cosecantes y cotangentes.
Gráfica de cosecante al cuadrado de x vs. la derivada de la cosecante al cuadrado x
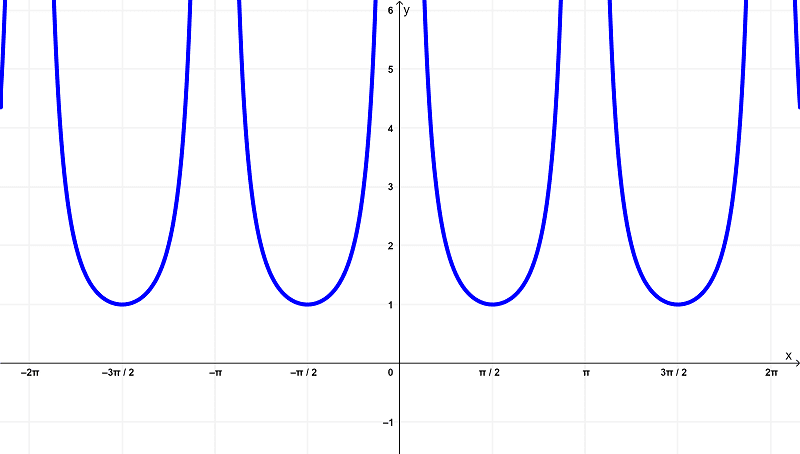
Dada la función
$latex f(x) = \csc^{2}{(x)}$
su gráfica es
Como ya sabemos, la derivada de $latex f(x) = \csc^{2}{(x)}$ es
$latex f'(x) = -2\cot{(x)}\csc^{2}{(x)}$
que se grafica como
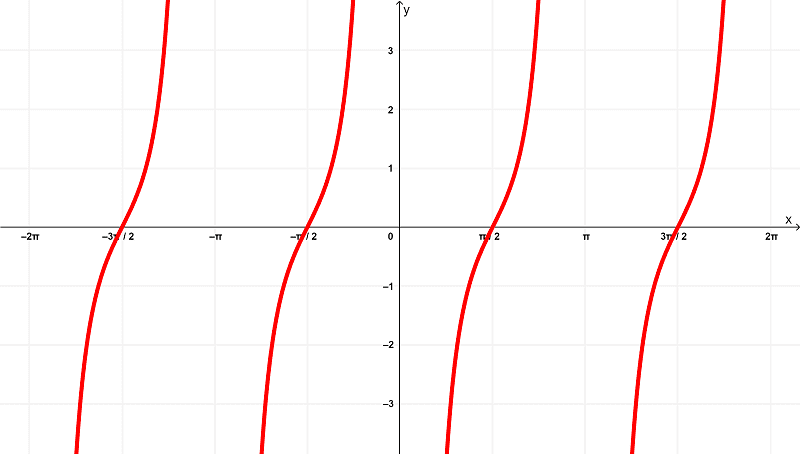
Ilustrando ambas gráficas en una, tenemos
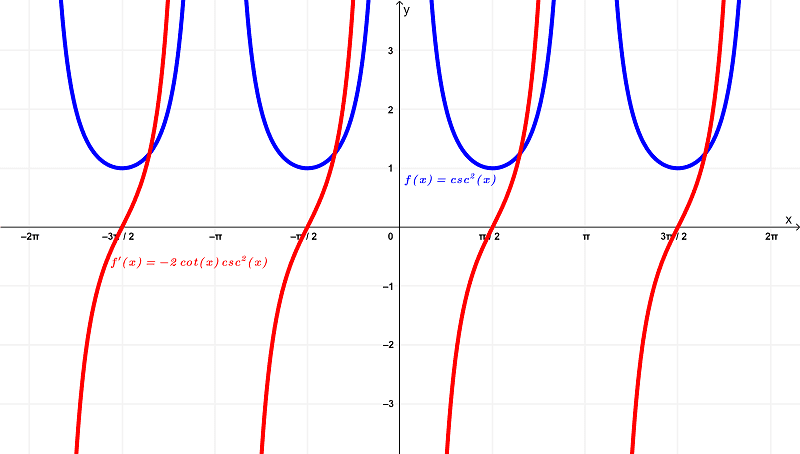
Al examinar las diferencias entre estas funciones basándote en los gráficos anteriores, puedes ver que la función original $latex f(x) = \csc^{2}{(x)}$ tiene un dominio de
$$(-2\pi,-\pi) \cup (-\pi,0) \cup (0,\pi) \cup (\pi,2\pi)$$
dentro de los intervalos finitos de
$latex (-2\pi,2\pi)$
y se encuentra dentro del rango de
$latex [1,\infty)$
mientras que la derivada $latex f'(x) = -2\cot{(x)}\csc^{2}{(x)}$ tiene un dominio de
$$(-2\pi,-\pi) \cup (-\pi,0) \cup (0,\pi) \cup (\pi,2\pi)$$
dentro de los intervalos finitos de
$latex (-2\pi,2\pi)$
y se encuentra dentro del rango de
$latex (-\infty,\infty)$
Ejemplos
En los siguientes ejemplos, podemos observar cómo derivar una función cosecante al cuadrado compuesta.
EJEMPLO 1
Determina la derivada de la función $latex f(x) = \csc^2(15x)$.
Solución
Esta es una función cosecante al cuadrado compuesta, por lo que el uso de la regla de la cadena es requerido para encontrar su derivada.
Entonces, vamos a tomar a $latex u=15x$ como la función interna, por lo que tenemos $latex f(u)=\csc^2(u)$. Con la regla de la cadena, esto nos da:
$$\frac{dy}{dx}=\frac{dy}{du} \frac{du}{dx}$$
$$\frac{dy}{dx}=-2\cot(u)\csc^2(u) \times 15$$
Solo nos queda sustituir $latex u=15x$ de vuelta en la función y tenemos:
$$\frac{dy}{dx}=-30\cot(15x)\csc^2(15x)$$
EJEMPLO 2
Encuentra la derivada de la función $latex F(x) = \csc^2(6x^3-8x)$
Solución
En este caso, la función interna es $latex 6x^3-8x$, lo que nos permite escribir $latex f (u) = \csc^2(u)$.
Entonces, podemos encontrar la derivada de la función externa
$$\frac{d}{du} ( \csc^2(u) ) = -2\cot(u)\csc^2(u)$$
Calculando la derivada de $latex g(x)=u=6x^3-8x$, tenemos:
$$\frac{d}{dx}(g(x)) = \frac{d}{dx}(6x^3-8x)$$
$$\frac{d}{dx}(g(x)) = 18x^2-8$$
Multiplicando a la derivada de la función externa $latex f(u)$ por la derivada de la función interna $latex g(x)$, tenemos:
$$\frac{dy}{dx} = \frac{d}{du} (f(u)) \cdot \frac{d}{dx} (g(x))$$
$$\frac{dy}{dx} = -2\cot(u)\csc^2(u) \cdot (18x^2-8)$$
Finalmente, aplicamos la sustitución $latex u=6x^3-8x$ y simplificamos:
$$\frac{dy}{dx} = -2\cot(6x^3-8x)\csc^2(6x^3-8x) \cdot (18x^2-8)$$
$$\frac{dy}{dx} = -(36x^2-16)\cot(6x^3-8x)\csc^2(6x^3-8x)$$
Práctica de derivadas de funciones cosecante cuadrado


Véase también
¿Interesado en aprender más sobre derivadas de funciones trigonométricas al cuadrado? Mira estas páginas:
- Derivada de seno al cuadrado, sin^2(x) – Demostración y Gráficas
- Derivada de coseno al cuadrado, cos^2(x) – Demostración y Gráficas
- Derivada de tangente al cuadrado, tan^2(x) – Demostración y Gráficas
- Derivada de secante al cuadrado, sec^2(x) – Demostración y Gráficas
- Derivada de cotangente al cuadrado, cot^2(x) – Demostración y Gráficas


