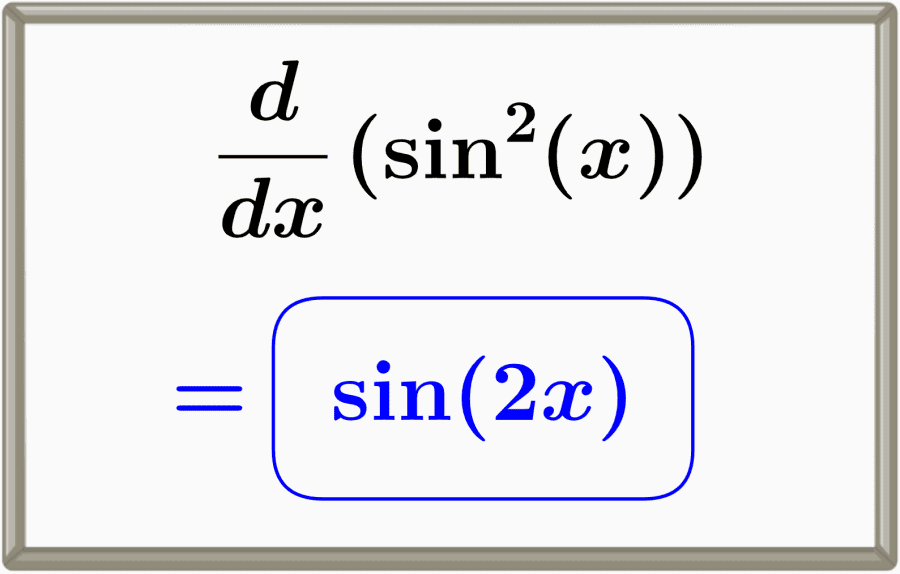La derivada de la función seno al cuadrado es igual al seno de 2x, sin(2x). Podemos encontrar esta derivada usando la regla de la cadena y las derivadas de las funciones trigonométricas fundamentales.
En este artículo, veremos cómo calcular la derivada de la función compuesta seno al cuadrado. Veremos una demostración, la comparación gráfica de seno cuadrado de x su y derivada, y algunos ejemplos.
Demostración de la función derivada de seno cuadrado usando la regla de la cadena
Si lo necesitas, recomendamos revisar la fórmula de la regla de la cadena, como requisito previo de este tema, visitando este enlace: Regla de la Cadena. Asimismo, puede visitar este otro enlace para la demostración de la función derivada del seno: Derivada de Seno, sin(x).
Ten en cuenta que
$latex \sin^{2}{(x)} \neq \sin{(x^2)}$
Dejando a un lado la confusión, la primera es una «función trigonométrica completa» elevada a la potencia de dos, mientras que la segunda es una función trigonométrica de «una variable elevada a la potencia de dos».
Debido a que es una función compuesta, la fórmula de la regla de la cadena se usa para encontrar la fórmula derivada de la función seno al cuadrado, siempre que ya haya dominado la fórmula de la regla de la cadena y la función derivada del seno.
Supongamos que nos piden obtener la derivada de
$latex F(x) = \sin^{2}{(x)}$
Podemos identificar las dos funciones que componen F(x). Hay una función de potencia y una función trigonométrica en este escenario. Basándonos en nuestra F(x) dada, son una función elevada a una potencia de dos y una función trigonométrica de seno.
Para una representación más fácil, podemos reescribir esto como
$latex F(x) = \sin^{2}{(x)}$
$latex F(x) = (\sin{(x)})^2$
Es evidente ahora que la función potencia dada es la función exterior, mientras que la función seno al cuadrado por la función potencia dada es la función interior. Podemos establecer la función externa como
$latex f(u) = u^2$
en donde
$latex u = \sin{(x)}$
Estableciendo la función seno trigonométrica como la función interna de f(u) denotándola como g(x), tenemos
$latex f(u) = f(g(x))$
$latex g(x) = \sin{(x)}$
$latex u = g(x)$
Derivando la función externa f(u) usando la regla de la potencia en términos de u, tenemos
$latex f(u) = u^2$
$latex f^{\prime}(u) = 2u$
Derivando la función interna g(x) usando la fórmula derivada de la función trigonométrica seno en términos de x, tenemos
$latex g(x) = \sin{(x)}$
$latex g^{\prime}(x) = \cos{(x)}$
Multiplicando algebraicamente la derivada de la función exterior $latex f^{\prime}(u)$ por la derivada de la función interior $latex g^{\prime}(x)$, tenemos
$latex \frac{dy}{dx} = f^{\prime}(u) \cdot g^{\prime}(x)$
$latex \frac{dy}{dx} = (2u) \cdot (\cos{(x)})$
Sustituyendo u en f‘(u), tenemos
$latex \frac{dy}{dx} = (2(\sin{(x)})) \cdot (\cos{(x)})$
$latex \frac{dy}{dx} = 2\sin{(x)}\cos{(x)}$
Aplicando las identidades de doble ángulo, tenemos
$latex \frac{dy}{dx} = \sin{(2x)}$
Esto nos lleva a la fórmula derivada del seno al cuadrado x.
$latex \frac{d}{dx} \sin^{2}{(x)} = \sin{(2x)}$
Gráfica de seno cuadrado de x vs. la derivada del seno al cuadrado de x
Dada la función
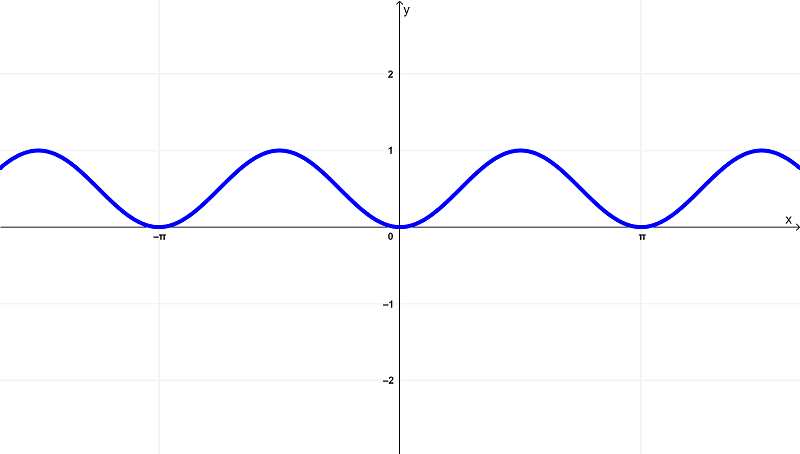
$latex f(x) = \sin^{2}{(x)}$
su gráfica es
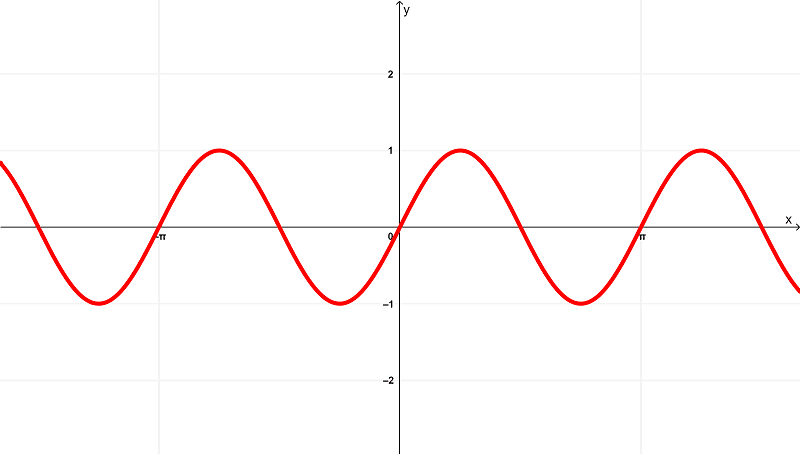
Al derivar a la función $latex f(x) = \sin^{2}{(x)}$, obtenemos
$latex f'(x) = \sin{(2x)}$
que si se representa gráficamente, muestra
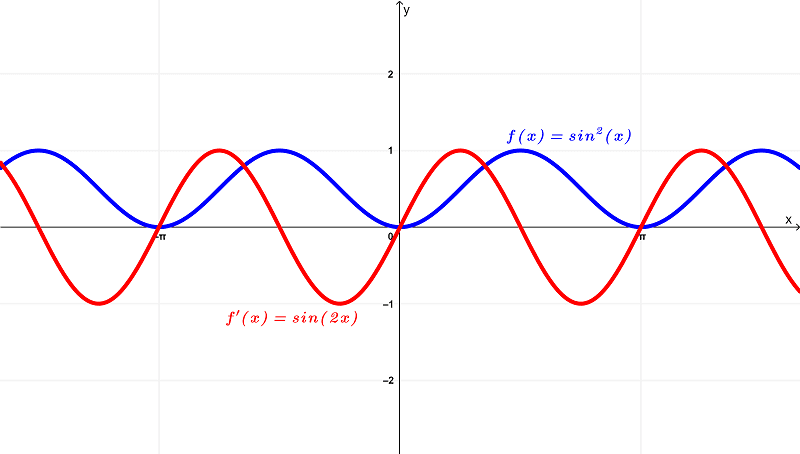
Ilustrando ambas gráficas en una, tenemos
Mirando las diferencias entre estas funciones basadas en esos gráficos, puedes ver que la función original $latex f(x) = sin^{2}{(x)}$ tiene un dominio de
$latex (-\infty,\infty)$ o todos los números reales
y existe dentro del rango de
$latex [0,1]$
mientras que la derivada $latex f'(x) = \sin{(2x)}$ tiene un dominio de
$latex (-\infty,\infty)$ o todos los números reales
y existe dentro del rango de
$latex [-1,1]$
Ejemplos
En los siguientes ejemplos, podemos aprender cómo derivar funciones seno cuadrado compuestas.
EJEMPLO 1
Encuentra la derivada de $latex f(x) = \sin^2(6x)$
Solución
Podemos usar la regla de la cadena porque tenemos una función seno cuadrado compuesta en donde $latex 6x$ es la función interna.
Si es que escribimos $latex u=6x$, tenemos $latex f(u)=\sin^2(u)$. Entonces, al usar la regla de la cadena, tenemos:
$$\frac{dy}{dx}=\frac{dy}{du} \frac{du}{dx}$$
$$\frac{dy}{dx}=\sin(2u) \times 6$$
Sustituyendo $latex u=6x$ de vuelta en la función, tenemos:
$$\frac{dy}{dx}=6\sin(12x)$$
EJEMPLO 2
¿Cuál es la derivada de $latex F(x) = \sin^2(3x^2-5)$?
Solución
Vamos a usar la regla de la cadena con la sustitución $latex u=2x^2+3$. Entonces, podemos escribir a la función original como $latex f (u) = \sin^2(u)$.
Ahora, vamos a encontrar la derivada de la función externa:
$$\frac{d}{du} ( \sin^2(u) ) = \sin(2u)$$
Luego, encontramos la derivada de la función interna $latex g(x)$ o $latex u$:
$$\frac{d}{dx}(g(x)) = \frac{d}{dx}(3x^2-5)$$
$$\frac{d}{dx}(g(x)) = 6x$$
Para aplicar la regla de la cadena, tenemos que multiplicar la derivada de la función externa $latex f(u)$ por la derivada de la función interna $latex g(x)$:
$$\frac{dy}{dx} = \frac{d}{du} (f(u)) \cdot \frac{d}{dx} (g(x))$$
$$\frac{dy}{dx} = \sin(2u) \cdot 6x$$
Finalmente, substituimos $latex u=3x^2-5$ y simplificamos:
$$\frac{dy}{dx} = \sin(2(3x^2-5)) \cdot 6x$$
$$\frac{dy}{dx} = 6x\sin(6x^2-10)$$
Práctica de derivadas de funciones seno cuadrado
Véase también
¿Interesado en aprender más sobre derivadas de funciones trigonométricas al cuadrado? Mira estas páginas:
- Derivada de coseno al cuadrado, cos^2(x) – Demostración y Gráficas
- Derivada de tangente al cuadrado, tan^2(x) – Demostración y Gráficas
- Derivada de secante al cuadrado, sec^2(x) – Demostración y Gráficas
- Derivada de cosecante al cuadrado, csc^2(x) – Demostración y Gráficas
- Derivada de cotangente al cuadrado, cot^2(x) – Demostración y Gráficas
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
