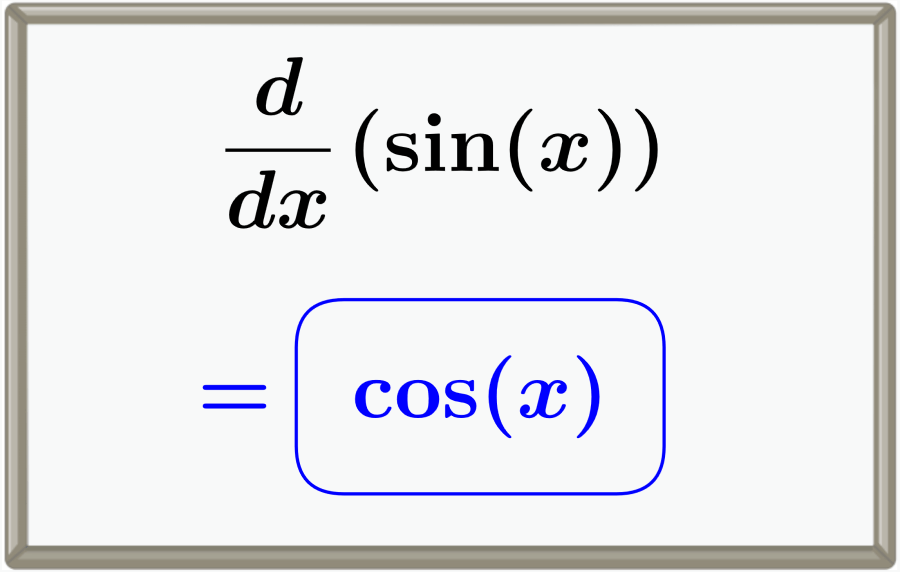La Derivada del Seno es una de las primeras funciones trascendentales introducidas en Cálculo Diferencial (o Cálculo I). La derivada del seno es igual al coseno, cos(x). Esta derivada se puede demostrar usando límites y las identidades trigonométricas.
En este artículo, conoceremos cómo derivar la función trigonométrica seno. Aprenderemos sobre su fórmula, veremos una comparación gráfica del seno y su derivada, y terminaremos con algunos ejemplos.
CÁLCULO
Relevante para…
Aprender sobre la demostración y gráficas de la derivada del seno.
CÁLCULO
Relevante para…
Aprender sobre la demostración y gráficas de la derivada del seno.
Demostración de la derivada de la función seno
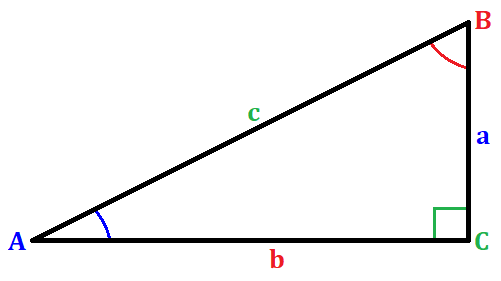
La función trigonométrica seno de un ángulo se define como la relación de un lado opuesto a un ángulo en un triángulo rectángulo a la hipotenusa. Ilustrándolo a través de una figura, tenemos
donde C es 90°. Para el triángulo rectángulo de muestra, obtener el seno del ángulo A se puede evaluar como
$latex \sin{(A)} = \frac{a}{c}$
donde A es el ángulo, a es su lado opuesto y c es la hipotenusa del triángulo rectángulo de la figura.
Antes de aprender la demostración de la derivada de la función seno, se recomienda aprender el teorema de Pitágoras, Soh-Cah-Toa & Cho-Sha-Cao y el primer principio de los límites como requisitos previos.
Para repasar, cualquier función se puede derivar igualándola al límite de
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{f(x+h)-f(x)}{h}}$$
Supongamos que nos piden obtener la derivada de
$latex f(x) = \sin{(x)}$
tenemos
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{ \sin{(x+h)} – \sin{(x)} }{h}}$$
Analizando nuestra ecuación, podemos observar que el primer término en el numerador del límite es un seno de la suma de dos ángulos x y h. Con esta observación, podemos tratar de aplicar las identidades de suma y diferencia para seno y coseno, también llamadas identidades de Ptolomeo. Aplicando esto, tenemos
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{ \sin{(x+h)} – \sin{(x)} }{h}}$$
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{ (\sin{(x)}\cos{(h)} + \cos{(x)}\sin{(h)}) – \sin{(x)} }{h}}$$
Intentemos reorganizar el numerador.
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{ \sin{(x)}\cos{(h)} – \sin{(x)} + \cos{(x)}\sin{(h)} }{h}}$$
Teniendo en cuenta el primer y segundo términos de nuestro numerador reorganizado, tenemos
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{ \sin{(x)} (\cos{(h)} – 1) + \cos{(x)}\sin{(h)} }{h}}$$
Haciendo algunos arreglos algebraicos, tenemos
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{ \sin{(x)} (-(1-\cos{(h)})) + \cos{(x)}\sin{(h)} }{h}}$$
$$ \frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{ -\sin{(x)} (1-\cos{(h)}) + \cos{(x)}\sin{(h)} }{h}}$$
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} { \left( \frac{ -\sin{(x)} (1-\cos{(h)}) }{h} + \frac{ \cos{(x)}\sin{(h)} }{h} \right) }$$
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} { \frac{ -\sin{(x)} (1-\cos{(h)}) }{h} } + \lim \limits_{h \to 0} { \frac{ \cos{(x)}\sin{(h)} }{h} }$$
Como estamos calculando el límite en términos de h, todas las funciones que no sean h se considerarán constantes. Reorganizando, tenemos
$$\frac{d}{dx} f(x) = -\sin{(x)} \left( \lim \limits_{h \to 0} { \frac{ (1-\cos{(h)}) }{h} } \right) + \cos{(x)} \left( \lim \limits_{h \to 0} { \frac{ \sin{(h)} }{h} } \right)$$
De acuerdo con los límites de las funciones trigonométricas, el límite de la función trigonométrica $latex \sin{(\theta)}$ a $latex \theta$ cuando $latex \theta$ tiende a cero es igual a uno. Lo mismo se puede aplicar a $latex \sin{(h)}$ sobre $latex h$. Aplicando tenemos
$$\frac{d}{dx} f(x) = -\sin{(x)} \left( \lim \limits_{h \to 0} { \frac{ (1-\cos{(h)}) }{h} } \right) + \cos{(x)} \cdot 1$$
$$\frac{d}{dx} f(x) = -\sin{(x)} \left( \lim \limits_{h \to 0} { \frac{ (1-\cos{(h)}) }{h} } \right) + \cos{(x)}$$
Ya hemos evaluado el límite del último término. Sin embargo, el primer término aún es imposible de ser evaluado definitivamente debido al denominador $latex H$. Intentemos usar otra identidad trigonométrica y ver si el truco funcionará.
Podemos intentar usar la identidad del medio ángulo en el numerador del primer término.
$$\frac{d}{dx} f(x) = -\sin{(x)} \left( \lim \limits_{h \to 0} { \frac{ (1-\cos{(h)}) }{h} } \right) + \cos{(x)}$$
$$\frac{d}{dx} f(x) = -\sin{(x)} \left( \lim \limits_{h \to 0} { \frac{ \left(2\sin^{2}{\left(\frac{h}{2}\right)}\right) }{h} } \right) + \cos{(x)}$$
Aplicar las reglas de fracción al primer término y reorganizar algebraicamente una vez más, tenemos,
$$\frac{d}{dx} f(x) = -\sin{(x)} \left( \lim \limits_{h \to 0} { \frac{ \frac{\sin^{2}{\left(\frac{h}{2}\right)}}{1} }{ \frac{h}{2} } }\right) + \cos{(x)}$$
$$\frac{d}{dx} f(x) = -\sin{(x)} \left( \lim \limits_{h \to 0} { \frac{ \sin^{2}{\left(\frac{h}{2}\right)} }{ \frac{h}{2} }} \right) + \cos{(x)}$$
$$\frac{d}{dx} f(x) = -\sin{(x)} \left( \lim \limits_{h \to 0} { \frac{ \sin{\left(\frac{h}{2}\right)} \cdot \sin{\left(\frac{h}{2}\right)} }{ \frac{h}{2} }} \right) + \cos{(x)}$$
$$\frac{d}{dx} f(x) = -\sin{(x)} \left( \lim \limits_{h \to 0} { \sin{\left(\frac{h}{2}\right)} \cdot \left( \frac{ \sin{\left(\frac{h}{2}\right)} }{ \frac{h}{2} } \right) }\right) + \cos{(x)}$$
Tenemos un seno de una variable sobre esa misma variable. En este caso, es $latex \sin{\left(\frac{h}{2}\right)}$ por todo $latex \frac{h}{2}$. Por lo tanto, podemos aplicar nuevamente los límites de las funciones trigonométricas de $latex \frac{\sin{(\theta)}}{\theta}$.
$$\frac{d}{dx} f(x) = -\sin{(x)} \left( \lim \limits_{h \to 0} { \sin{\left(\frac{h}{2}\right)} \cdot 1} \right) + \cos{(x)}$$
Finalmente, hemos logrado evaluar el límite del primer término. Evaluando sustituyendo el valor de aproximación de $latex h$, tenemos
$$\frac{d}{dx} f(x) = -\sin{(x)} \left( \lim \limits_{h \to 0} { \sin{\left(\frac{h}{2}\right)}} \right) + \cos{(x)}$$
$$\frac{d}{dx} f(x) = -\sin{(x)} \left( \lim \limits_{h \to 0} { \sin{\left(\frac{0}{2}\right)}} \right) + \cos{(x)}$$
$$\frac{d}{dx} f(x) = -\sin{(x)} \left( \lim \limits_{h \to 0} { \sin{(0)} }\right) + \cos{(x)}$$
$$\frac{d}{dx} f(x) = -\sin{(x)} \left( \lim \limits_{h \to 0} {0} \right) + \cos{(x)}$$
$$\frac{d}{dx} f(x) = -\sin{(x)} \cdot 0 + \cos{(x)}$$
$$\frac{d}{dx} f(x) = \cos{(x)}$$
Por tanto, la derivada de la función trigonométrica ‘seno’ es:
$$\frac{d}{dx} (\sin{(x)}) = \cos{(x)}$$
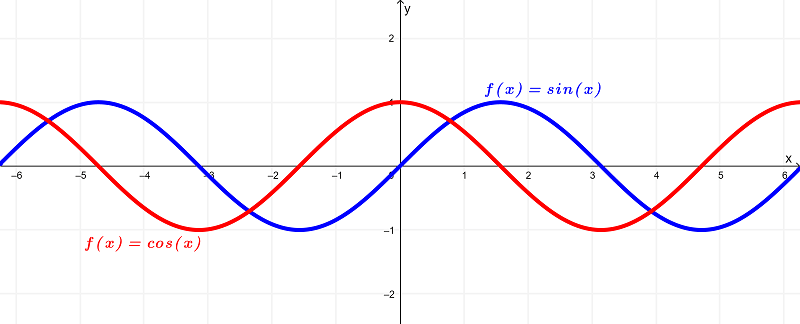
Gráfico de Seno x vs. La derivada del seno x
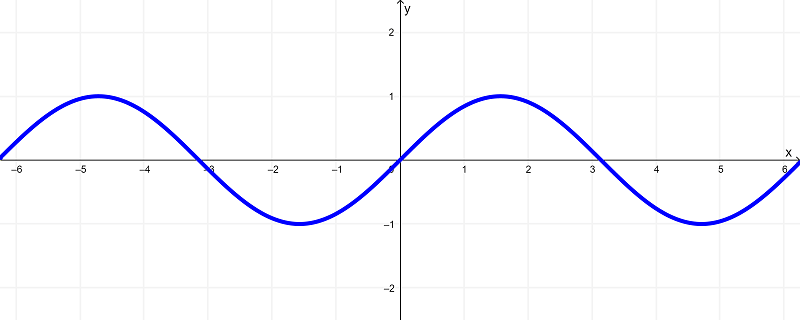
Dada la función
$latex f(x) = \sin{(x)}$
el gráfico se ilustra como
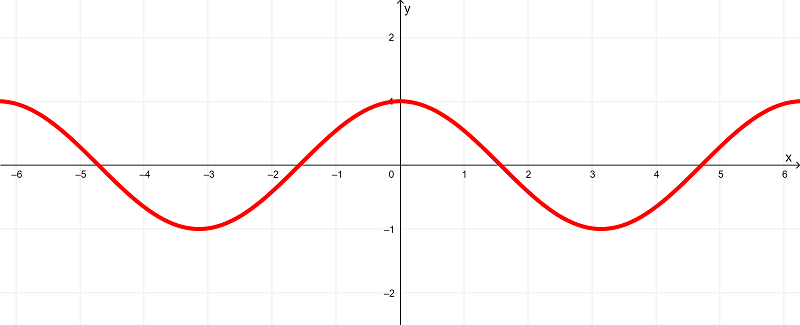
Al derivar a la función $latex f(x) = \sin{(x)}$, obtenemos
$latex f'(x) = \cos{(x)}$
que se ilustra gráficamente como
Comparando sus gráficas, tenemos
Analizando a las gráficas de estas funciones, se puede observar que la función original $latex f(x) = \sin{(x)}$ tiene un dominio de
$latex (-\infty,\infty)$ o todos los números reales
y existe dentro del rango de
$latex [-1,1]$
mientras que la derivada $latex f'(x) = \cos{(x)}$ tiene un dominio de
$latex (-\infty,\infty)$ o todos los números reales
y existe dentro del rango de
$latex [-1,1]$
Ejemplos
Los siguientes son algunos ejemplos sobre cómo derivar funciones seno compuestas.
EJEMPLO 1
¿Cuál es la derivada de $latex f(x) = \sin(4x)$?
Solución
Esta es una función seno compuesta, en donde tenemos al seno de la función interna $latex 4x$. Entonces, podemos encontrar su derivada usando la regla de la cadena.
Escribiendo a la función interna como $latex u=5x$, tenemos $latex f(u)=\sin(u)$ y usando la regla de la cadena, tenemos:
$$\frac{dy}{dx}=\frac{dy}{du} \frac{du}{dx}$$
$$\frac{dy}{dx}=\cos(u) \times 4$$
Sustituyendo $latex u=4x$ de vuelta en la función, tenemos:
$$\frac{dy}{dx}=4\cos(4x)$$
EJEMPLO 2
Encuentra la derivada de la función $latex F(x) = \sin{\left(2x^2+3 \right)}$.
Solución
Dado que es una función seno compuesta, tenemos que usar la regla de la cadena para derivarla.
Usando la sustitución $latex u=2x^2+3$, podemos escribir a la función original como $latex f (u) = \sin(u)$.
Entonces, encontramos la derivada de la función externa, es decir, de la función seno:
$$\frac{d}{du} ( \sin(u) ) = \cos(u)$$
Ahora, encontramos la derivada de la función interna $latex g(x)$ o $latex u$:
$$\frac{d}{dx}(g(x)) = \frac{d}{dx}(2x^2+3)$$
$$\frac{d}{dx}(g(x)) = 4x$$
Luego, aplicamos la regla de la cadena. Es decir, multiplicamos la derivada de la función externa $latex f(u)$ por la derivada de la función interna $latex g(x)$:
$$\frac{dy}{dx} = \frac{d}{du} (f(u)) \cdot \frac{d}{dx} (g(x))$$
$$\frac{dy}{dx} = \cos(u) \cdot 4x$$
Finalmente, substituimos $latex u$ en $latex f'(u)$ y simplificamos:
$$\frac{dy}{dx} = \cos(2x^2+3) \cdot 4x$$
$$\frac{dy}{dx} = 4x\cos(2x^2+3)$$
EJEMPLO 3
Deriva la función $latex f(x) = \sin(\sqrt{x})$
Solución
Tenemos a una función seno compuesta, en donde $latex u=\sqrt{x}$ es la función interna.
Para facilitar la resolución, podemos escribir a $latex u=\sqrt{x}$ como $latex u=x^{\frac{1}{2}}$. Entonces, la derivada $latex \frac{du}{dx}$ es:
$$\frac{du}{dx}=\frac{1}{2}x^{-\frac{1}{2}}$$
Ahora, consideramos que $latex f(u)=\sin(u)$ y usamos la regla de la cadena:
$$\frac{dy}{dx}=\frac{dy}{du} \frac{du}{dx}$$
$$\frac{dy}{dx}=\cos(u) \times \frac{1}{2}x^{-\frac{1}{2}}$$
Usando $latex u=\sqrt{x}$ y simplificando, tenemos:
$$\frac{dy}{dx}=\cos(\sqrt{x}) \times \frac{1}{2}x^{-\frac{1}{2}}$$
$$\frac{dy}{dx}=\frac{1}{2\sqrt{x}}\cos(\sqrt{x})$$
Práctica de derivadas de funciones seno compuestas
Véase también
¿Interesado en aprender más sobre derivadas de funciones trigonométricas? Mira estas páginas:
- Derivada de Coseno, cos(x) – Fórmula, Demostración y Gráficas
- Derivada de Tangente, tan(x) – Fórmula, Demostración y Gráficas
- Derivada de Secante, sec(x) – Fórmula, Demostración y Gráficas
- Derivada de Cosecante, csc(x) – Fórmula, Demostración y Gráficas
- Derivada de Cotangente, cot(x) – Fórmula, Demostración y Gráficas
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
