La Derivada del Coseno es una de las derivadas principales en Cálculo Diferencial (o Cálculo I). La derivada del coseno es igual a menos seno, -sin(x). Esta derivada puede ser demostrada usando límites e identidades trigonométricas.
En este artículo, conoceremos cómo derivar la función trigonométrica coseno. Exploraremos su fórmula, veremos una comparación gráfica de coseno y su derivada y resolveremos algunos ejemplos.
CÁLCULO
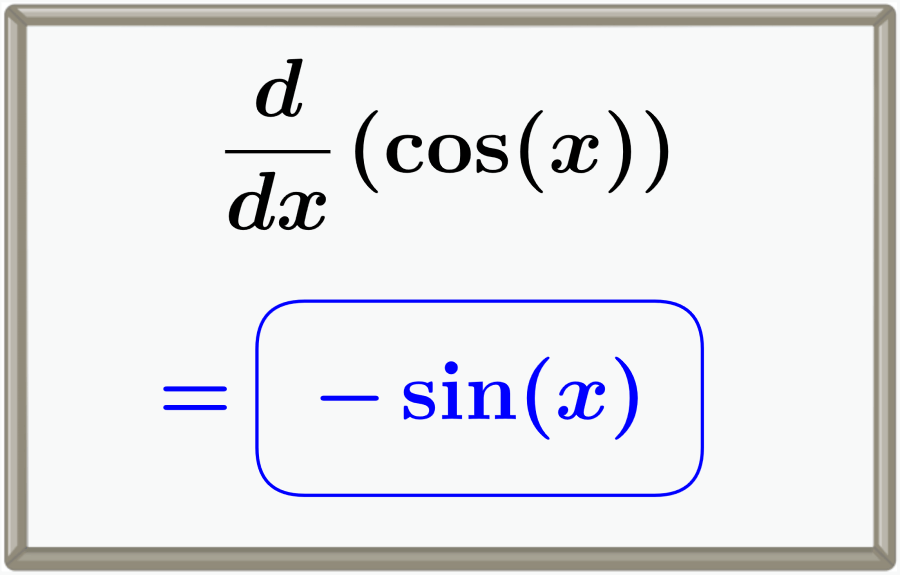
Relevante para…
Aprender sobre la demostración y los gráficos del derivado del coseno.
CÁLCULO
Relevante para…
Aprender sobre la demostración y los gráficos del derivado del coseno.
Demostración de la Derivada de la Función Coseno
La función trigonométrica coseno de un ángulo se define como la relación entre un lado adyacente a un ángulo en un triángulo rectángulo y la hipotenusa. Ilustrándolo a través de una figura, tenemos
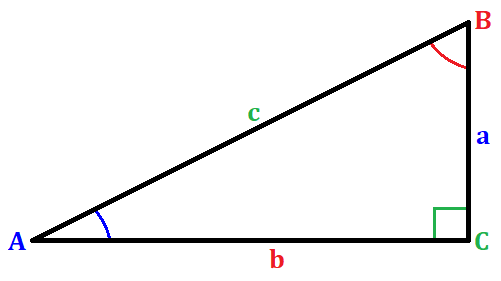
donde C es 90 °. Para el triángulo de la derecha de la muestra, obtener el coseno del ángulo A se puede evaluar como
$latex \cos{(A)} = \frac{b}{c}$
donde A es el ángulo, b es su lado adyacente y c es la hipotenusa del triángulo rectángulo de la figura.
Antes de aprender la prueba de la derivada de la función coseno, se le recomienda aprender el teorema de Pitagorean, Soh-Cah-Toa y Cho-Sha-Cao, y el primer principio de los límites como requisitos previos.
Recordemos que cualquier función se puede derivar igualándola al límite de
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{f(x+h)-f(x)}{h}}$$
Supongamos que nos piden obtener la derivada de
$latex f(x) = \cos{(x)}$
tenemos
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{ \cos{(x+h)} – \cos{(x)} }{h}}$$
Analizando nuestra ecuación, podemos observar que el primer término en el numerador del límite es un coseno de la suma de dos ángulos x y h. Con esta observación, podemos tratar de aplicar las identidades de suma y diferencia para coseno y seno, también llamadas identidades de Ptolomeo. Aplicando esto, tenemos
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{ \cos{(x+h)} – \cos{(x)} }{h}}$$
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{ (\cos{(x)}\cos{(h)} – \sin{(x)}\sin{(h)}) – \cos{(x)} }{h}}$$
Intentemos reorganizar el numerador,
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{ \cos{(x)}\cos{(h)} – \cos{(x)} – \sin{(x)}\sin{(h)} }{h}}$$
Teniendo en cuenta el primer y segundo términos de nuestro numerador reorganizado, tenemos
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{ \cos{(x)}(\cos{(h)} – 1) – \sin{(x)}\sin{(h)}) }{h}}$$
Haciendo algunos arreglos algebraicos, tenemos
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{ \cos{(x)} (-(1-\cos{(h)})) – \sin{(x)}\sin{(h)} }{h}}$$
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{ -\cos{(x)} (1-\cos{(h)}) – \sin{(x)}\sin{(h)} }{h}}$$
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} { \left( \frac{ -\cos{(x)} (1-\cos{(h)}) }{h} – \frac{ \sin{(x)}\sin{(h)} }{h} \right) }$$
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} { \frac{ -\cos{(x)} (1-\cos{(h)}) }{h} } – \lim \limits_{h \to 0} { \frac{ \sin{(x)}\sin{(h)} }{h} }$$
Como estamos calculando el límite en términos de h, todas las funciones que no sean h se considerarán constantes. Reorganizando, tenemos
$$\frac{d}{dx} f(x) = -\cos{(x)} \left( \lim \limits_{h \to 0} { \frac{ (1-\cos{(h)}) }{h} } \right) – \sin{(x)} \left( \lim \limits_{h \to 0} { \frac{ \sin{(h)} }{h} } \right)$$
De acuerdo con los límites de las funciones trigonométricas, el límite de la función trigonométrica $latex \cos(\theta)$ a $latex \theta$ a medida que $latex \theta $ tiende a cero es igual a uno. Lo mismo se puede aplicar a $latex \cos(h)$ sobre $latex H$. Aplicando, tenemos
$$\frac{d}{dx} f(x) = -\cos{(x)} \left( \lim \limits_{h \to 0} { \frac{ (1-\cos{(h)}) }{h} } \right) – \sin{(x)} \cdot 1$$
$$\frac{d}{dx} f(x) = -\cos{(x)} \left( \lim \limits_{h \to 0} { \frac{ (1-\cos{(h)}) }{h} } \right) – \sin{(x)}$$
Ya hemos evaluado el límite del último término. Sin embargo, el primer término aún es imposible de ser evaluado definitivamente debido al denominador $latex H $. Intentemos usar otra identidad trigonométrica y ver si el truco funcionará.
Podemos intentar usar la identidad de medio ángulo en el numerador del primer término.
$$\frac{d}{dx} f(x) = -\cos{(x)} \left( \lim \limits_{h \to 0} { \frac{ (1-\cos{(h)}) }{h} } \right) – \sin{(x)}$$
$$\frac{d}{dx} f(x) = -\cos{(x)} \left( \lim \limits_{h \to 0} { \frac{ \left(2\sin^{2}{\left(\frac{h}{2}\right)}\right) }{h} } \right) – \sin{(x)}$$
Al aplicar las reglas de fracción al primer término y reorganizar algebraicamente una vez más, tenemos,
$$\frac{d}{dx} f(x) = -\cos{(x)} \left( \lim \limits_{h \to 0} { \frac{ \frac{\sin^{2}{\left(\frac{h}{2}\right)}}{1} }{ \frac{h}{2} }} \right) – \sin{(x)}$$
$$\frac{d}{dx} f(x) = -\cos{(x)} \left( \lim \limits_{h \to 0} { \frac{ \sin^{2}{\left(\frac{h}{2}\right)} }{ \frac{h}{2} }} \right) – \sin{(x)}$$
$$\frac{d}{dx} f(x) = -\cos{(x)} \left( \lim \limits_{h \to 0} { \frac{ \sin{\left(\frac{h}{2}\right)} \cdot \sin{\left(\frac{h}{2}\right)} }{ \frac{h}{2} }} \right) – \sin{(x)}$$
$$\frac{d}{dx} f(x) = -\cos{(x)} \left( \lim \limits_{h \to 0} { \sin{\left(\frac{h}{2}\right)} \cdot \left( \frac{ \sin{\left(\frac{h}{2}\right)} }{ \frac{h}{2} } \right) }\right) – \sin{(x)}$$
Como notará una vez más, tenemos un seno de una variable sobre esa misma variable. En este caso, es $latex \sin{\left(\frac{h}{2}\right)}$ sobre $latex \frac{h}{2}$. Por lo tanto, podemos aplicar nuevamente los límites de las funciones trigonométricas de $latex \frac{\sin{(\theta)}}{\theta}$.
$$\frac{d}{dx} f(x) = -\cos{(x)} \left( \lim \limits_{h \to 0} { \sin{\left(\frac{h}{2}\right)} \cdot 1} \right) – \sin{(x)}$$
Finalmente, hemos logrado evaluar el límite del primer término. Evaluando sustituyendo el valor de aproximación de $latex h$, tenemos
$$\frac{d}{dx} f(x) = -\cos{(x)} \left( \lim \limits_{h \to 0} { \sin{\left(\frac{h}{2}\right)} }\right) – \sin{(x)}$$
$$\frac{d}{dx} f(x) = -\cos{(x)} \left( \lim \limits_{h \to 0} { \sin{\left(\frac{0}{2}\right)}} \right) – \sin{(x)}$$
$$\frac{d}{dx} f(x) = -\cos{(x)} \left( \lim \limits_{h \to 0} { \sin{(0)}} \right) – \sin{(x)}$$
$$\frac{d}{dx} f(x) = -\cos{(x)} \left( \lim \limits_{h \to 0} {0} \right) – \sin(x)$$
$$\frac{d}{dx} f(x) = -\cos{(x)} \cdot 0 – \sin{(x)}$$
$$\frac{d}{dx} f(x) = -\sin{(x)}$$
Por tanto, la derivada de la función trigonométrica ‘coseno’ es:
$$\frac{d}{dx} (\cos{(x)}) = -\sin{(x)}$$
Gráfico de coseno de x vs. la derivada del coseno de x
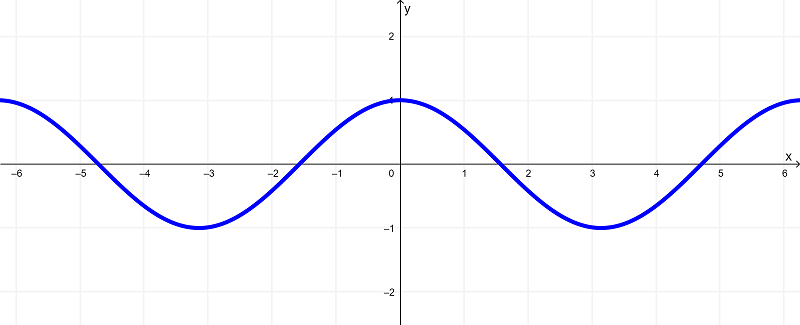
La gráfica de la función
$latex f(x) = \cos{(x)}$
es
Al derivar a la función $latex f(x) = \cos{(x)}$, obtenemos
$latex f'(x) = -\sin{(x)}$
que se ilustra gráficamente como
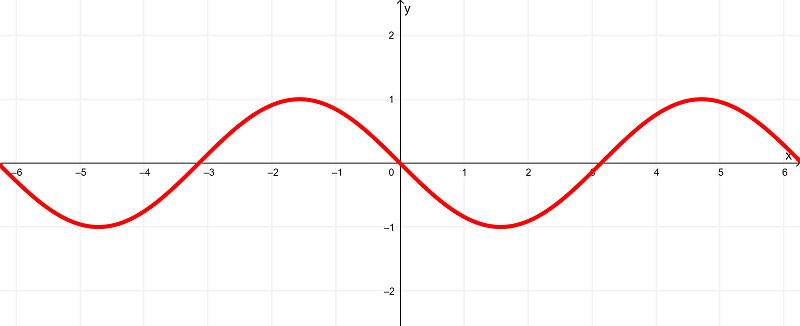
Ilustrando ambas gráficas en una, tenemos
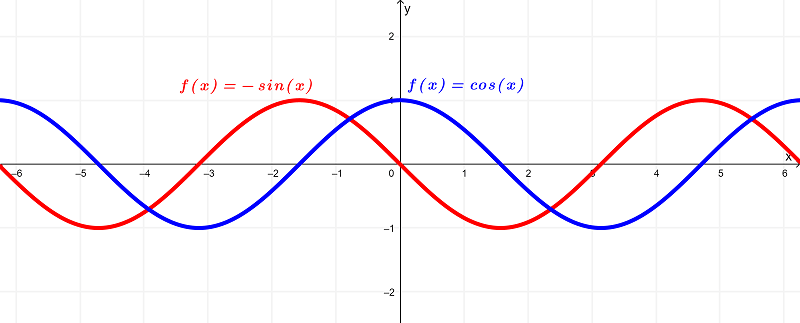
Analizando a estas funciones a través de estas gráficas, vemos que la función original $latex f(x) = \cos(x)$ tiene un dominio de
$latex (-\infty,\infty)$ o todos los números reales
y existe dentro del rango de
$latex [-1,1]$
mientras que la derivada $latex f ‘(x) = -\sin(x)$ tiene un dominio de
$latex (-\infty,\infty)$ o todos los números reales
y existe dentro del rango de
$latex [-1,1]$
Ejemplos
A continuación se muestran algunos ejemplos de cómo encontrar la derivada de una función coseno compuesta usando la regla de la cadena:
EJEMPLO 1
Encuentra la derivada de $latex f(x) = \cos(6x)$
Solución
La función coseno dada es una función compuesta, en donde $latex 6x $ es una función interna. Esto significa que tenemos que usar la regla de la cadena.
Si es que consideramos a $latex u=5x$ como la función interna, tenemos $latex f(u)=\cos(u)$. Entonces, al usar la regla de la cadena, tenemos:
$$\frac{dy}{dx}=\frac{dy}{du} \frac{du}{dx}$$
$$\frac{dy}{dx}=-\sin(u) \times 6$$
Sustituyendo $latex u=6x$ de vuelta en la función, tenemos:
$$\frac{dy}{dx}=-6\sin(6x)$$
EJEMPLO 2
¿Cuál es la derivada de $latex F(x) = \cos(4x^2+5 )$?
Solución
Tenemos una función coseno compuesta, por lo que vamos a usar la regla de la cadena.
Podemos expresar a la función coseno como $latex f (u) = \cos(u)$, donde $latex u = 4x^2+5$.
Entonces, la derivada de la función exterior $latex f(u)$ es:
$$\frac{d}{du} ( \cos(u)) = -\sin(u)$$
Ahora, encontramos la derivada de la función interna $latex g(x)$ o $latex u$:
$$\frac{d}{dx}(g(x)) = \frac{d}{dx}(4x^2+5)$$
$$\frac{d}{dx}(g(x)) = 8x$$
La regla de la cadena nos dice que multiplicamos a la derivada de la función externa $latex f(u)$ por la derivada de la función interna $latex g(x)$. Entonces,
$$\frac{dy}{dx} = \frac{d}{du} (f(u)) \cdot \frac{d}{dx} (g(x))$$
$$\frac{dy}{dx} = -\sin(u) \cdot 8x$$
Por último, substituimos $latex u$ en $latex f'(u)$ y simplificamos:
$$\frac{dy}{dx} = -\sin(4x^2+5) \cdot 8x$$
$$\frac{dy}{dx} = -8x\sin(4x^2+5)$$
EJEMPLO 3
Deriva la función $latex f(x) = \cos(\sqrt{x})$
Solución
Para usar la regla de la cadena, consideramos a $latex u=\sqrt{x}$ como la función interna.
Luego, reescribimos a $latex u=\sqrt{x}$ como $latex u=x^{\frac{1}{2}}$ para facilitar el problema. Entonces, la derivada $latex \frac{du}{dx}$ es:
$$\frac{du}{dx}=\frac{1}{2}x^{-\frac{1}{2}}$$
Ahora, escribimos $latex f(u)=\cos(u)$ y usando la regla de la cadena, tenemos:
$$\frac{dy}{dx}=\frac{dy}{du} \frac{du}{dx}$$
$$\frac{dy}{dx}=-\sin(u) \times \frac{1}{2}x^{-\frac{1}{2}}$$
Usando $latex u=\sqrt{x}$ y simplificando, tenemos:
$$\frac{dy}{dx}=-\sin(\sqrt{x}) \times \frac{1}{2}x^{-\frac{1}{2}}$$
$$\frac{dy}{dx}=-\frac{1}{2\sqrt{x}}\sin(\sqrt{x})$$
Práctica de derivadas de funciones coseno compuestas
Véase también
¿Interesado en aprender más sobre derivadas de funciones trigonométricas? Mira estas páginas:
- Derivada de Seno, sin(x) – Fórmula, Demostración y Gráficas
- Derivada de Tangente, tan(x) – Fórmula, Demostración y Gráficas
- Derivada de Secante, sec(x) – Fórmula, Demostración y Gráficas
- Derivada de Cosecante, csc(x) – Fórmula, Demostración y Gráficas
- Derivada de Cotangente, cot(x) – Fórmula, Demostración y Gráficas
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
