La derivada de la función secante es igual a la secante multiplicada por la tangente, sec(x)tan(x). Esta derivada puede ser demostrada utilizando límites e identidades trigonométricas.
En este artículo, aprenderemos cómo derivar la función trigonométrica secante. Cubriremos una demostración de la derivada, una comparación de gráficas de la secante y su derivada y algunos ejemplos.
CÁLCULO
Relevante para…
Aprender sobre la demostración y gráficas de la derivada de la secante.
CÁLCULO
Relevante para…
Aprender sobre la demostración y gráficas de la derivada de la secante.
Demostración de la derivada de la función secante
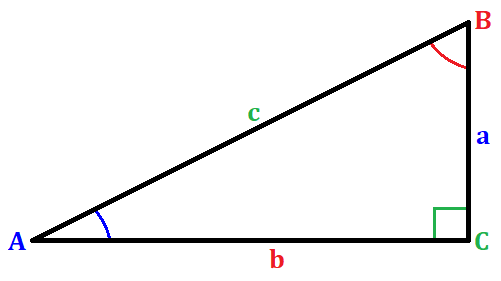
La función trigonométrica secante de un ángulo se define como la relación entre la hipotenusa y el lado adyacente de un ángulo en un triángulo rectángulo. Ilustrándolo a través de una figura, tenemos
donde C es 90 °. Para el triángulo mostrado, obtener el secante del ángulo A se puede evaluar como
$latex \sec{(A)} = \frac{c}{b}$
donde A es el ángulo, C es la hipotenusa, y B es su lado adyacente.
Antes de aprender la prueba de la derivada de la función secante, se le recomienda aprender el teorema de Pitágoras, Soh-Cah-Toa y Cho-Sha-Cao, y el primer principio de los límites como requisitos previos.
Recordemos que cualquier función puede derivarse usando límites de la siguiente manera
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{f(x+h)-f(x)}{h}}$$
Supongamos que se nos pide que obtengamos el derivado de
$latex f(x) = \sec{(x)}$
entonces, tenemos
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{ \sec{(x+h)} – \sec{(x)} }{h}}$$
Analizando nuestra ecuación, podemos observar que tanto el primer como el segundo término en el numerador del límite es una secante de la suma de dos ángulos x y h y una secante del ángulo x. Con esta observación, podemos tratar de aplicar las identidades de relación definitorias para secante y coseno. Aplicando esto, tenemos
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{ \frac{1}{\cos{(x+h)}} – \frac{1}{\cos{(x)}} }{h}}$$
Reordenando algebraicamente aplicando algunas reglas de fracción, tenemos
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{ \frac{ \cos{(x)} – \cos{(x+h)} }{\cos{(x+h)}\cos{(x)}} }{h}}$$
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} { \frac{ \cos{(x)} – \cos{(x+h)} }{h\cos{(x+h)}\cos{(x)}} }$$
Mirando el numerador reorganizado, podemos intentar aplicar las identidades de producto-suma del coseno.
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\left( \frac{ -2\sin{\left(\frac{x+(x+h)}{2}\right)} \sin{\left(\frac{x-(x+h)}{2}\right)} }{h\cos{(x+h)}\cos{(x)}} \right)}$$
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\left( \frac{ -2\sin{\left(\frac{x+x+h}{2}\right)} \sin{\left(\frac{x-x-h}{2}\right)} }{h\cos{(x+h)}\cos{(x)}} \right)}$$
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\left( \frac{ -2\sin{\left(\frac{2x+h}{2}\right)} \sin{\left(\frac{-h}{2}\right)} }{h\cos{(x+h)}\cos{(x)}} \right)}$$
Basado en las identidades trigonométricas de un seno de un ángulo negativo, esto es igual al seno negativo de ese mismo ángulo pero en forma positiva. Aplicando esto al segundo multiplicando del numerador, tenemos
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\left( \frac{ -2\sin{\left(\frac{2x+h}{2}\right)} \cdot \left( -\sin{\left(\frac{h}{2}\right)} \right) }{h\cos{(x+h)}\cos{(x)}} \right)}$$
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\left( \frac{ 2\sin{\left(\frac{2x+h}{2}\right)} \sin{\left(\frac{h}{2}\right)} }{h\cos{(x+h)}\cos{(x)}} \right)}$$
Reordenando algebraicamente y aplicando el límite del producto de dos funciones, tenemos
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\left( \frac{ \sin{\left(\frac{2x+h}{2}\right)} \cdot 2\sin{\left(\frac{h}{2}\right)} }{\cos{(x+h)}\cos{(x)} \cdot h} \right)}$$
$$ \frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\left( \frac{\sin{\left(\frac{2x+h}{2}\right)} }{ \cos{(x+h)}\cos{(x)} } \cdot \frac{ 2\sin{\left(\frac{h}{2}\right)} }{h} \right)}$$
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\left( \frac{\sin{\left(\frac{2x+h}{2}\right)} }{ \cos{(x+h)}\cos{(x)} } \right)} \cdot \lim \limits_{h \to 0} {\left( \frac{ 2\sin{\left(\frac{h}{2}\right)} }{h} \right)}$$
Aplicando algunas reglas de fracciones a la segunda multiplicando, tenemos
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\left( \frac{\sin{\left(\frac{2x+h}{2}\right)} }{ \cos{(x+h)}\cos{(x)} } \right)} \cdot \lim \limits_{h \to 0} {\left( \frac{ \sin{\left(\frac{h}{2}\right)} }{ \frac{h}{2} } \right)}$$
De acuerdo con los límites de las funciones trigonométricas, el límite de la función trigonométrica $latex \sin{(\theta)}$ a $latex \theta$ cuando $latex \theta$ tiende a cero es igual a uno. Lo mismo se puede aplicar a $latex \sin{\left(\frac{h}{2}\right)}$ sobre $latex \frac{h}{2}$. Aplicando tenemos
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\left( \frac{\sin{\left(\frac{2x+h}{2}\right)} }{ \cos{(x+h)}\cos{(x)} } \right)} \cdot \lim \limits_{h \to 0} {1}$$
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\left( \frac{\sin{\left(\frac{2x+h}{2}\right)} }{ \cos{(x+h)}\cos{(x)} } \right)}$$
Finalmente, hemos hecho posible evaluar el límite de lo que queda en la ecuación. Evaluando sustituyendo el valor de aproximación de $latex h$, tenemos
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\left( \frac{\sin{\left(\frac{2x+(0)}{2}\right)} }{ \cos{(x+(0))}\cos{(x)} } \right)}$$
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\left( \frac{\sin{\left(\frac{2x}{2}\right)} }{ \cos{(x)}\cos{(x)} } \right)}$$
$$\frac{d}{dx} f(x) = \frac{\sin{(x)} }{ \cos{(x)}\cos{(x)} }$$
Aplicando algunas identidades trigonométricas para simplificar la fórmula derivada mediante el uso de identidades de relaciones definidas, tenemos
$$\frac{d}{dx} f(x) = \frac{ \sin{(x)} }{ \cos{(x)} } \cdot \frac{1}{\cos{(x)}} $$
$$\frac{d}{dx} f(x) = \tan{(x)} \cdot \sec{(x)} $$
$$\frac{d}{dx} f(x) = \sec{(x)} \tan{(x)}$$
Por tanto, la derivada de la función trigonométrica ‘secante’ es:
$$\frac{d}{dx} (\sec{(x)}) = \sec{(x)} \tan{(x)}$$
Gráfica de la secante de x vs. la derivada de la secante de x
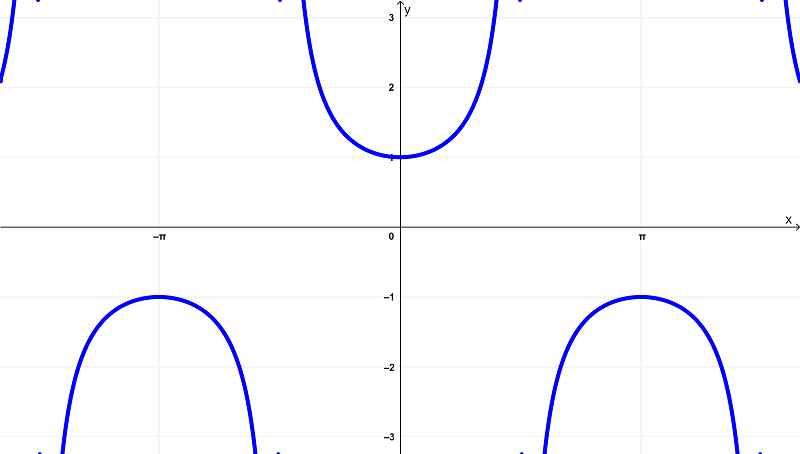
La gráfica de la función
$latex f(x) = \sec{(x)}$
es
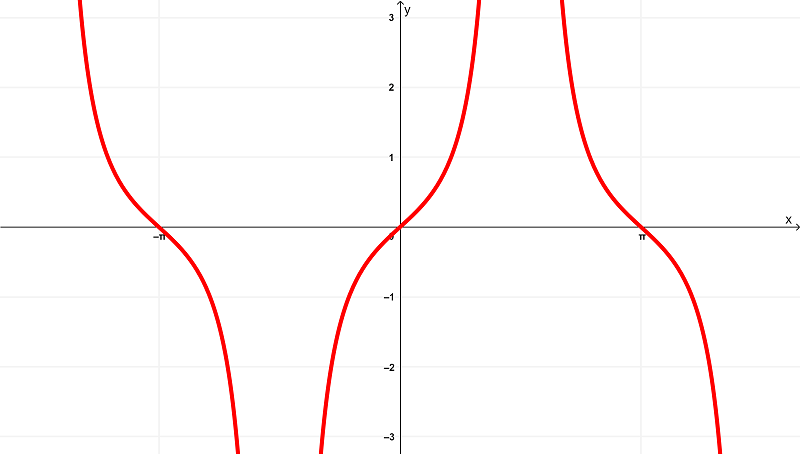
Derivando $latex f (x) = \sec(x)$, obtenemos
$latex f'(x) = \sec{(x)}\tan{(x)}$
que se ilustra gráficamente como
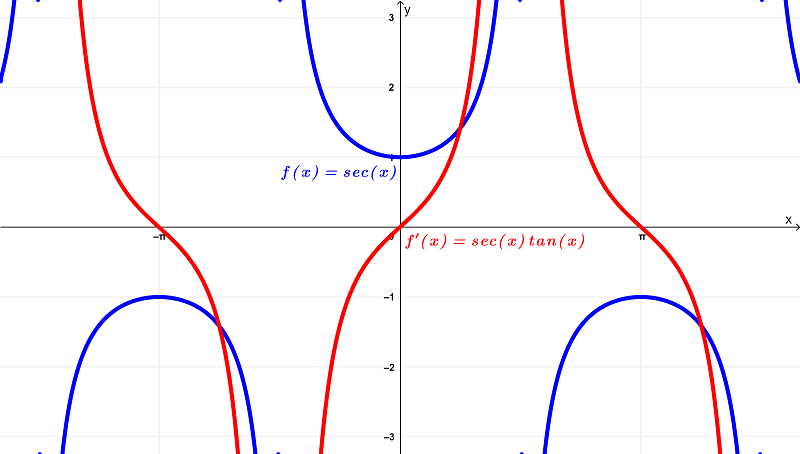
Haciendo una comparación de sus gráficas, tenemos
Podemos observar que la función original $latex f(x) = \sec{(x)}$ tiene un dominio de
$$\left(-\frac{3\pi}{2},-\frac{\pi}{2}\right) \cup \left(-\frac{\pi}{2},\frac{\pi}{2}\right) \cup \left(\frac{\pi}{2},\frac{3\pi}{2}\right)$$
dentro de los intervalos finitos de
$latex \left(-\frac{3\pi}{2},\frac{3\pi}{2}\right)$
y existe dentro del rango de
$latex (-\infty,-1] \cup [1,\infty)$
mientras que la derivada $latex f ‘(x) = \sec(x) \tan(x) $ tiene un dominio de
$$ \left(-\frac{3\pi}{2},-\frac{\pi}{2}\right) \cup \left(-\frac{\pi}{2},\frac{\pi}{2}\right) \cup \left(\frac{\pi}{2},\frac{3\pi}{2}\right)$$
dentro de los intervalos finitos de
$latex \left(-\frac{3\pi}{2},\frac{3\pi}{2}\right)$
y existe dentro del rango de
$latex (-\infty,\infty)$ o todos los números reales
Ejemplos
Los siguientes son algunos ejemplos de cómo derivar funciones secante compuestas con la regla de la cadena.
EJEMPLO 1
Encuentra la derivada de $latex f(x) = \sec(10x)$.
Solución
La función secante dada es una función compuesta, ya que es una secante de la función $latex 10x$. Entonces, vamos a usar la regla de la cadena.
Si es que $latex u=10x$ es la función interna, tenemos $latex f(u)=\sec(u)$ y usando la regla de la cadena, tenemos:
$$\frac{dy}{dx}=\frac{dy}{du} \frac{du}{dx}$$
$$\frac{dy}{dx}=\sec(u)\tan(u) \times 10$$
Finalmente, sustituimos $latex u=10x$ de vuelta en la función y tenemos:
$$\frac{dy}{dx}=10\sec(10x)\tan(10x)$$
EJEMPLO 2
Encuentra la derivada de $latex F(x) = \sec(8x^2-4)$
Solución
Como tenemos una función secante compuesta, tenemos que usar la regla de la cadena para derivar.
Empezamos expresando a la función secante como $latex f (u) = \sec(u)$, donde $latex u = 8x^2-4$.
Luego, calculamos la derivada de la función exterior $latex f(u)$, es decir, la derivada de la función secante en términos de $latex u$:
$$\frac{d}{du} ( \sec{(u)} ) = \sec(u)\tan(u)$$
Ahora, calculamos la derivada de la función interna $latex g(x)$ o $latex u$:
$$\frac{d}{dx}(g(x)) = \frac{d}{dx}(8x^2-4)$$
$$\frac{d}{dx}(g(x)) = 16x$$
Usando la regla de la cadena, multiplicamos la derivada de la función externa por la derivada de la función interna:
$$\frac{dy}{dx} = \frac{d}{du} (f(u)) \cdot \frac{d}{dx} (g(x))$$
$$\frac{dy}{dx} = \sec(u)\tan(u) \cdot 16x$$
Por último, substituimos $latex u=8x^2-4$ de vuelta:
$$\frac{dy}{dx} = \sec(8x^2-4)\tan(8x^2-4) \cdot 16x$$
$$\frac{dy}{dx} = 16x\sec(8x^2-4)\tan(8x^2-4)$$
EJEMPLO 3
¿Cuál es la derivada de $latex f(x) = \sec(\sqrt{x})$?
Solución
Podemos derivar a esta función al considerar a $latex u=\sqrt{x}$ como la función interna.
Entonces, empezamos escribiendo a $latex u=\sqrt{x}$ como $latex u=x^{\frac{1}{2}}$ para encontrar la derivada de $latex u$ en términos de $latex x$:
$$\frac{du}{dx}=\frac{1}{2}x^{-\frac{1}{2}}$$
Ahora, consideramos que $latex f(u)=\sec(u)$ y usamos la regla de la cadena:
$$\frac{dy}{dx}=\frac{dy}{du} \frac{du}{dx}$$
$$\frac{dy}{dx}=\sec(u)\tan(u) \times \frac{1}{2}x^{-\frac{1}{2}}$$
Sustituyendo $latex u=\sqrt{x}$ de vuelta y simplificando, tenemos:
$$\frac{dy}{dx}=\sec(\sqrt{x})\tan(\sqrt{x}) \times \frac{1}{2}x^{-\frac{1}{2}}$$
$$\frac{dy}{dx}=\frac{1}{2\sqrt{x}}\sec(\sqrt{x})\tan(\sqrt{x})$$
Práctica de derivadas de funciones secante compuestas
Véase también
¿Interesado en aprender más sobre derivadas de funciones trigonométricas? Mira estas páginas:
- Derivada de Seno, sin(x) – Fórmula, Demostración y Gráficas
- Derivada de Coseno, cos(x) – Fórmula, Demostración y Gráficas
- Derivada de Tangente, tan(x) – Fórmula, Demostración y Gráficas
- Derivada de Cosecante, csc(x) – Fórmula, Demostración y Gráficas
- Derivada de Cotangente, cot(x) – Fórmula, Demostración y Gráficas
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
