La derivada de la tangente es una de las primeras funciones trascendentales introducidas en el cálculo diferencial (o cálculo I). La derivada de la función tangente es igual a secante al cuadrado, sec2(x). Podemos demostrar esta derivada utilizando límites e identidades trigonométricas.
En este artículo, discutiremos cómo derivar la función trigonométrica tangente. Cubriremos breves fundamentos, su fórmula, una comparación gráfica de tangente y su derivada, una prueba, métodos para derivar y algunos ejemplos.
CÁLCULO
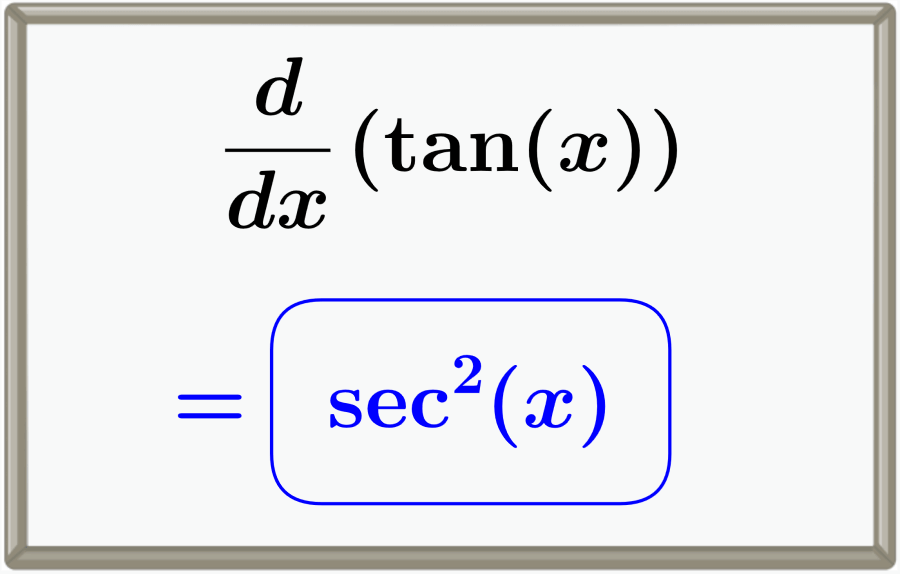
Relevante para…
Aprender sobre la demostración y las gráficas de la derivada de la tangente.
CÁLCULO
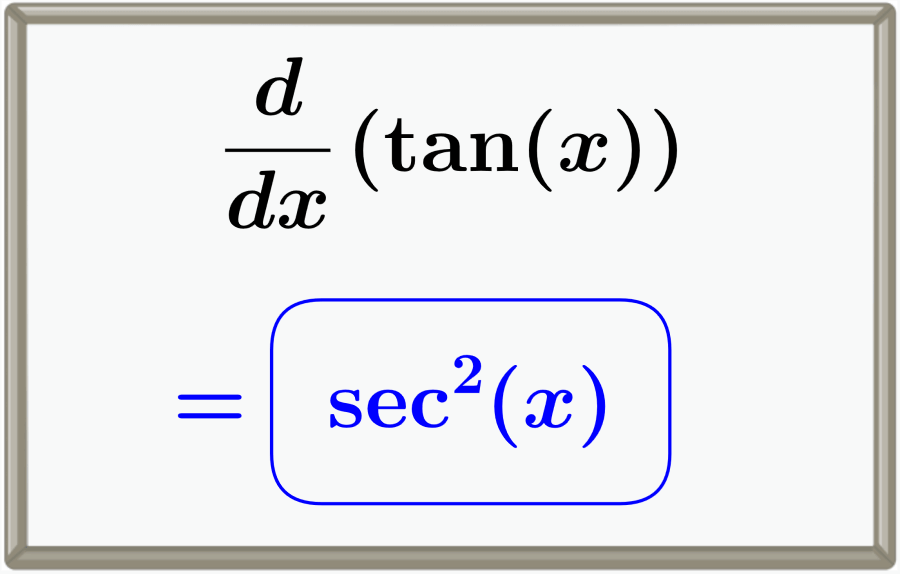
Relevante para…
Aprender sobre la demostración y las gráficas de la derivada de la tangente.
Demostración de la Derivada de la Función Tangente usando límites
La función trigonométrica tangente de un ángulo se define como la relación entre el lado opuesto y el lado adyacente de un ángulo en un triángulo rectángulo. Ilustrándolo a través de una figura, tenemos
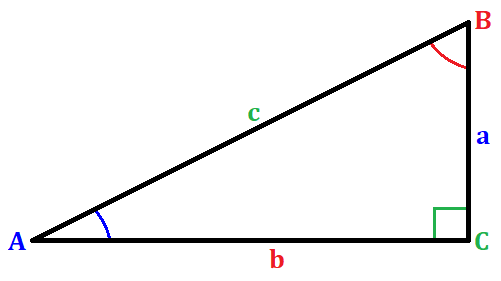
donde C es 90°. Por lo tanto, obtener la tangente del ángulo A se puede evaluar como
$latex \tan{(A)} = \frac{a}{b}$
Antes de aprender la demostración de la derivada de la función tangente, se recomienda aprender el teorema de Pitágoras, Soh-Cah-Toa & Cho-Sha-Cao y el primer principio de los límites como requisitos previos.
Recordemos que cualquier función puede derivarse equiparándola hasta el límite de
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{f(x+h)-f(x)}{h}}$$
Supongamos que nos piden obtener la derivada de
$latex f(x) = \tan{(x)}$
entonces, tenemos
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{ \tan{(x+h)} – \tan{(x)} }{h}}$$
Con esta ecuación, todavía no es posible expresar el límite debido al denominador h donde si se sustituye por cero, quedará indefinido. Por lo tanto, podemos comprobar si puede ser útil aplicar algunas identidades trigonométricas.
Analizando nuestra ecuación, podemos observar que tanto el primer como el segundo término en el numerador del límite es una tangente de la suma de dos ángulos x y h y una tangente del ángulo x. Con esta observación, podemos intentar aplicar las identidades de relación definitorias para tangente, seno y coseno. Aplicando esto, tenemos
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{ \frac{\sin{(x+h)}}{\cos{(x+h)}} – \frac{\sin{(x)}}{\cos{(x)}} }{h}}$$
Reordenando algebraicamente aplicando algunas reglas de fracción, tenemos
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{ \frac{\sin{(x+h)}\cos{(x)} – \cos{(x+h)}\sin{(x)}}{\cos{(x+h)}\cos{(x)}} }{h}}$$
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{ \sin{(x+h)}\cos{(x)} – \cos{(x+h)}\sin{(x)} }{h\cos{(x+h)}\cos{(x)}}}$$
Mirando el numerador reorganizado, podemos intentar aplicar las identidades de suma y diferencia para el seno y el coseno, también llamadas identidades de Ptolomeo.
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{ \sin{(x+h-x)} }{h\cos{(x+h)}\cos{(x)}}}$$
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{ \sin{(h)} }{h\cos{(x+h)}\cos{(x)}}}$$
Reordenando aplicando el límite del producto de dos funciones, tenemos
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\left( \frac{ \sin{(h)} }{h} \cdot \frac{1}{\cos{(x+h)}\cos{(x)}} \right)}$$
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\left( \frac{ \sin{(h)} }{h} \right)} \cdot \lim \limits_{h \to 0} {\left(\frac{1}{\cos{(x+h)}\cos{(x)}} \right)}$$
De acuerdo con los límites de las funciones trigonométricas, el límite de la función trigonométrica $latex \sin{(\theta)}$ a $latex \theta$ cuando $latex \theta$ tiende a cero es igual a uno. Lo mismo se puede aplicar a $latex \sin{(h)}$ sobre $latex h$. Aplicando tenemos
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {1} \cdot \lim \limits_{h \to 0} {\left(\frac{1}{\cos{(x+h)}\cos{(x)}} \right)}$$
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\left(\frac{1}{\cos{(x+h)}\cos{(x)}} \right)}$$
Finalmente, hemos hecho posible evaluar el límite de lo que queda en la ecuación. Evaluando sustituyendo el valor de aproximación de $latex h$, tenemos
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\left(\frac{1}{\cos{(x+h)}\cos{(x)}} \right)}$$
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\left(\frac{1}{\cos{(x+(0))}\cos{(x)}} \right)}$$
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\left(\frac{1}{\cos{(x)}\cos{(x)}} \right)}$$
$$ \frac{d}{dx} f(x) = \frac{1}{\cos{(x)}\cos{(x)}}$$
Sabemos que mediante las identidades, el recíproco del coseno de la función trigonométrica es secante. Aplicando, tenemos
$$\frac{d}{dx} f(x) = \frac{1}{\cos{(x)}} \cdot \frac{1}{\cos{(x)}}$$
$$\frac{d}{dx} f(x) = \sec{(x)} \cdot \sec{(x)}$$
$$\frac{d}{dx} f(x) = \sec^{2}{(x)}$$
Por tanto, la derivada de la función trigonométrica ‘tangente’ es:
$$\frac{d}{dx} (\tan{(x)}) = \sec^{2}{(x)}$$
Gráfica de Tangente de x vs. la derivada de la tangente de x
Dada la función
$latex f(x) = \tan{(x)}$
su gráfica es
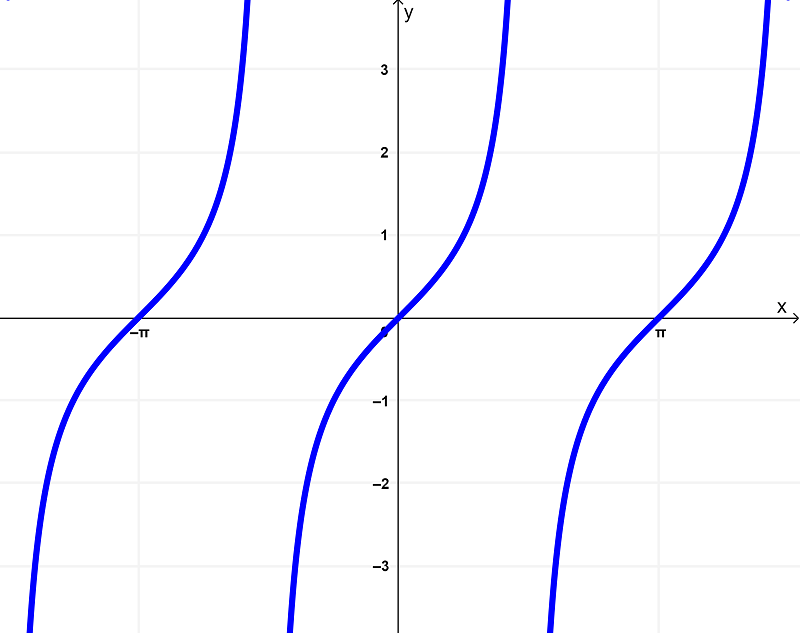
Y como ya sabemos, al derivar $latex f(x) = \tan{(x)}$, obtenemos
$latex f'(x) = \sec^{2}{(x)}$
que se ilustra gráficamente como
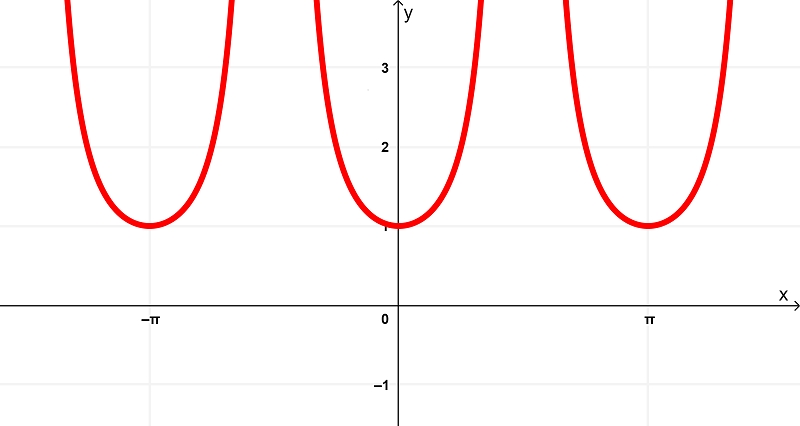
Ilustrando ambos gráficos en uno, tenemos
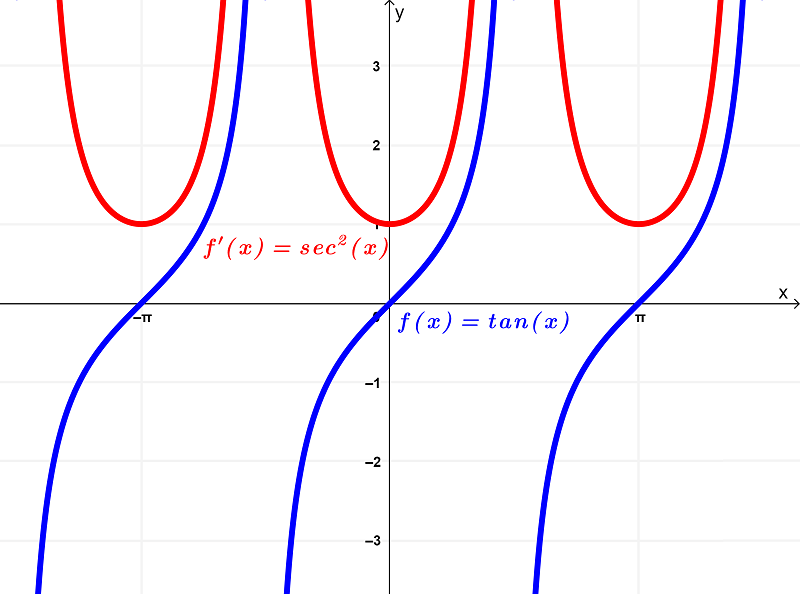
Analizando las diferencias de estas funciones a través de estas gráficas, puedes observar que la función original $latex f(x) = \tan{(x)}$ tiene un dominio de
$$\left(-\frac{3\pi}{2},-\frac{\pi}{2}\right) \cup \left(-\frac{\pi}{2},\frac{\pi}{2}\right) \cup \left(\frac{\pi}{2},\frac{3\pi}{2}\right)$$
dentro de los intervalos finitos de
$latex \left(-\frac{3\pi}{2},\frac{3\pi}{2}\right)$
y existe dentro del rango de
$latex (-\infty,\infty)$ o todos los números reales
mientras que la derivada $latex f ‘(x) = \sec^{2}{(x)}$ tiene un dominio de
$$\left(-\frac{3\pi}{2},-\frac{\pi}{2}\right) \cup \left(-\frac{\pi}{2},\frac{\pi}{2}\right) \cup \left(\frac{\pi}{2},\frac{3\pi}{2}\right)$$
dentro de los intervalos finitos de
$latex \left(-\frac{3\pi}{2},\frac{3\pi}{2}\right)$
y existe dentro del rango de
$latex [1,\infty)$ or $latex y \geq 1$
Ejemplos de derivadas de funciones tangente compuestas
A continuación se muestran algunos ejemplos del uso de la regla de la cadena derivar una función tangente compuesta.
EJEMPLO 1
Deriva: $latex f(x) = \tan(5x)$
Solución
Analizando la función tangente dada, vemos que es una tangente de la función $latex 5x$. Entonces, tenemos que usar la regla de la cadena.
Podemos considerar a $latex u=5x$ como la función interna. Entonces, tenemos $latex f(u)=\tan(u)$ y usando la regla de la cadena, tenemos:
$$\frac{dy}{dx}=\frac{dy}{du} \frac{du}{dx}$$
$$\frac{dy}{dx}=\sec^2(u) \times 5$$
Sustituyendo $latex u=5x$ de vuelta en la función, tenemos:
$$\frac{dy}{dx}=5\sec^2(5x)$$
EJEMPLO 2
Deriva: $latex F(x) = \tan{\left(3x^2+6 \right)}$
Solución
La regla de la cadena tiene que ser usada para derivar esta función.
Expresamos a la función tangente como $latex f (u) = \tan(u)$, donde $latex u = 3x^2+6$.
Ahora, obtenemos la derivada de la función exterior $latex f(u)$, que debe usar la derivada de la función tangente, en términos de $latex u$.
$$\frac{d}{du} ( \tan{(u)} ) = \sec^{2}(u)$$
Luego, obtenemos la derivada de la función interna $latex g(x)$ o $latex u$:
$$\frac{d}{dx}(g(x)) = \frac{d}{dx}(3x^2+6)$$
$$\frac{d}{dx}(g(x)) = 6x$$
Aplique la fórmula básica de la regla de la cadena multiplicando algebraicamente la derivada de la función externa $latex f(u)$ por la derivada de la función interna $latex g(x)$
$$\frac{dy}{dx} = \frac{d}{du} (f(u)) \cdot \frac{d}{dx} (g(x))$$
$$\frac{dy}{dx} = \sec^{2}{(u)} \cdot 6x$$
Por último, substituye $latex u$ en $latex f'(u)$ y simplifica:
$$\frac{dy}{dx} = \sec^{2}{(3x^2+6)} \cdot 6x$$
$$\frac{dy}{dx} = 6x\sec^{2}{(3x^2+6)}$$
$latex F'(x) = 6x\sec^{2}{(3(x^2+2))}$
EJEMPLO 3
Encuentra la derivada de $latex f(x) = \tan(\sqrt{x})$
Solución
En este caso, tenemos a la función raíz cuadrada como la función interna de la tangente. Podemos considerar a $latex u=\sqrt{x}$ como la función interna.
Además, si es que escribimos a $latex u=\sqrt{x}$ como $latex u=x^{\frac{1}{2}}$, la derivada $latex \frac{du}{dx}$ es:
$$\frac{du}{dx}=\frac{1}{2}x^{-\frac{1}{2}}$$
Escribiendo $latex f(u)=\tan(u)$ y usando la regla de la cadena, tenemos:
$$\frac{dy}{dx}=\frac{dy}{du} \frac{du}{dx}$$
$$\frac{dy}{dx}=\sec^2(u) \times \frac{1}{2}x^{-\frac{1}{2}}$$
Usando $latex u=\sqrt{x}$ y simplificando, tenemos:
$$\frac{dy}{dx}=\sec^2(\sqrt{x}) \times \frac{1}{2}x^{-\frac{1}{2}}$$
$$\frac{dy}{dx}=\frac{1}{2\sqrt{x}}\sec^2(\sqrt{x})$$
Práctica de derivadas de funciones tangente compuestas
Véase también
¿Interesado en aprender más sobre derivadas de funciones trigonométricas? Mira estas páginas:
- Derivada de Seno, sin(x) – Fórmula, Demostración y Gráficas
- Derivada de Coseno, cos(x) – Fórmula, Demostración y Gráficas
- Derivada de Secante, sec(x) – Fórmula, Demostración y Gráficas
- Derivada de Cosecante, csc(x) – Fórmula, Demostración y Gráficas
- Derivada de Cotangente, cot(x) – Fórmula, Demostración y Gráficas
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
