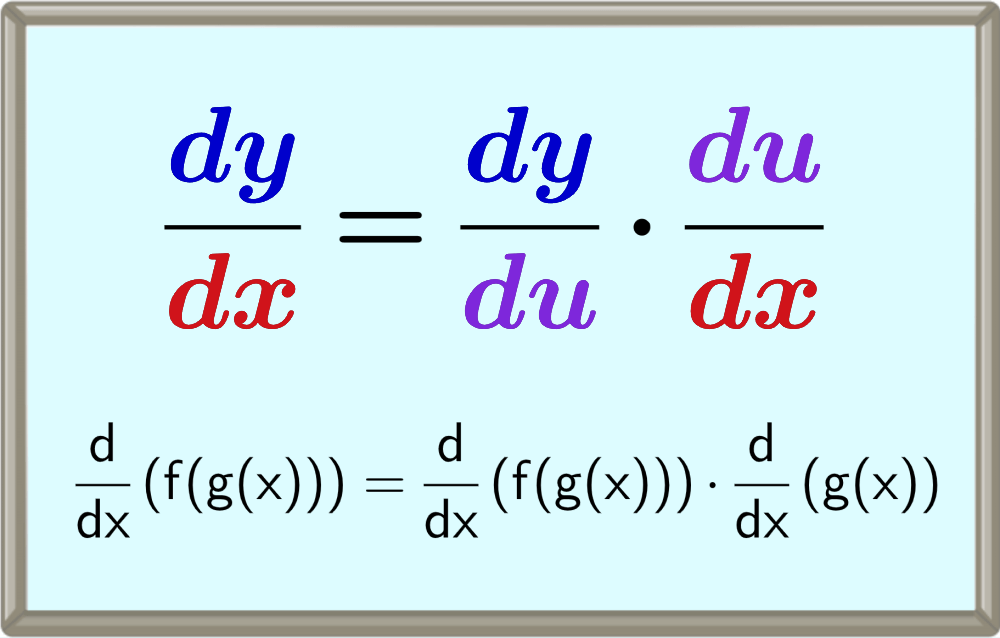La Regla de la Cadena es una de las técnicas de derivadas más comunes aplicadas en Cálculo Diferencial (o Cálculo I). Se utiliza para derivar una composición de funciones. La regla de la cadena se puede demostrar usando uno de los pilares del cálculo, que son los límites.
En este artículo, exploraremos todo sobre la regla de la cadena. Cubriremos su definición, fórmula, demostraciones y aplicaciones. También veremos algunos ejemplos y problemas de práctica para aplicar los principios de la regla de la cadena.
La regla de la cadena y su fórmula
¿Qué es la regla de la cadena?
La regla de la cadena se define como la derivada de una composición de al menos dos tipos diferentes de funciones como:
$$y’ = \frac{d}{dx}[f \left( g(x) \right)]$$
donde g(x) es un dominio de la función f(u).
También podemos llamar a la función f como la función externa y a la función g como la función interna. En esta composición, f(x) y g(x) deben ser dos tipos diferentes de funciones que no pueden evaluarse algebraicamente en un solo tipo de función.
Recuerda que una composición de funciones puede considerarse como una función dentro de otra función o como una función de otra función.
La fórmula de la regla de la cadena
La fórmula de la regla de la cadena se puede expresar verbalmente como la derivada de la función externa f multiplicada por la derivada de la función interna g. La función interna g es el dominio de la derivada de la función externa f.
La fórmula de la regla de la cadena se puede ilustrar como:
$$\frac{d}{dx} (f(g(x))) = \frac{d}{dx} (f(g(x))) \cdot \frac{d}{dx}(g(x))$$
donde derivamos f(g(x)) usando el método de derivada de la función f y usando g(x) como el dominio de la función f y luego multiplicando la derivada de la función f por la derivada de g(x).
En otra forma, también se puede ilustrar como:
$$\frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx}$$
en donde
- $latex f(u) =$ la función externa
- $latex u = g(x)$, el dominio de la función externa $latex f(u)$
- $latex \frac{dy}{du} =$ la derivada de la función externa $latex f(u)$ en términos de $latex u$
- $latex \frac{du}{dx} =$ la derivada de la función interna $latex g(x)$ en términos de $latex x$
Para obtener más información sobre la demostración de la regla de la cadena usando límites, visita nuestro artículo sobre la demostración de la regla de la cadena.
Cómo usar la regla de la cadena, un tutorial paso a paso
Supongamos que tenemos que derivar
$latex H(x) = \sin{(x^3)}$
Como puedes observar, esta función dada puede considerarse una función compuesta. Por lo tanto, podemos usar la fórmula de la regla de la cadena para derivar este problema.
1. Escribimos la fórmula de la regla de la cadena como referencia:
$$\frac{d}{dx} (H(x)) = \frac{d}{dx} \left(f(g(x)) \right) \cdot \frac{d}{x}(g(x))$$
Puedes usar cualquier forma de la fórmula de la regla de la cadena.
2. Identificar a las funciones externa e interna.
Si es que consideramos a la función interna como $latex g(x) = u=x^3$, entonces
$latex f(g(x)) = f(u)$
$latex f(u) = \sin{(u)}$
3. Aplicar la fórmula de la regla de la cadena.
$$\frac{d}{dx} H(x) = \frac{d}{du}(f(u)) \cdot \frac{d}{dx}(g(x))$$
$$\frac{d}{dx} H(x) = \frac{d}{du}(\sin{(u)}) \cdot \frac{d}{dx}(x^3)$$
$$\frac{d}{dx} H(x) = (\cos{(u)}) \cdot (3x^2)$$
4. Sustituye la función interna $latex g(x)=u=x^3$ en la ecuación derivada:
$$\frac{d}{dx} H(x) = (\cos{(x^3)}) \cdot (3x^2)$$
5. Simplifica la derivada obtenida:
$$\frac{d}{dx} H(x) = 3x^2 \cdot \cos{(x^3)}$$
$latex H'(x) = 3x^2 \cos{(x^3)}$
Regla de la cadena – Ejemplos con respuestas
EJEMPLO 1
Deriva la siguiente función:
$latex H(x) = (12x+6)^{24}$
Solución
Paso 1: Escribe la fórmula de la regla de la cadena como referencia:
$$\frac{d}{dx} (H(x)) = \frac{d}{dx} \left(f(g(x)) \right) \cdot \frac{d}{x}(g(x))$$
Paso 2: Al reconocer las dos funciones, tenemos
Si es que $latex g(x) = u=12x+6$, entonces
$latex f(g(x)) = f(u)$
$latex f(u) = u^{24}$
Paso 3: Apliquemos ahora la fórmula de la regla de la cadena:
$$\frac{d}{dx} H(x) = \frac{d}{du}(f(u)) \cdot \frac{d}{dx}(g(x))$$
$$\frac{d}{dx} H(x) = \frac{d}{du}(u^{24}) \cdot \frac{d}{dx}(12x+6)$$
$$\frac{d}{dx} H(x) = (24u^{23}) \cdot (12)$$
Paso 4: Sustituye la función interna $latex g(x)$ en la ecuación derivada:
$$\frac{d}{dx} H(x) = (24(12x+6)^{23}) \cdot (12)$$
Paso 5: Simplifica algebraicamente:
$$\frac{d}{dx} H(x) = 288 \cdot (12x+6)^{23}$$
$latex H'(x) = 288(12x+6)^{23}$
EJEMPLO 2
Encuentra la derivada de la función dada.
$latex f(x) = \sqrt[12]{6x-3}$
Solución
Paso 1: Enumera la fórmula de la regla de la cadena como referencia:
$$\frac{d}{dx} (H(x)) = \frac{d}{dx} \left(f(g(x)) \right) \cdot \frac{d}{x}(g(x))$$
Paso 2: Si es que $latex g(x) = u=6x-3$, entonces
$latex f(g(x)) = f(u)$
$latex f(u) = \sqrt[12]{u}$
$latex f(u) = u^{\frac{1}{12}}$
Paso 3: Apliquemos ahora la fórmula de la regla de la cadena:
$$\frac{d}{dx} H(x) = \frac{d}{du}(f(u)) \cdot \frac{d}{dx}(g(x))$$
$$\frac{d}{dx} H(x) = \frac{d}{du}(u^{\frac{1}{12}}) \cdot \frac{d}{dx}(6x-3)$$
$$\frac{d}{dx} H(x) = \left(\frac{1}{12}u^{-\frac{11}{12}} \right) \cdot (6)$$
Paso 4: Sustituye la función interna $latex g(x)=u=6x-3$ en la ecuación derivada:
$$\frac{d}{dx} H(x) = \left(\frac{1}{12} \cdot (6x-3)^{-\frac{11}{12}} \right) \cdot (6)$$
Paso 5: Simplifica algebraicamente:
$$\frac{d}{dx} H(x) = \frac{6}{12 \cdot (6x-3)^{\frac{11}{12}}}$$
$$\frac{d}{dx} H(x) = \frac{1}{2 \cdot (6x-3)^{\frac{11}{12}}}$$
$$H'(x) = \frac{1}{2 \sqrt[12]{(6x-3)^{11}}}$$
en forma radical
EJEMPLO 3
Deriva la siguiente función:
$latex \cos{(12x^2+6x-3)}$
Solución
Paso 1: Empezamos con la fórmula de la regla de la cadena:
$$\frac{d}{dx} (H(x)) = \frac{d}{dx} \left(f(g(x)) \right) \cdot \frac{d}{x}(g(x))$$
Paso 2: En este ejemplo, tenemos $latex g(x) = u=12x^2+6x-3$, entonces
$latex f(g(x)) = f(u)$
$latex f(u) = \cos{(u)}$
Paso 3: Apliquemos ahora la fórmula de la regla de la cadena:
$$\frac{d}{dx} H(x) = \frac{d}{du}(f(u)) \cdot \frac{d}{dx}(g(x))$$
$$\frac{d}{dx} H(x) = \frac{d}{du}(\cos{(u)}) \cdot \frac{d}{dx}(12x^2+6x-3)$$
$$\frac{d}{dx} H(x) = (-\sin{(u)}) \cdot (24x+6)$$
Paso 4: Sustituye la función interna $latex g(x)=u$ en la ecuación derivada:
$$\frac{d}{dx} H(x) = (-\sin{(12x^2+6x-3)}) \cdot (24x+6)$$
Paso 5: Simplifica algebraicamente:
$$\frac{d}{dx} H(x) = -(24+6) \cdot \sin{(12x^2+6x-3)}$$
$$H'(x) = – (24 + 6) \sin{(12x^2+6x-3)}$$
EJEMPLO 4
¿Cuál es la derivada de la función dada?
$latex \csc{\ln{(12x+6)}}$
Solución
Paso 1: La fórmula de la regla de la cadena es:
$$ \frac{d}{dx} (H(x)) = \frac{d}{dx} \left(f(g(x)) \right) \cdot \frac{d}{x}(g(x))$$
Paso 2: Identifica cuántas funciones tienes en el problema. En este ejemplo, hay tres. Al separar estas tres funciones, tenemos
Si es que $latex g(h(x)) = u$, entonces
$latex f(g(h(x))) = f(u)$
$latex f(u) = \csc{(u)}$
Si es que $latex g(h(x)) = v$, entonces
$latex g(h(x)) = g(v)$
$latex g(v) = \ln{(v)}$
$latex v = h(x) = 12x+6$
Si es que $latex f(g(h(x))) = f(u)$, entonces
$$\frac{d}{dx} [f(g(h(x)))] = \frac{d}{du} [f(u)]$$
Si es que $latex g(h(x)) = g(v)$, entonces
$$\frac{d}{dx} [g(h(x))] = \frac{d}{dv} [g(v)]$$
Paso 3: Apliquemos ahora la fórmula de la regla de la cadena:
$$f_{1…n}'(x) = f_1′ \left( f_{2…n}(x) \right) \cdot f_2′ \left( f_{3…n}(x) \right)\cdots f_{n-1}’ \left(f_{n…n}(x)\right) \cdot f_n'(x)$$
$$\frac{d}{dx} H(x) = \frac{d}{du} f(u) \cdot \frac{d}{dv} g(v) \cdot \frac{d}{dx} h(x)$$
$$\frac{d}{dx} H(x) = \frac{d}{du}(\csc{(u)}) \cdot \frac{d}{dv}(\ln{(v)}) \cdot \frac{d}{dx}(12x+6)$$
$$\frac{d}{dx} H(x) = (-\csc{(u)} \cot{(u)}) \cdot (\frac{1}{v}) \cdot {12}$$
Paso 4: Substituye $latex g(h(x))$ y $latex h(x)$ en $latex u$ y $latex v$:
$$\frac{d}{dx} H(x) = (-\csc{(\ln{(12x+6)})} \cot{(\ln{(12x+6)})})\cdot (\frac{1}{12x+6}) \cdot {12}$$
Paso 5: Simplifica algebraicamente:
$$\frac{d}{dx} H(x) = \frac{-12 \csc{(\ln{(12x+6)})} \cot{(\ln{(12x+6)})}}{12x+6}$$
$$\frac{d}{dx} H(x) = \frac{-12 \csc{(\ln{(12x+6)})} \cot{(\ln{(12x+6)})}}{6(x+2)}$$
$$\frac{d}{dx} H(x) = \frac{-2 \csc{(\ln{(12x+6)})} \cot{(\ln{(12x+6)})}}{(x+2)}$$
$$H'(x) = -\frac{2 \csc{(\ln{(12x+6)})} \cot{(\ln{(12x+6)})}}{(x+2)}$$
EJEMPLO 5
Deriva lo siguiente:
$latex e^{\sin^{2}{(6x-3)}}$
Solución
Paso 1: Escribe la fórmula de la regla de la cadena como referencia:
$$\frac{d}{dx} (H(x)) = \frac{d}{dx} \left(f(g(x)) \right) \cdot \frac{d}{x}(g(x))$$
Paso 2: Identifica cuántas funciones tienes en el problema. En este ejemplo, hay cuatro. Al enumerar estas cuatro funciones, tenemos
Si es que $latex f(g(h(j(x)))) = u$, entonces
$latex f(g(h(j(x)))) = f(u)$
$latex f(u) = e^u$
Si es que $latex g(h(j(x))) = v$, entonces
$latex g(h(j(x))) = g(v)$
$latex g(v) = v^2$
Si es que $latex h(j(x)) = w$, entonces
$latex h(j(x)) = h(w)$
$latex h(w) = \sin{(w)}$
$latex w = j(x) = 6x-3$
Si es que $latex f(g(h(j(x)))) = f(u)$, entonces
$$\frac{d}{dx} [f(g(h(j(x))))] = \frac{d}{du} [f(u)]$$
Si es que $latex g(h(j(x))) = g(v)$, entonces
$$\frac{d}{dx} [g(h(j(x)))] = \frac{d}{dv} [g(v)]$$
Si es que $latex h(j(x)) = h(w)$, entonces
$$\frac{d}{dx} [h(j(x))] = \frac{d}{dw} [h(w)]$$
Paso 3: Apliquemos ahora la fórmula de la regla de la cadena:
$$f_{1…n}'(x) = f_1′ \left( f_{2…n}(x) \right) \cdot f_2′ \left( f_{3…n}(x) \right)\cdots f_{n-1}’ \left(f_{n…n}(x)\right) \cdot f_n'(x)$$
$$\frac{d}{dx} H(x) = \frac{d}{du} f(u) \cdot \frac{d}{dv} g(v) \cdot \frac{d}{dw} h(w) \cdot \frac{d}{dx} j(x)$$
$$\frac{d}{dx} H(x) = \frac{d}{du} (e^u) \cdot \frac{d}{dv} (v^2)\cdot \frac{d}{dw} (\sin{(w)}) \cdot \frac{d}{dx} (6x-3)$$
$$\frac{d}{dx} H(x) = (e^u) \cdot (2v) \cdot (\cos{(w)}) \cdot (6)$$
Paso 4: Substituye $latex g(h(j(x)))$, $latex h(j(x))$, y $latex j(x)$ en $latex u$, $latex v$, y $latex w$:
$$\frac{d}{dx} H(x) = (e^{\sin^{2}{(6x-3)}}) \cdot (2(\sin{(6x-3)}))\cdot (\cos{(6x-3)}) \cdot (6)$$
Paso 5: Simplifica algebraicamente:
$$\frac{d}{dx} H(x) = 12 \cdot \sin{(6x-3)} \cdot \cos{(6x-3)} \cdot e^{\sin^{2}{(6x-3)}}$$
$$H'(x) = 12 \sin{(6x-3)} \cos{(6x-3)} e^{\sin^{2}{(6x-3)}}$$
Regla de la cadena de derivadas – Problemas de práctica
Obtén la derivada de $latex f(x) = \ln{(e^x)}$
Escribe la respuesta en la casilla.
Veáse también
¿Interesado en aprender más sobre la regla de la cadena? Echa un vistazo a estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
