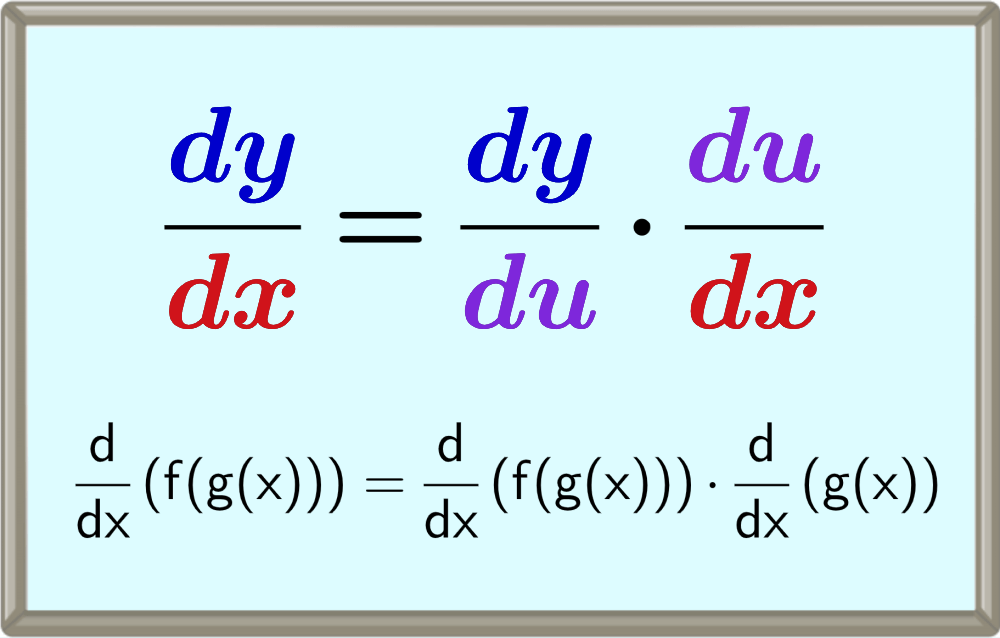La regla de la cadena es una de las principales herramientas utilizadas en aplicaciones de Cálculo Diferencial (o Cálculo I). Es muy esencial para la derivación de composiciones de al menos dos tipos diferentes de funciones.
Sin embargo, tan fácil como parece usar una fórmula estándar para derivar la composición de funciones, es importante aprender los conceptos y fundamentos detrás de esta fórmula estándar. Por lo tanto, en este artículo nos concentraremos principalmente en las demostraciones de la fórmula de la regla de la cadena.
¿Qué es la regla de la cadena?
La regla de la cadena se define como la derivada de la composición de al menos dos tipos diferentes de funciones. Esta regla se puede usar para derivar una composición de funciones como:
$$y’ = \frac{d}{dx}[f \left( g(x) \right)]$$
donde g(x) es un dominio de la función f. En esta composición, las funciones f y g deben ser dos tipos diferentes de funciones, que no pueden evaluarse algebraicamente en un solo tipo de función.
Pero, ¿cómo derivamos exactamente esa función dada usando la regla de la cadena?
La regla de la cadena establece que la derivada de una composición de al menos dos tipos diferentes de funciones es igual a la derivada de la función exterior f, multiplicada por la derivada de su función interior g. La función g será el dominio de la derivada de la función exterior f.
Para ilustrarlo mejor, tenemos
$$\frac{d}{dx} (f(g(x))) = \frac{d}{dx} (f(g(x))) \cdot \frac{d}{x}(g(x))$$
donde derivamos la función externa f usando el método de derivada de la función f mientras componemos la forma original de la función g como su dominio y luego multiplicamos la cantidad total por la derivada de la función interna g o g(x).
También podemos ilustrar la fórmula de la regla de la cadena como:
$$\frac{dy}{dx} = \frac{dy}{du}\cdot \frac{du}{dx}$$
en donde
- $latex f(u) =$ la función exterior
- $latex u = g(x)$, el dominio de la función externa $latex f(u)$
- $latex \frac{dy}{du} =$ la derivada de la función externa $latex f(u)$ en términos de $latex u$
- $latex \frac{du}{dx} $ la derivada de la función interna $latex g(x)$ en términos de $latex x$
La mayoría de las veces, esta forma de fórmula se usa para principiantes. Aunque tiene más pasos, se ha demostrado que es más conveniente y menos confuso. Esta forma usa un método de sustitución en la fórmula de la regla de la cadena para derivar las funciones externas.
Algo fácil, ¿verdad? Pero no debemos tomar esta fórmula superficialmente si pretendemos poder derivar cualquier composición de funciones. Para aprender y comprender los conceptos detrás del desarrollo de esta fórmula de la regla de la cadena, debemos estar familiarizados con cualquier demostración que satisfaga el enunciado de la regla de la cadena.
Demostración de la regla de la cadena
Para comprender esta demostración, se recomienda estar familiarizado con los temas la pendiente de una recta tangente y Derivadas usando límites.
Podemos recordar que una derivada puede expresarse en términos de límites de la siguiente manera:
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{f(x+h)-f(x)}{h}}$$
Ahora, supongamos que tenemos la siguiente función:
$latex H(x) = f(g(x))$
Entonces, si obtenemos la derivada, tenemos,
$$H'(x) = \frac{d}{dx} \left( f(g(x)) \right)$$
Podemos usar la derivación en términos de límites:
$$H'(x) = \lim \limits_{h \to 0} {\frac{H(x+h)-H(x)}{h}}$$
Sustituyendo la ecuación $latex H(x) = f(g(x))$, tenemos
$$H'(x) = \lim \limits_{h \to 0} {\frac{f(g(x+h)) – f(g(x))}{h}}$$
¿Qué manipulaciones podemos hacer en este límite para llegar a la fórmula de la regla de la cadena?
En nuestro límite, podemos multiplicar la función por
$$\frac{g(x+h)-g(x)}{g(x+h)-g(x)}$$
que es básicamente igual a uno. Por lo tanto, no cambiará nuestro límite en absoluto. Al hacerlo, tenemos
$$\frac{d}{dx} \left( f(g(x)) \right) = \lim \limits_{h \to 0} \left( {\frac{f(g(x+h)) – f(g(x))}{h}} \cdot \frac{g(x+h)-g(x)}{g(x+h)-g(x)} \right)$$
Como tenemos un producto de dos fracciones en nuestra ecuación, podemos aplicar la propiedad conmutativa de la multiplicación en sus denominadores. Al hacerlo, tenemos
$$\frac{d}{dx} \left( f(g(x)) \right) = \lim \limits_{h \to 0} \left( {\frac{f(g(x+h)) – f(g(x))}{g(x+h)-g(x)}} \cdot \frac{g(x+h)-g(x)}{h} \right)$$
Aplicando las propiedades de los límites, tenemos
$$\frac{d}{dx} \left( f(g(x)) \right) = \lim \limits_{h \to 0} \left(\frac{f(g(x+h)) – f(g(x))}{g(x+h)-g(x)} \right) \cdot \lim \limits_{h \to 0} \left(\frac{g(x+h)-g(x)}{h} \right)$$
La segunda parte del lado derecho es simplemente la derivada de g(x) escrita en limites. Entonces tenemos
$$\frac{d}{dx} \left( f(g(x)) \right) = \lim \limits_{h \to 0} \left(\frac{f(g(x+h)) – f(g(x))}{g(x+h)-g(x)} \right) \cdot \frac{d}{dx}(g(x))$$
Podemos usar las leyes de los límites para reorganizar nuestro límite de esta manera:
$$ \frac{d}{dx} \left( f(g(x)) \right) = \lim \limits_{h \to 0} \left(\frac{1}{g(x+h)-g(x)} \right) \cdot \lim \limits_{h \to 0} \Big( f(g(x+h)) – f(g(x)) \Big) \cdot \frac{d}{dx}(g(x))$$
Marcamos esta ecuación como $latex EQ.01$
Pero antes de evaluar $latex EQ.01$, usemos
$latex \gamma = g(x+h)-g(x)$
Marcamos esta ecuación como $latex EQ.02$
Igualando $latex EQ.02$ en términos de $latex g(x+h)$, tenemos
$latex g(x+h) = g(x) + \gamma$
Marcamos esta ecuación como $latex EQ.03$
Si evaluamos
$$\lim \limits_{h \to 0} \left( \frac{1}{g(x+h)-g(x)} \right)$$
Marquemos esta expresión como $latex ex.01$
de $latex EQ.01$, tenemos
$$\lim \limits_{h \to 0} \left( \frac{1}{g(x+h)-g(x)} \right) = \lim \limits_{h \to 0} \left( \frac{1}{\gamma} \right) $$
$$\lim \limits_{h \to 0} \left( \lim \limits_{h \to 0} \left( \frac{1}{\gamma} \right)\right) = \lim \limits_{h \to 0} \left( \lim \limits_{h \to 0} \left( \frac{1}{0} \right)\right) $$
Y si evaluamos el límite de $latex ex.01$ en términos de $latex \gamma \to 0$, tenemos
$$\lim \limits_{\gamma \to 0} \left( \lim \limits_{h \to 0} \left( \frac{1}{\gamma} \right) \right)= \lim \limits_{\gamma \to 0} \left( \lim \limits_{h \to 0} \left( \frac{1}{0} \right) \right)$$
Debido a esto, podemos concluir que
$latex h \to 0 = \gamma \to 0$
Por lo tanto, ahora podemos evaluar $latex EQ.01$ en términos de $latex \gamma \to 0$ en lugar de $latex h \to 0$ para resolver nuestros límites restantes. Así, tenemos
$$\frac{d}{dx} \left( f(g(x)) \right) = \lim \limits_{\gamma \to 0} \left( \frac{1}{g(x+h)-g(x)} \right) \cdot \lim \limits_{\gamma \to 0} \Big( f(g(x+h))– f(g(x)) \Big) \cdot \frac{d}{dx}(g(x))$$
Marcamos esta ecuación como $latex EQ.04$
Sustituyendo $latex EQ.02$ y $latex EQ.03$ en $latex EQ.04$, tenemos
$$\frac{d}{dx} \left( f(g(x)) \right) = \lim \limits_{\gamma \to 0} \left( \frac{1}{\gamma} \right) \cdot \lim \limits_{\gamma \to 0} \Big( f(g(x) + \gamma) – f(g(x)) \Big) \cdot \frac{d}{dx}(g(x))$$
Multiplicando la ecuación anterior, tenemos
$$\frac{d}{dx} \left( f(g(x)) \right) = \lim \limits_{\gamma \to 0} \left( {\frac{f(g(x) + \gamma) – f(g(x))}{\gamma}} \right) \cdot \frac{d}{dx}(g(x))$$
Resolviendo el límite restante, tenemos
$$\frac{d}{dx} \left( f(g(x)) \right) = \frac{d}{dx} \left( f(g(x)) \right) \cdot \frac{d}{dx}(g(x))$$
o puede ser simplemente ilustrado como
$$H'(x) = \left( f(g(x)) \right)’ \cdot g'(x)$$
que ahora es la fórmula de la regla de la cadena.
Finalmente, hemos demostrado la fórmula de la regla de la cadena mediante la aplicación de los conceptos de límites.
Veáse también
¿Interesado en aprender más sobre la regla de la cadena? Echa un vistazo a estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
