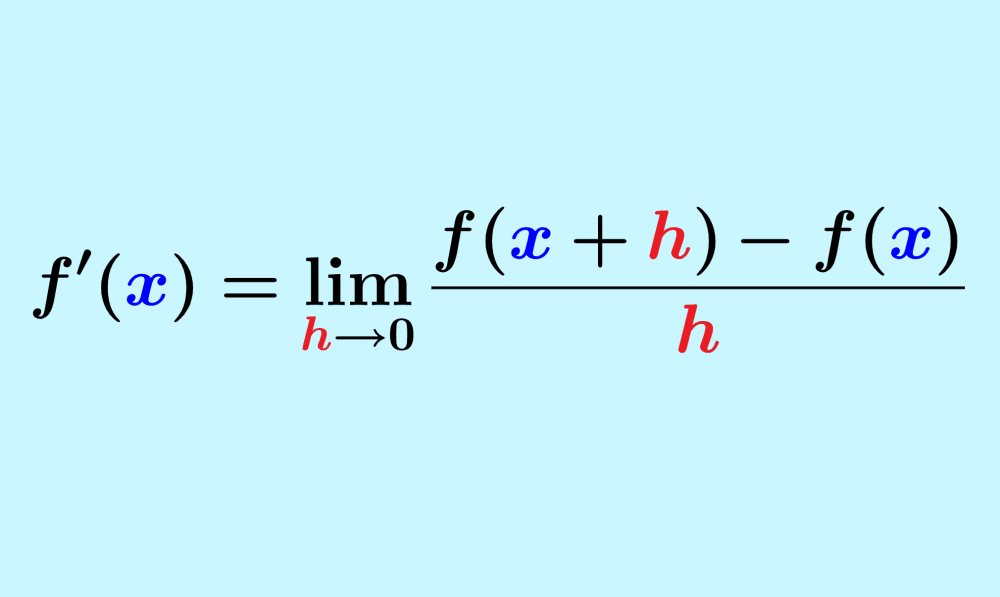La definición de la derivada como un límite puede ser encontrada al usar la fórmula de la pendiente para encontrar la pendiente de la recta secante entre dos puntos de la función. Luego, usamos un límite para acercar a los puntos, de modo que la pendiente de la secante sea una aproximación a la pendiente de la tangente.
A continuación, aprenderemos sobre la definición de la derivada como un límite. Usaremos un diagrama para encontrar esta definición paso a paso. Luego, aplicaremos esta idea para calcular algunas derivadas.
Cómo definir a la derivada usando límites
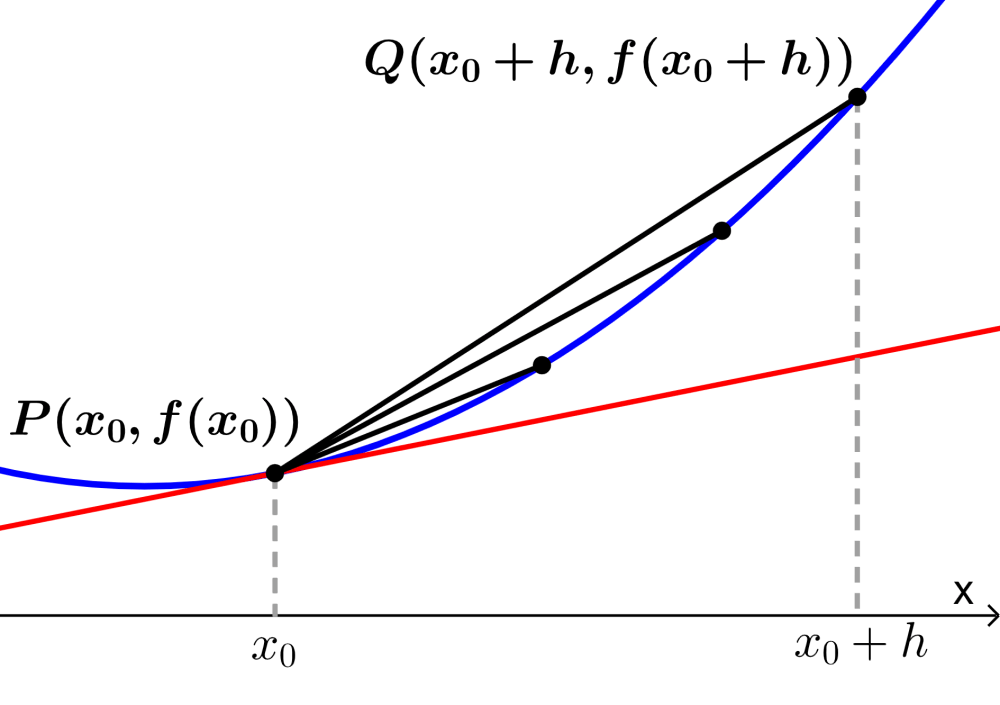
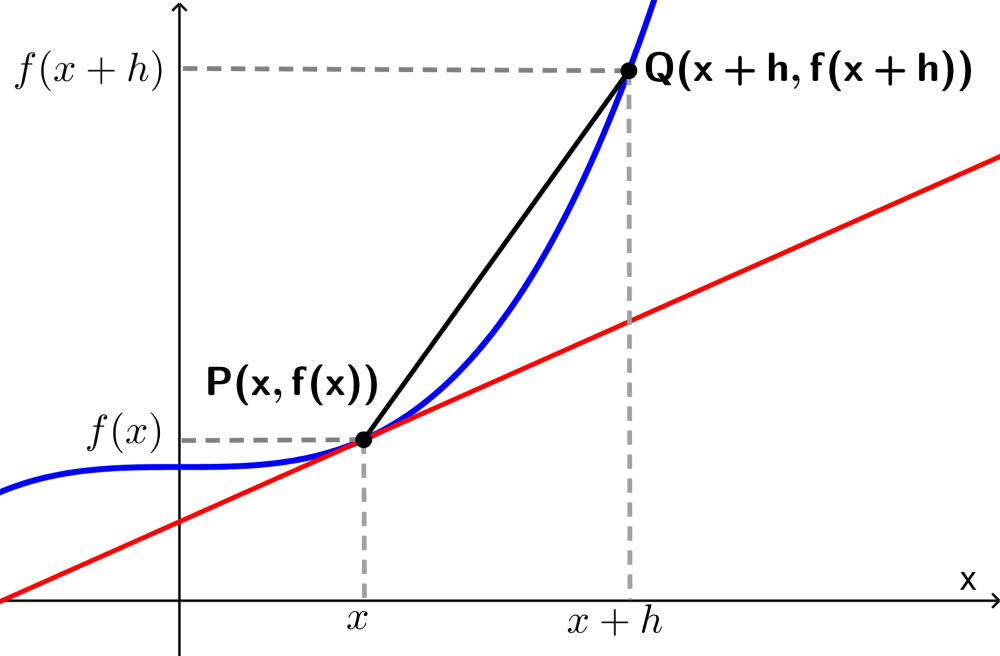
Vamos a usar límites para encontrar una ecuación que nos permita calcular la pendiente de la recta tangente a una función. Para esto usamos el siguiente diagrama:
Consideremos al punto $latex P~(x_{0},~ f(x_{0}))$ que se encuentra en la curva producida por la función $latex f(x)$, como se muestra en el diagrama. Vamos a encontrar la pendiente de la recta tangente a f en el punto P.
Podemos encontrar la pendiente usando el punto $latex Q~(x_{0}+h,~f(x_{0}+h)$, el cual se encuentra a h unidades de P y asumimos que h es muy pequeño.
Entonces, empezamos calculando la pendiente de la recta secante PQ. Sabemos que la pendiente es igual al cambio en y sobre el cambio en x. Entonces, tenemos:
$$\text{Pendiente de PQ}=\frac{f(x_{0}+h)-f(x_{0})}{x_{0}+h-x_{0}}$$
$$\text{Pendiente de PQ}=\frac{f(x_{0}+h)-f(x_{0})}{h}$$
Si es que h es lo suficientemente pequeño, el punto Q se acercará cada vez más a P hasta que la pendiente de la recta secante PQ será una buena aproximación para la pendiente de la recta tangente en P.
Entonces, definimos a la pendiente de la recta tangente como el límite de la pendiente de la recta secante a medida que h se acerca a 0:
$$m_{tan}=\lim _{h \to 0}\frac{f(x_{0}+h)-f(x_{0})}{h}$$
Ahora, en vez de usar la constante $latex x_{0}$, podemos usar la variable $latex x$. De este modo, el límite resultante será una expresión en términos de x.
Esta expresión puede ser considerada como una función de x. Además, esta función, la cual puede ser denotada por $latex f'(x)$, es la derivada de la función f.
Entonces, si es que tenemos que $latex f(x)$ es una función de x, la derivada de f en x es:
$$f'(x)=\lim _{h \to 0}\frac{f(x+h)-f(x)}{h}$$
Derivadas como razón de cambio
La derivada de una función $latex f(x)$ en x es la razón instantánea de cambio de la función en x. Esto se debe a que la derivada es definida como el límite, el cual encuentra la pendiente de la recta tangente a una función.
Recordemos que la pendiente representa el cambio en y sobre el cambio en x. Es decir, tenemos una razón de cambio con respecto a x.
Si es que $latex y=f(x)$ es una función de x, entonces, también podemos usar la notación $latex \frac{dy}{dx}$ para representar a la derivada de f.
$latex \frac{dy}{dx}$ es la derivada de y con respecto a x. Es decir, esto es la razón a la cual y cambia cuando x cambia.
Por ejemplo, si es que $latex d(t)$ representa al desplazamiento de un auto en un tiempo t, entonces, $latex d'(t)$ representa la velocidad el auto en un tiempo t. Si es que $latex y=f(x)$ es una función de x, entonces, $latex f'(x)$ representa cómo y cambia cuando x cambia.
Si es que $latex f'(x)$ es positivo en un cierto punto, entonces, y incrementa a medida que x incrementa. Si es que $latex f'(x)$ es negativo en un cierto punto, entonces, y decrece a medida que x incrementa.
Ejemplos de derivadas usando límites
Los siguientes son algunos ejemplos de cómo encontrar la derivada de una función usando la su definición como límites.
EJEMPLO 1
Encuentra la derivada de $latex f(x)=10x$ usando la definición de derivada por límites.
Solución: Una derivada puede ser encontrada usando la siguiente fórmula:
$$f'(x)=\lim _{h \to 0}\frac{f(x+h)-f(x)}{h}$$
Entonces, usamos la función $latex f(x)=10x$ en el numerador y tenemos:
$$f'(x)=\lim _{h \to 0}\frac{10(x+h)-10x}{h}$$
$$f'(x)=\lim _{h \to 0}\frac{10x+10h-10x}{h}$$
$$f'(x)=\lim _{h \to 0}\frac{10h}{h}$$
Simplificando la h del numerador con la h del denominador, tenemos:
$$f'(x)=\lim _{h \to 0}(10)$$
Dado que no tenemos ninguna h, simplemente removemos el límite:
$latex f'(x)=10$
EJEMPLO 2
Encuentra la derivada de $latex f(x)=3x^2$ usando la definición de la derivada con límites.
Solución: Usamos la fórmula:
$$f'(x)=\lim _{h \to 0}\frac{f(x+h)-f(x)}{h}$$
Entonces, reescribimos al numerador usando $latex f(x)=3x^2$ y tenemos:
$$f'(x)=\lim _{h \to 0}\frac{3(x+h)^2-3x^2}{h}$$
$$f'(x)=\lim _{h \to 0}\frac{3x^2+6hx+3h^2-3x^2}{h}$$
$$f'(x)=\lim _{h \to 0}\frac{6hx+3h^2}{h}$$
Podemos factorizar la h del numerador y simplificar con el denominador:
$$f'(x)=\lim _{h \to 0}\frac{h(6x+3h)}{h}$$
$$f'(x)=\lim _{h \to 0}(6x+3h)$$
Finalmente, resolvemos el límite al sustituir $latex h=0$ en la expresión:
$latex f'(x)=6x+3(0)$
$latex f'(x)=6x$
EJEMPLO 3
Encuentra la derivada de $latex f(x)=5x^2+6x$ usando límites.
Solución: La fórmula de la derivada de una función usando límites es:
$$f'(x)=\lim _{h \to 0}\frac{f(x+h)-f(x)}{h}$$
Entonces, usando la función $latex f(x)=5x^2+6x$ en el numerador, tenemos:
$$f'(x)=\lim _{h \to 0}\frac{(5(x+h)^2+6(x+h))-(5x^2+6x)}{h}$$
$$f'(x)=\lim _{h \to 0}\frac{5(x^2+2hx+h^2)+6x+6h-5x^2-6x}{h}$$
$$f'(x)=\lim _{h \to 0}\frac{5x^2+10hx+5h^2+6x+6h-5x^2-6x}{h}$$
$$f'(x)=\lim _{h \to 0}\frac{10hx+5h^2+6h}{h}$$
Factorizamos la h del numerador para simplificar con la h del denominador:
$$f'(x)=\lim _{h \to 0}\frac{h(10x+5h+6)}{h}$$
$$f'(x)=\lim _{h \to 0}(10x+5h+6)$$
Finalmente, resolvemos el límite al sustituir $latex h=0$ en la expresión:
$latex f'(x)=10x+5(0)+6$
$latex f'(x)=10x+6$
Véase también
¿Interesado en aprender más sobre derivadas de funciones? Puedes mirar estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
