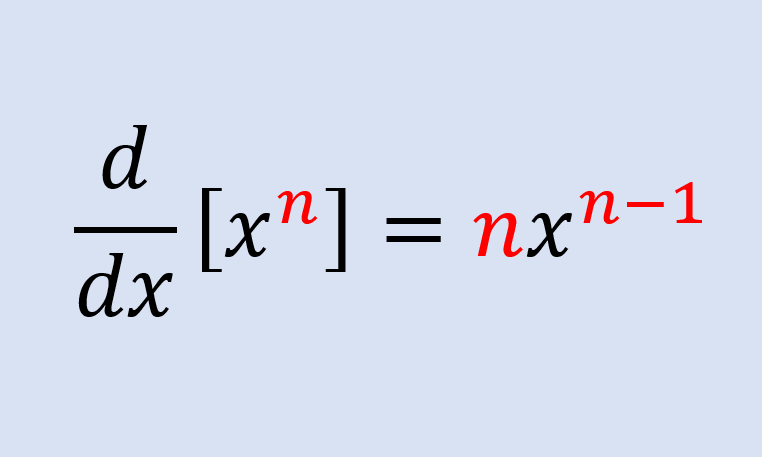La regla de la potencia es una de las fórmulas más utilizadas en Cálculo Diferencial. Esta regla es aplicada para resolver derivadas de funciones con un solo término. La regla de la potencia nos permite calcular derivadas fácilmente, ya que no tenemos que usar la fórmula de una derivada con límites.
A continuación, aprenderemos cómo encontrar derivadas de funciones con un solo término. Conoceremos la fórmula y la aplicaremos para resolver algunos ejercicios.
Definición y fórmula de la regla de la potencia
La regla de la potencia de derivadas nos dice que la derivada de una variable elevada a un exponente numérico es igual al valor del exponente numérico multiplicado por la variable elevada a la cantidad del exponente numérico restado por uno.
La regla de la potencia nos permite obtener derivadas de funciones con exponentes numéricos sin la necesidad de usar la fórmula de una derivada con límites.
También existen otras formas y casos de la regla de la potencia, como el caso de polinomios, pero serán revisados cuando aprendamos las reglas de derivadas aplicables.
Fórmula de la regla de la potencia básica
La fórmula de la regla de la potencia es:
| $$\frac{d}{dx}(x^n) = nx^{n-1}$$ |
donde
- $latex n =$ el valor numérico del exponente limitado solo a números reales
- $latex x =$ la variable que se eleva a un exponente numérico $latex n$
También podemos denotar a $latex \frac{d}{dx}(x^n)$ con $latex y’$, $latex F'(x)$, $latex f'(x)$, u otras letras usadas para denotar funciones con el símbolo del apóstrofe.
Pasos para usar la regla de la potencia
Supongamos que tenemos que derivar
$latex f(x) = x^2$
Tenemos una función con una variable elevada a una potencia de 2. Para derivar este problema vamos a usar la regla de la potencia como se muestra en los siguientes pasos:
Paso 1: Empezamos escribiendo la fórmula de la regla de potencia:
$latex f'(x^n) = nx^{n-1}$
Paso 2: Si la función contiene o radicales o expresiones racionales, usamos las leyes de los exponentes para convertir a la forma exponencial. En este caso, no tenemos radicales o expresiones racionales.
Nota: Un ejemplo sería escribir a $latex \sqrt{x}$ como $latex x^{\frac{1}{2}}$.
Paso 3: Determina el exponente de la variable. En este caso, nuestro exponente es 2. Por lo tanto,
$latex n = 2$
Paso 4: Aplica la fórmula de la regla de la potencia para derivar el problema:
$$\frac{d}{dx} (x^n) = \frac{d}{dx} (x^2)$$
$$\frac{d}{dx} (x^2) = 2 \cdot x^{2-1}$$
Paso 5: Simplifica la expresión resultante:
$$\frac{d}{dx} (x^2) = 2x^{1}$$
$$f'(x) = 2x$$
Puedes usar $latex f'(x), y’,$ o $latex \frac{d}{dx}(f(x))$ como símbolo de derivada en el lado izquierdo de la respuesta final en lugar de $latex (x^n)’$ o $latex \frac{d}{dx}(x^n)$.
Ejemplos de la regla de la potencia de derivadas
Cada uno de los siguientes ejemplos tiene su respectiva solución detallada, en donde aplicamos la regla de la potencia.
EJEMPLO 1
Encuentra la derivada de $latex f(x)=x^3$.
Solución
Paso 1: Empezamos con la fórmula:
$latex f'(x^n) = nx^{n-1}$
Paso 2: La expresión tiene un exponente numérico, por lo que no tenemos que realizar este paso.
Paso 3: En este caso, el exponente es 3. Entonces,
$latex n = 3$
Paso 4: Usando la regla de la potencia, tenemos:
$$\frac{d}{dx} (x^n) = \frac{d}{dx} (x^3)$$
$$\frac{d}{dx} (x^3) = 3 \cdot x^{3-1}$$
Paso 5: Simplificando, tenemos:
$$\frac{d}{dx} (x^3) = 3 x^2$$
$$f'(x)= 3 x^2$$
EJEMPLO 2
Encuentra la derivada de la función $latex f(x)=5x^4$.
Solución
Paso 1: Tenemos la fórmula:
$latex f'(x^n) = nx^{n-1}$
Paso 2: El exponente de la variable es un número entero, por lo que no tenemos que reescribirlo.
Paso 3: En este caso, el exponente es 4. Entonces,
$latex n = 4$
Paso 4: Al aplicar la regla de la potencia, tenemos:
$$\frac{d}{dx} (x^n) = \frac{d}{dx} (5x^4)$$
$$\frac{d}{dx} (5x^4) = 4 \cdot (5x^{4-1})$$
Paso 5: Simplificando, tenemos:
$$\frac{d}{dx} (5x^4) = 20 x^3$$
$$f'(x)= 20 x^3$$
EJEMPLO 3
Determina la derivada de la función $latex f(x)=10x^7$.
Solución
Paso 1: La fórmula de la regla de la potencia de derivadas es:
$latex f'(x^n) = nx^{n-1}$
Paso 2: La expresión tiene un exponente numérico, por lo que no tenemos que realizar este paso.
Paso 3: El exponente de la expresión es 7. Entonces, tenemos:
$latex n = 7$
Paso 4: Cuando aplicamos la regla de la potencia, tenemos:
$$\frac{d}{dx} (x^n) = \frac{d}{dx} (10x^7)$$
$$\frac{d}{dx} (10x^7) = 7 \cdot (10x^{7-1})$$
Paso 5: Simplificando, tenemos:
$$\frac{d}{dx} (10x^7) = 70 x^6$$
$$f'(x)= 70 x^6$$
EJEMPLO 4
Deriva la función: $latex f(x) = -12x^{-13}$.
Solución
Paso 1: Tenemos la fórmula:
$latex f'(x^n) = nx^{n-1}$
Paso 2: La expresión está dada en forma exponencial, por lo que podemos saltarnos este paso.
Paso 3: Determina el exponente de la variable. En este caso, nuestro exponente es -13. Entonces,
$latex n = -13$
Paso 4: Derivamos usando la regla de la potencia:
$$\frac{d}{dx} (x^n) = \frac{d}{dx} (-12x^{-13})$$
$$\frac{d}{dx} (-12x^{-13}) = -13 \cdot (-12 x^{-13-1})$$
Paso 5: Simplificando, tenemos:
$$\frac{d}{dx} (-12x^{-13}) = 156x^{-14}$$
Dado que el exponente es negativo, podemos aplicar las leyes de los exponentes para simplificarlo aún más en forma racional, aunque esto es opcional:
$$\frac{d}{dx} (x^n) = \frac{156}{x^{14}}$$
La respuesta final es:
$$f'(x) = \frac{156}{x^{14}}$$
EJEMPLO 5
Encuentra la derivada de $latex f(x)=\sqrt{x}$.
Solución
Paso 1: Empezamos con la fórmula de la regla de la potencia:
$latex f'(x^n) = nx^{n-1}$
Paso 2: Tenemos que usar la ley de exponentes radicales para reescribir a la expresión:
$$ \sqrt{x}=x^{\frac{1}{2}}$$
Paso 3: Ahora, vemos que el exponente es 1/2. Entonces,
$latex n = \frac{1}{2}$
Paso 4: Usando la regla de la potencia en la función, tenemos:
$$\frac{d}{dx} (x^n) = \frac{d}{dx} (x^{\frac{1}{2}})$$
$$\frac{d}{dx} (x^{\frac{1}{2}}) = \frac{1}{2} \cdot ( x^{\frac{1}{2}-1})$$
Paso 5: Simplificando, tenemos:
$$f'(x) = \frac{1}{2} x^{-\frac{1}{2}}$$
Podemos usar las leyes de los exponentes, para escribir de la siguiente forma:
$$f'(x) = \frac{1}{2x^{\frac{1}{2}}}$$
$$f'(x) = \frac{1}{2\sqrt{x}}$$
EJEMPLO 6
Encuentra la derivada de $latex f(x)=\frac{1}{\sqrt{x}}$.
Solución
Paso 1: La fórmula de la regla de la potencia es:
$latex f'(x^n) = nx^{n-1}$
Paso 2: Usando las reglas de los exponentes, podemos escribir de la siguiente forma:
$$ \frac{1}{\sqrt{x}}=x^{-\frac{1}{2}}$$
Paso 3: El exponente de la expresión es -1/2. Entonces, tenemos:
$latex n = -\frac{1}{2}$
Paso 4: Al aplicar la regla de la potencia en la función, tenemos:
$$\frac{d}{dx} (x^n) = \frac{d}{dx} (x^{-\frac{1}{2}})$$
$$\frac{d}{dx} (x^{-\frac{1}{2}}) = -\frac{1}{2} \cdot ( x^{-\frac{1}{2}-1})$$
Paso 5: Simplificando, tenemos:
$$f'(x) = -\frac{1}{2} x^{-\frac{3}{2}}$$
Usamos las leyes de los exponentes para escribir de la siguiente forma:
$$f'(x) = -\frac{1}{2x^{\frac{3}{2}}}$$
$$f'(x) = -\frac{1}{2\sqrt{x^3}}$$
Regla de la potencia de derivadas – Ejercicios para resolver
Usa la regla de la potencia para encontrar las derivadas de las siguientes funciones.
Véase también
¿Interesado en aprender más sobre derivadas de funciones? Puedes mirar estas páginas: