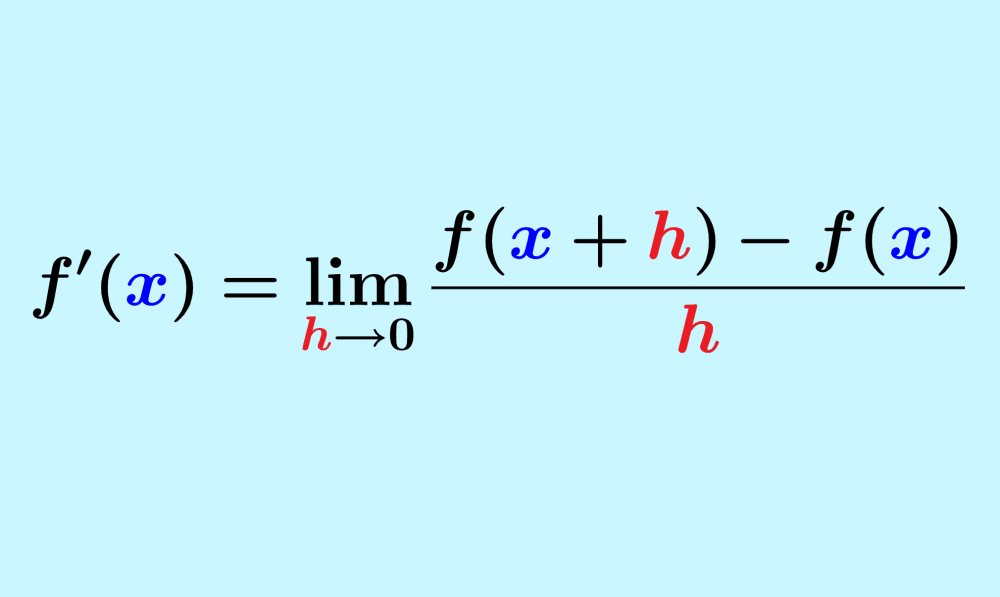Las derivadas pueden ser calculadas usando la definición de una derivada con límites. Esta definición consiste en usar el límite para encontrar la pendiente de una recta secante a dos puntos en la función, de modo que se aproxime al valor de la pendiente de la recta tangente.
A continuación, veremos 10 ejercicios resueltos de derivadas usando límites. Además, podrás poner a prueba tus habilidades con algunos ejercicios de práctica.
Cómo resolver derivadas usando límites
Para calcular la derivada de una función usando límites, podemos usar la siguiente fórmula:
$$f'(x)=\lim _{h \to 0}\frac{f(x+h)-f(x)}{h}$$
Esta fórmula tiene las siguientes partes importantes:
- $latex f(x+h)$. Esto significa que tenemos que evaluar a la función dada usando la entrada $latex x+h$.
- $latex f(x)$. Esta es la función original en términos de x.
- h en el denominador. Este valor debe permanecer igual hasta que evaluemos el límite o hasta que sea simplificado.
- $latex \lim _{h \to 0}$ es el límite. Generalmente, lo resolvemos al sustituir por 0 a todas las h que encontremos.
Entonces, para aplicar esta fórmula, tenemos que empezar encontrando la expresión $latex f(x+h)$ en el numerador. Luego, sustraímos la función original $latex f(x)$.
Generalmente, podremos simplificar la h del denominador con la h del numerador. Por último, usamos $latex h=0$ para resolver el límite (esto funcionará en la mayoría de casos, pero no en todos).
10 Ejercicios de derivadas usando límites resueltos
EJERCICIO 1
Encuentra la derivada de $latex f(x)=8x$ usando límites.
Solución
Para encontrar la derivada de una función con límites, tenemos que usar la siguiente fórmula:
$$f'(x)=\lim _{h \to 0}\frac{f(x+h)-f(x)}{h}$$
Entonces, usamos la función $latex f(x)=8x$ para reescribir al numerador y tenemos:
$$f'(x)=\lim _{h \to 0}\frac{8(x+h)-8x}{h}$$
$$f'(x)=\lim _{h \to 0}\frac{8x+8h-8x}{h}$$
$$f'(x)=\lim _{h \to 0}\frac{8h}{h}$$
Ahora, podemos simplificar la h del numerador con la h del denominador:
$$f'(x)=\lim _{h \to 0}(8)$$
Como ya no tenemos ninguna h, simplemente removemos el límite:
$latex f'(x)=8$
EJERCICIO 2
Usa límites para encontrar la derivada de $latex f(x)=x^2$.
Solución
Usamos la siguiente fórmula para encontrar la derivada:
$$f'(x)=\lim _{h \to 0}\frac{f(x+h)-f(x)}{h}$$
Ahora, usamos $latex f(x)=x^2$ en el numerador y tenemos:
$$f'(x)=\lim _{h \to 0}\frac{(x+h)^2-x^2}{h}$$
$$f'(x)=\lim _{h \to 0}\frac{x^2+2hx+h^2-x^2}{h}$$
$$f'(x)=\lim _{h \to 0}\frac{2hx+h^2}{h}$$
Factorizando la h del numerador y simplificando con la h del denominador, tenemos:
$$f'(x)=\lim _{h \to 0}\frac{h(2x+h)}{h}$$
$$f'(x)=\lim _{h \to 0}(2x+h)$$
Podemos resolver el límite al sustituir $latex h=0$ en la expresión:
$latex f'(x)=2x+0$
$latex f'(x)=2x$
EJERCICIO 3
Calcula la derivada de $latex f(x)=4x^2+5$ usando límites.
Solución
Usamos la fórmula de una derivada por límites:
$$f'(x)=\lim _{h \to 0}\frac{f(x+h)-f(x)}{h}$$
Para resolver, usamos la función $latex f(x)=4x^2+5$ en el numerador de la fórmula:
$$f'(x)=\lim _{h \to 0}\frac{(4(x+h)^2+5)-(4x^2+5)}{h}$$
$$f'(x)=\lim _{h \to 0}\frac{4(x^2+2hx+h^2)+5-4x^2-5}{h}$$
$$f'(x)=\lim _{h \to 0}\frac{4x^2+8hx+4h^2+5-4x^2-5}{h}$$
$$f'(x)=\lim _{h \to 0}\frac{8hx+4h^2}{h}$$
Podemos factorizar la h del numerador y simplificar con la h del denominador:
$$f'(x)=\lim _{h \to 0}\frac{h(8x+4h)}{h}$$
$$f'(x)=\lim _{h \to 0}(8x+4h)$$
Para resolver el límite, sustituimos $latex h=0$ en la expresión:
$latex f'(x)=8x+4(0)$
$latex f'(x)=8x$
EJERCICIO 4
Determina la derivada de $latex f(x)=3x^2+5x$ usando límites.
Solución
Empezamos con la siguiente fórmula:
$$f'(x)=\lim _{h \to 0}\frac{f(x+h)-f(x)}{h}$$
Ahora, usamos la función $latex f(x)=3x^2+5x$ en el numerador y tenemos:
$$f'(x)=\lim _{h \to 0}\frac{(3(x+h)^2+5(x+h))-(3x^2+5x)}{h}$$
$$f'(x)=\lim _{h \to 0}\frac{3(x^2+2hx+h^2)+5x+5h-3x^2-5x}{h}$$
$$f'(x)=\lim _{h \to 0}\frac{3x^2+6hx+3h^2+5x+5h-3x^2-5x}{h}$$
$$f'(x)=\lim _{h \to 0}\frac{6hx+3h^2+5h}{h}$$
Al factorizar la h del numerador y simplificando con el denominador, tenemos:
$$f'(x)=\lim _{h \to 0}\frac{h(6x+3h+5)}{h}$$
$$f'(x)=\lim _{h \to 0}(6x+3h+5)$$
Para resolver el límite, usamos $latex h=0$ y tenemos:
$latex f'(x)=6x+3(0)+5$
$latex f'(x)=6x+5$
EJERCICIO 5
Encuentra la derivada de $latex f(x)=4x^2-7x$ usando límites.
Solución
Tenemos la siguiente fórmula:
$$f'(x)=\lim _{h \to 0}\frac{f(x+h)-f(x)}{h}$$
Entonces, usamos a la función $latex f(x)=4x^2-7x$ en el numerador para reescribirlo:
$$f'(x)=\lim _{h \to 0}\frac{(4(x+h)^2-7(x+h))-(4x^2-7x)}{h}$$
$$f'(x)=\lim _{h \to 0}\frac{4(x^2+2hx+h^2)-7x-7h-4x^2+7x}{h}$$
$$f'(x)=\lim _{h \to 0}\frac{4x^2+8hx+4h^2-7x-7h-4x^2+7x}{h}$$
$$f'(x)=\lim _{h \to 0}\frac{8hx+4h^2-7h}{h}$$
Podemos factorizar la h del numerador para simplificar con la h del denominador y tenemos:
$$f'(x)=\lim _{h \to 0}\frac{h(8x+4h-7)}{h}$$
$$f'(x)=\lim _{h \to 0}(8x+4h-7)$$
Finalmente, resolvemos el límite, usando $latex h=0$ y tenemos:
$latex f'(x)=8x+4(0)-7$
$latex f'(x)=8x-7$
EJERCICIO 6
Encuentra la derivada de la función $latex f(x)=6x-x^2$.
Solución
Empezamos con la fórmula de derivadas por límites:
$$f'(x)=\lim _{h \to 0}\frac{f(x+h)-f(x)}{h}$$
Ahora, usamos la función $latex f(x)=6x-x^2$ en el numerador y tenemos:
$$f'(x)=\lim _{h \to 0}\frac{(6(x+h)-(x+h)^2)-(6x-x^2)}{h}$$
$$f'(x)=\lim _{h \to 0}\frac{6x+6h-(x^2+2hx+h^2)-6x+x^2}{h}$$
$$f'(x)=\lim _{h \to 0}\frac{6x+6h-x^2-2hx-h^2-6x+x^2}{h}$$
$$f'(x)=\lim _{h \to 0}\frac{6h-2hx-h^2}{h}$$
Factorizamos la h del numerador para simplificar con la h del denominador:
$$f'(x)=\lim _{h \to 0}\frac{h(6-2x-h)}{h}$$
$$f'(x)=\lim _{h \to 0}(6-2x-h)$$
Usamos el valor $latex h=0$ en la expresión para resolver el límite:
$latex f'(x)=6-2x-0$
$latex f'(x)=6-2x$
EJERCICIO 7
Encuentra la derivada de $latex f(x)=x^3$ usando límites.
Solución
Empezamos con la siguiente fórmula:
$$f'(x)=\lim _{h \to 0}\frac{f(x+h)-f(x)}{h}$$
Usando la función $latex f(x)=x^3$ en el numerador, tenemos:
$$f'(x)=\lim _{h \to 0}\frac{(x+h)^3-x^3}{h}$$
$$f'(x)=\lim _{h \to 0}\frac{x^3+3x^2h+3xh^2+h^3-x^3}{h}$$
$$f'(x)=\lim _{h \to 0}\frac{3x^2h+3xh^2+h^3}{h}$$
Ahora, podemos factorizar la h del numerador para simplificar con el denominador:
$$f'(x)=\lim _{h \to 0}\frac{h(3x^2+3xh+h^2)}{h}$$
$$f'(x)=\lim _{h \to 0}(3x^2+3xh+h^2)$$
Usando la sustitución $latex h=0$, podemos resolver el límite:
$latex f'(x)=3x^2+3x(0)+0^2$
$latex f'(x)=3x^2$
EJERCICIO 8
Usa límites para encontrar la derivada de $latex f(x)=x^3+4x$
Solución
Tenemos la fórmula
$$f'(x)=\lim _{h \to 0}\frac{f(x+h)-f(x)}{h}$$
Entonces, usamos la función $latex f(x)=x^3+4x$ en el numerador y tenemos:
$$f'(x)=\lim _{h \to 0}\frac{((x+h)^3+4(x+h))-(x^3+4x)}{h}$$
$$f'(x)=\lim _{h \to 0}\frac{x^3+3x^2h+3xh^2+h^3+4x+4h-x^3-4x}{h}$$
$$f'(x)=\lim _{h \to 0}\frac{3x^2h+3xh^2+h^3+4h}{h}$$
Ahora, vamos a factorizar la h del numerador para simplificar:
$$f'(x)=\lim _{h \to 0}\frac{h(3x^2+3xh+h^2+4)}{h}$$
$$f'(x)=\lim _{h \to 0}(3x^2+3xh+h^2+4)$$
Para resolver el límite, usamos la sustitución $latex h=0$:
$latex f'(x)=3x^2+3x(0)+0^2+4$
$latex f'(x)=3x^2+4$
EJERCICIO 9
Usa límites para encontrar la derivada de $latex f(x)=\frac{1}{x}$.
Solución
Vamos a usar la fórmula:
$$f'(x)=\lim _{h \to 0}\frac{f(x+h)-f(x)}{h}$$
Entonces, usando la función $latex f(x)=\frac{1}{x}$ para reescribir el numerador, tenemos:
$$f'(x)=\lim _{h \to 0}\frac{\frac{1}{x+h}-\frac{1}{x}}{h}$$
Para simplificar al numerador, podemos usar el denominador común $latex (x+h)x$ para combinar y restar las fracciones:
$$f'(x)=\lim _{h \to 0}\frac{\frac{x-(x+h)}{x(x+h)}}{h}$$
$$f'(x)=\lim _{h \to 0}\frac{\frac{x-x-h}{x^2+xh)}}{h}$$
$$f'(x)=\lim _{h \to 0}\frac{\frac{-h}{x^2+xh)}}{h}$$
Ahora, reescribir a la fracción y simplificamos a la h del numerador y del denominador:
$$f'(x)=\lim _{h \to 0}\frac{-h}{h(x^2+xh)}$$
$$f'(x)=\lim _{h \to 0}\frac{-1}{x^2+xh}$$
Por último, vamos a resolver el límite sustituyendo $latex h=0$ en la expresión:
$$ f'(x)=\frac{-1}{x^2+x(0)}$$
$$f'(x)=-\frac{1}{x^2}$$
EJERCICIO 10
Usa límites para encontrar la derivada de la función raíz cuadrada, $latex f(x)=\sqrt{x}$.
Solución
Tenemos la fórmula:
$$f'(x)=\lim _{h \to 0}\frac{f(x+h)-f(x)}{h}$$
Usamos la función raíz cuadrada, $latex f(x)=\sqrt{x}$, para reescribir al numerador:
$$f'(x)=\lim _{h \to 0}\frac{\sqrt{x+h}-\sqrt{x}}{h}$$
La expresión del numerador puede ser simplificada al multiplicar tanto al numerador como al denominador por el conjugado del numerador:
$$f'(x)=\lim _{h \to 0}\frac{(\sqrt{x+h}-\sqrt{x})(\sqrt{x+h}+\sqrt{x})}{h(\sqrt{x+h}+\sqrt{x})}$$
$$f'(x)=\lim _{h \to 0}\frac{x+h-x}{h(\sqrt{x+h}+\sqrt{x})}$$
$$f'(x)=\lim _{h \to 0}\frac{h}{h(\sqrt{x+h}+\sqrt{x})}$$
Ahora, podemos simplificar la h del numerador con la h del denominador:
$$f'(x)=\lim _{h \to 0}\frac{1}{\sqrt{x+h}+\sqrt{x}}$$
Por último, podemos resolver el límite al sustituir $latex h=0$ en la expresión:
$$f'(x)=\lim _{h \to 0}\frac{1}{\sqrt{x+0}+\sqrt{x}}$$
$$f'(x)=\lim _{h \to 0}\frac{1}{\sqrt{x}+\sqrt{x}}$$
$$f'(x)=\lim _{h \to 0}\frac{1}{2\sqrt{x}}$$
Ejercicios de derivadas usando límites para resolver
Usa límites para encontrar la derivada de $latex f(x)=7x^2-8x$.
Escribe el resultado en la casilla.
Véase también
¿Interesado en aprender más sobre derivadas de funciones? Puedes mirar estas páginas: