La Regla del Cociente es una de las herramientas más útiles en Cálculo Diferencial (o Cálculo I) para derivar un cociente de dos funciones. Se puede usar junto con cualquier tipo de función existente siempre que las operaciones de división estén presentes en el problema de derivación dado.
Aquí, nos centraremos principalmente en las demostraciones de la fórmula de la regla del cociente aplicando los conceptos de derivación mediante límites y la regla de la cadena. Además, veremos algunos ejemplos de derivación de funciones que usan la fórmula de la regla del cociente.
CÁLCULO
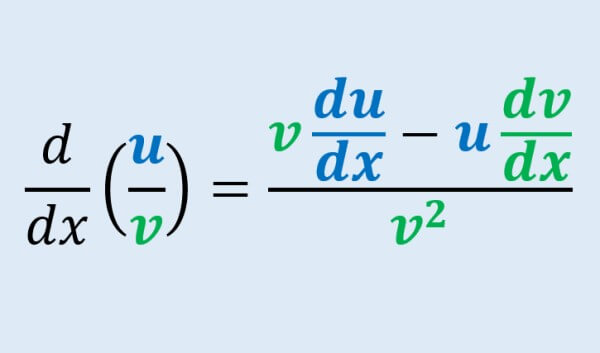
Relevante para…
Aprender sobre las diferentes demostraciones de la regla del cociente.
CÁLCULO
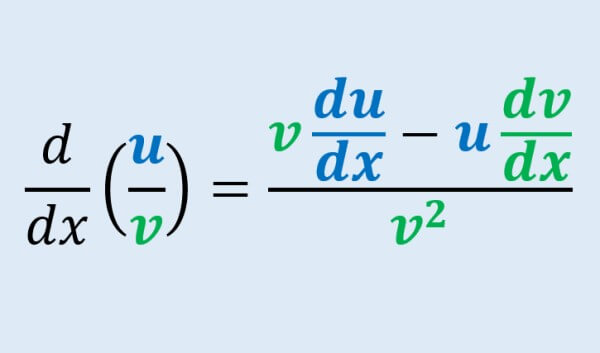
Relevante para…
Aprender sobre las diferentes demostraciones de la regla del cociente.
Demostración de la regla del cociente usando límites
Se recomienda que estés familiarizado con los temas La pendiente de una recta tangente y Derivadas usando límites, como requisitos previos para comprender mejor la demostración de la regla del cociente usando límites.
Podemos recordar que
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{f(x+h)-f(x)}{h}}$$
Ahora, vamos a utilizar la siguiente expresión:
$$\Upsilon(x) = \frac{f(x)}{g(x)}$$
Entonces, tenemos,
$$\Upsilon'(x) = \frac{d}{dx} \left(\frac{f(x)}{g(x)}\right)$$
Usando límites, podemos derivar $latex \Upsilon(x)$ por
$$\Upsilon'(x) = \lim \limits_{h \to 0} {\frac{\Upsilon(x+h)-\Upsilon(x)}{h}}$$
Sustituyendo la ecuación $latex \Upsilon(x) = \frac{f(x)}{g(x)}$, tenemos
$$\Upsilon'(x) = \lim \limits_{h \to 0} {\frac{{\frac{f(x+h)}{g(x+h)}} – {\frac{f(x)}{g(x)}}}{h}}$$
Obteniendo el mínimo común denominador del numerador, tenemos
$$\Upsilon'(x) = \lim \limits_{h \to 0} {\frac{\frac{f(x+h) \cdot g(x) – f(x) \cdot g(x+h)}{g(x+h) \cdot g(x)}}{h}}$$
Al aplicar las reglas de las fracciones, nuestra ecuación se puede reescribir como:
$$\Upsilon'(x) = \lim \limits_{h \to 0} {\frac{f(x+h) \cdot g(x) – f(x) \cdot g(x+h)}{g(x+h) \cdot g(x) \cdot h}}$$
Ahora, podemos sumar y restar el producto de f(x) y g(x), que es $latex f(x)g(x)$, al numerador $$f(x+h) \cdot g(x ) – f(x) \cdot g(x+h)g(x+h)$$
Por lo tanto, tenemos
$$\frac{d}{dx} \left(\frac{f(x)}{g(x)}\right) = \lim \limits_{h \to 0} {\frac{f(x+h) \cdot g(x) + f(x) \cdot g(x) – f(x) \cdot g(x) – f(x) \cdot g(x+h)}{g(x+h) \cdot g(x) \cdot h}}$$
Dado que $latex + f(x) \cdot g(x) – f(x) \cdot g(x) = 0$, no cambiamos la ecuación en absoluto.
Reordenando la ecuación anterior, tenemos
$$\frac{d}{dx} \left(\frac{f(x)}{g(x)}\right) = \lim \limits_{h \to 0} {\frac{f(x+h) \cdot g(x) – f(x) \cdot g(x) – f(x) \cdot g(x+h) + f(x) \cdot g(x)}{g(x+h) \cdot g(x) \cdot h}}$$
Ahora, podemos simplificar aún más la ecuación anterior factorizando el numerador:
$$\frac{d}{dx} \left(\frac{f(x)}{g(x)}\right) = \lim \limits_{h \to 0} {\frac{g(x) \cdot (f(x+h) – f(x)) – f(x) \cdot (g(x+h) – g(x))}{g(x+h) \cdot g(x) \cdot h}}$$
Entonces podemos reorganizar la ecuación de esta manera:
$$\frac{d}{dx} \left(\frac{f(x)}{g(x)}\right) = \lim \limits_{h \to 0} {\left(\frac{1}{g(x+h) \cdot g(x)}\right) \hspace{1.15 pt} \cdot \hspace{1.15 pt} \bigg[\left(g(x) \cdot \left(\frac{f(x+h) – f(x)}{h}\right)\right) – \hspace{1.15 pt} \left(f(x) \cdot \left(\frac{g(x+h) – g(x)}{h}\right)\right)\bigg]}$$
para que podamos manipularla algebraicamente de la manera necesaria para demostrar la regla del cociente.
Al aplicar las propiedades de los límites para resolver la ecuación, tenemos
$$\frac{d}{dx} \left(\frac{f(x)}{g(x)}\right) = \lim \limits_{h \to 0} {\frac{1}{g(x+h) \cdot g(x)}} \hspace{1.15 pt} \cdot \hspace{1.15 pt} \bigg[ \lim \limits_{h \to 0} {g(x)} \hspace{1.15 pt} \cdot \hspace{1.15 pt} \lim \limits_{h \to 0} {\frac{f(x+h) – f(x)}{h}} – \hspace{1.15 pt} \lim \limits_{h \to 0} {f(x)} \hspace{1.15 pt} \cdot \hspace{1.15 pt} \lim \limits_{h \to 0} {\frac{g(x+h) – g(x)}{h}} \bigg]$$
Entonces, podemos resolver los límites reconociendo que la primera parte de cada término es simplemente igual a las funciones $latex g(x)$ y $latex f(x)$ respectivamente y la segunda parte de cada término es la derivada en términos de límites de $latex f(x)$ y $latex g(x)$ respectivamente. Por lo tanto, tenemos:
$$ \frac{d}{dx}\left(\frac{f(x)}{g(x)}\right) = \left(\frac{1}{g(x) \cdot g(x)}\right) \hspace{1.15 pt} \cdot \hspace{1.15 pt} \Big[ \left( g(x) \cdot \frac{d}{dx}(f(x)) \right) – \hspace{1.15 pt} \left(f(x)\cdot \frac{d}{dx}(g(x)) \right) \Big]$$
Simplificando algebraicamente, tenemos
$$\frac{d}{dx}\left(\frac{f(x)}{g(x)}\right) = \frac{g(x) \cdot \frac{d}{dx}(f(x)) \hspace{1.15 pt} – \hspace{1.15 pt} f(x) \cdot \frac{d}{dx}(g(x))}{(g(x))^2}$$
o puede ser simplemente ilustrado como
$$\left(\frac{f}{g}\right)'(x) = \frac{g(x) \hspace{1.15 pt} \cdot \hspace{1.15 pt} f'(x) \hspace{2.3 pt} – \hspace{2.3 pt} f(x) \hspace{1.15 pt} \cdot \hspace{1.15 pt} g'(x)}{(g(x))^2}$$
que ahora es la fórmula de la regla del cociente.
Demostración de la regla del cociente usando las reglas del producto y de la cadena
Otra forma más fácil de demostrar y formular la regla del cociente es aplicando las fórmulas de las reglas del producto y de la cadena. Por lo tanto, se recomienda que se familiarice con los temas La fórmula de la regla de la cadena y La fórmula del producto como requisitos previos para comprender mejor esta prueba.
Podemos recordar que la fórmula de la regla del producto es
$latex (fg)'(x) = f(x) \cdot g'(x) + g(x) \cdot f'(x)$
Además de la regla del producto, también recordamos que la fórmula de la regla de la cadena es
$$\frac{d}{dx} [(f(x))^n] = n \cdot (f(x))^{n-1} \cdot \frac{d}{dx}(f(x))$$
Ahora, si tenemos dos funciones f(x) y g(x) y luego, se nos pide obtener la derivada de $latex \frac{f}{g}(x)$; tenemos
$$\left(\frac{f}{g}\right)’ (x) = \frac{d}{dx} \left(\frac{f(x)}{g(x)}\right)$$
Reescribiendo el denominador de la fracción en forma exponencial, tenemos
$$\frac{d}{dx} \left(\frac{f(x)}{g(x)}\right) = \frac{d}{dx} (f(x) \cdot (g(x))^{-1})$$
Ahora, podemos derivar el lado derecho de la ecuación aplicando la fórmula de la regla del producto:
$$\frac{d}{dx} \left(\frac{f(x)}{g(x)}\right) = f(x) \cdot \frac{d}{dx} (g(x))^{-1}) + (g(x))^{-1} \cdot \frac{d}{dx}(f(x))$$
Para derivar $latex \frac{d}{dx} (g(x))^{-1}$, necesitamos usar la fórmula de la regla de la cadena. Por lo tanto, tenemos
$$\frac{d}{dx} \left(\frac{f(x)}{g(x)}\right) = f(x) \cdot \left[(-1) \cdot (g(x))^{-2} \cdot \frac{d}{dx}(g(x)) \right]+ (g(x))^{-1} \cdot \frac{d}{dx}(f(x))$$
Realizando todas las operaciones aplicables, obteniendo el mínimo común denominador, reescribiendo el exponente negativo en forma fraccionaria y siguiendo las reglas de las fracciones, tenemos
$$\frac{d}{dx} \left(\frac{f(x)}{g(x)}\right) = f(x) \cdot \left[(-1) \cdot (g(x))^{-2} \cdot (g'(x)) \right]+ (g(x))^{-1} \cdot (f'(x))$$
$$\frac{d}{dx} \left(\frac{f(x)}{g(x)}\right) = -f(x) \cdot (g(x))^{-2} \cdot (g'(x)) + (g(x))^{-1} \cdot (f'(x))$$
$$ \frac{d}{dx} \left(\frac{f(x)}{g(x)}\right) = -f(x) \cdot \frac{1}{(g(x))^2} \cdot (g'(x)) + \frac{1}{g(x)} \cdot (f'(x))$$
$$\frac{d}{dx} \left(\frac{f(x)}{g(x)}\right) = \frac{-f(x) \cdot (g'(x))}{(g(x))^2} + \frac{(f'(x))}{g(x)}$$
$$\frac{d}{dx} \left(\frac{f(x)}{g(x)}\right) = -\frac{f(x) \cdot (g'(x))}{(g(x))^2} + \frac{g(x) \cdot (f'(x))}{(g(x))^2}$$
$$\frac{d}{dx} \left(\frac{f(x)}{g(x)}\right) = \frac{g(x) \cdot (f'(x))}{(g(x))^2} \hspace{1.15 pt} – \hspace{1.15 pt} \frac{f(x) \cdot (g'(x))}{(g(x))^2}$$
Entonces, finalmente, obtenemos
$$\left(\frac{f}{g}\right)'(x) = \frac{g(x) \hspace{1.15 pt} \cdot \hspace{1.15 pt} f'(x) \hspace{2.3 pt} – \hspace{2.3 pt} f(x) \hspace{1.15 pt} \cdot \hspace{1.15 pt} g'(x)}{(g(x))^2}$$
que es la fórmula de la regla del cociente.
Demostración de la regla del cociente usando diferenciación implícita
En realidad, este es el método más corto para demostrar la fórmula de la regla del cociente, considerando que estás familiarizado con los temas, la regla del producto y la diferenciación implícita.
Podemos recordar que la diferenciación implícita se usa para funciones en una forma más complicada en la que es difícil o imposible expresar f(x) o y explícitamente en términos de x. Por ejemplo, tenemos la ecuación:
$$y = \frac{u}{v}$$
y luego se nos pide derivar $latex y$. Derivando $latex y$, tenemos
$$y’ = \left(\frac{u}{v}\right)’$$
Pero suponiendo que no podemos simplificar más nuestra ecuación algebraicamente y aún no conocemos la fórmula de la regla del cociente, podemos derivarla aplicando la diferenciación implícita.
Para diferenciar implícitamente nuestra ecuación dada, primero debemos multiplicar algebraicamente en cruz el denominador del lado derecho al lado izquierdo de la ecuación. Por lo tanto, tenemos
$latex vy = u$
Luego, derivamos toda la ecuación en términos de la variable $latex x$:
$$\frac{d}{dx} (vy) = \frac{d}{dx} (u)$$
Para derivar el lado izquierdo de la ecuación, usaremos la regla del producto. También trataremos $latex v$ y $latex y$ como variables y no como constantes. Al hacerlo, tenemos
$$vy’ + yv’ = \frac{d}{dx} (u)$$
¿Cómo derivamos $latex u$ en términos de la variable $latex x$ en este caso? Al igual que $latex v$ y $latex y$, trataremos a $latex u$ como una variable, no como una constante. Al hacerlo, tenemos
$$vy’ + yv’ = u’$$
Dado que se nos pide obtener $latex y’$, debemos resolver nuestra ecuación en términos de $latex y’$. Al hacerlo, tenemos
$$y’ = \frac{u’-yv’}{v}$$
Pero, ¿qué es $latex y$? Podemos recordar que $latex y = \frac{u}{v}$. Sustituyendo $latex y$ en nuestra ecuación derivada, tenemos
$$y’ = \frac{u’-\left(\frac{u}{v}\right) \cdot v’}{v}$$
Al simplificar algebraicamente, obtener el mínimo común denominador y aplicar las reglas de las fracciones, tenemos
$$y’ = \frac{u’-\left(\frac{u}{v}\right) \cdot v’}{v}$$
$$y’ = \frac{u’-\left(\frac{uv’}{v}\right)}{v}$$
$$y’ = \frac{\left(\frac{vu’}{v}\right)-\left(\frac{uv’}{v}\right)}{v}$$
$$\frac{d}{dx}(\frac{u}{v}) = \frac{vu’ \hspace{2.3 pt} – \hspace{2.3 pt} uv’}{(v) \cdot (v)}$$
Entonces, finalmente, tenemos
| $latex \frac{d}{dx}(\frac{u}{v}) = \frac{vu’ \hspace{2.3 pt} – \hspace{2.3 pt} uv’}{v^2}$ |
que es la fórmula de la regla del cociente.
Veáse también
¿Interesado en aprender más sobre la regla del cociente? Echa un vistazo a estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
