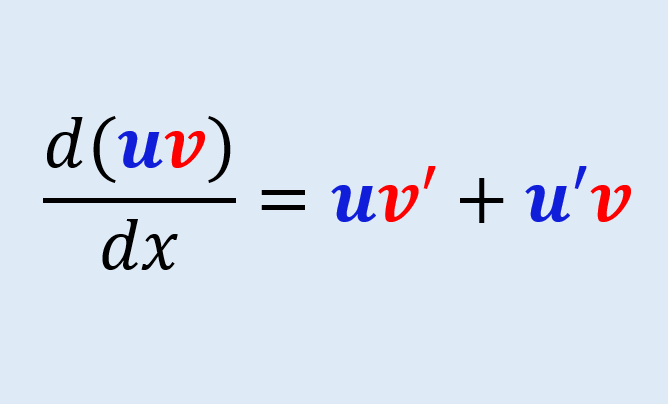La regla del producto es uno de los principios fundamentales que se aplican en el Cálculo Diferencial (o Cálculo I). Se usa comúnmente para derivar una función que involucra la operación de multiplicación. La regla del producto puede ser demostrada utilizando uno de los pilares del Cálculo, que son los límites.
En este artículo, exploraremos todo sobre la regla del producto. Cubriremos su definición, fórmula y aplicaciones. También veremos algunos ejemplos y problemas de práctica para aplicar los principios de la regla del producto.
La regla del producto y su fórmula
¿Qué es la regla del producto?
La regla del producto es una regla que establece que se puede derivar un producto de al menos dos funciones al obtener la suma de (a) primera función en forma original multiplicada por la derivada de la segunda función y (b) segunda función en forma original multiplicada por la derivada de la primera función.
La fórmula de la regla del producto
La fórmula de la regla del producto es:
$$(fg)'(x) = f(x) \cdot g'(x) + g(x) \cdot f'(x)$$
en donde
$latex u =$ primera función $latex f(x)$ o el primer multiplicando
$latex v =$ segunda función $latex g(x)$ o el segundo multiplicando
O en otras formas, puede ser:
$$\frac{d}{dx}(F(x)) = f(x) \cdot \frac{d}{dx}(g'(x)) + g(x) \cdot \frac{d}{dx}(f(x))$$
o
$$\frac{d}{dx}(uv) = uv’ + vu’$$
que es la forma más comúnmente utilizada de la fórmula de la regla del producto donde
$latex u = f(x)$
$latex v = g(x)$
y $latex \frac{d}{dx}(uv)$ también pueden ser $latex y’$, $latex F'(x)$, $latex{\Upsilon}’$ u otras letras utilizadas para denotar funciones con el símbolo de apóstrofo.
Echa un vistazo a nuestro artículo sobre las demostraciones de la regla del producto para aprender a demostrar la regla del producto paso a paso.
La regla del producto para tres o más funciones
Mira este artículo para conocer la regla del producto de tres o más funciones.
Cómo usar la regla del producto, un tutorial paso a paso
Supongamos que tenemos que derivar
$latex f(x) = x^2 \sin{(x)}$
Como puedes observar, esta función dada tiene dos multiplicandos, pero ya se pueden multiplicar algebraicamente ni simplificar. Entonces, podemos usar la regla del producto como se muestra en los siguientes pasos:
1. Identificar a los multiplicandos de la función dada.
En este caso, tenemos $latex u = x^2$ y $latex v = \sin{(x)}$.
2. Encontrar las derivadas de $latex u$ y $latex v$.
En este caso, tenemos $latex u’ = 2x$ y $latex v’ = \cos{(x)}$.
3. Aplicar la fórmula de la regla del producto.
$latex \frac{d}{dx}(uv) = uv’ + vu’$
$$\frac{d}{dx}(uv) = (x^2) \cdot (\cos{(x)}) + (\sin{(x)}) \cdot (2x)$$
4. Simplifica la derivada.
$latex \frac{d}{dx}(uv) = x^2 \cos{(x)} + 2x \sin{(x)}$
$latex f'(x) = x^2 \cos{(x)} + 2x \sin{(x)}$
Para propósitos de formalidad, se recomienda usar $latex f'(x), y’,$ o $latex \frac{d}{dx}(f(x))$ como su símbolo de derivadas en el lado izquierdo de la respuesta final en lugar de $latex (uv)’$ o $latex \frac{d}{dx}(uv)$.
Regla del producto – Ejemplos con respuestas
EJEMPLO 1
Deriva la siguiente función:
$latex f(x) = x^3 (x-5)$
Solución
Paso 1: En la forma elegida de la fórmula de la regla del producto de esta demostración, marcaremos el primer multiplicando como $latex u$ y el segundo multiplicando como $latex v$.
Entonces, tenemos
$latex u = x^3$
$latex v = (x-5)$
Paso 2: Deriva $latex u$ y $latex v$ individualmente:
$latex u’ = 3x$
$latex v’ = (1-0)$
Paso 3: Aplica la fórmula de la regla del producto ahora sustituyendo $latex u$, $latex u’$, $latex v$ y $latex v’$ en la fórmula de la regla del producto.
$latex \frac{d}{dx}(uv) = uv’ + vu’$
$$\frac{d}{dx}(uv) = (x^3) \cdot (1-0) + (x-5) \cdot (3x)$$
Paso 4: Simplifica algebraicamente:
$latex \frac{d}{dx}(uv) = x^3 + 3x (x-5)$
$latex \frac{d}{dx}(uv) = x^3 + 3x^2 – 15x$
$latex f'(x) = x^3 + 3x^2 – 15x$
EJEMPLO 2
Encuentra la derivada de la siguiente función:
$latex f(x) = \sin{(x)} \tan{(x)}$
Solución
Paso 1: En la forma elegida de la fórmula de la regla del producto de esta demostración, marcaremos el primer multiplicando como $latex u$ y el segundo multiplicando como $latex v$.
Entonces, tenemos
$latex u = \sin{(x)}$
$latex v = \tan{(x)}$
Paso 2: Deriva $latex u$ y $latex v$ individualmente:
$latex u’ = \cos{(x)}$
$latex v’ = \sec^{2}{(x)}$
Paso 3: Aplica la fórmula de la regla del producto ahora sustituyendo $latex u$, $latex u’$, $latex v$ y $latex v’$ en la fórmula de la regla del producto.
$latex \frac{d}{dx}(uv) = uv’ + vu’$
$$\frac{d}{dx}(uv) = (\sin{(x)}) \cdot (\sec^{2}{(x)})+ (\tan{(x)}) \cdot (\cos{(x)})$$
Paso 4: Simplifica algebraicamente y dado que tenemos una función trigonométrica en nuestra derivada, también podemos aplicar algunas identidades trigonométricas aplicables en nuestra solución:
$$\frac{d}{dx}(uv) = \sin{(x)} \sec^{2}{(x)} + \tan{(x)} \cos{(x)}$$
$$\frac{d}{dx}(uv) = (\sin{(x)}) (\frac{1}{\cos{(x)}})^2+ (\frac{\sin{(x)}}{\cos{(x)}}) (\cos{(x)})$$
$$\frac{d}{dx}(uv) = (\sin{(x)}) (\frac{1^{2}}{\cos^{2}{(x)}})+ (\frac{\sin{(x)}}{\cos{(x)}}) (\cos{(x)})$$
$$\frac{d}{dx}(uv) = (\frac{\sin{(x)}}{\cos{(x)}}) (\frac{1}{\cos{(x)}})+ (\frac{\sin{(x)}}{\cos{(x)}}) (\cos{(x)})$$
$$\frac{d}{dx}(uv) = \sec{(x)} \tan{(x)} + \sin{(x)}$$
$latex f'(x) = \sec{(x)} \tan{(x)} + \sin{(x)}$
EJEMPLO 3
Deriva la siguiente función:
$latex x^{2} \sin^{2}{(x)}$
Solución
Paso 1: Tenemos el primer multiplicando como $latex u$ y el segundo multiplicando como $latex v$.
Entonces, tenemos
$latex u = x^{2}$
$latex v = \sin^{2}{(x)}$
Paso 2: Deriva $latex u$ y $latex v$ individualmente:
$latex u’ = 2x$
$latex v’ = 2 \sin{(x)} \cos{(x)}$
Paso 3: Aplica la fórmula de la regla del producto ahora sustituyendo $latex u$, $latex u’$, $latex v$ y $latex v’$ en la fórmula de la regla del producto.
$latex \frac{d}{dx}(uv) = uv’ + vu’$
$$\frac{d}{dx}(uv) = x^{2} \cdot (2 \sin{(x)} \cos{(x)})+ (\sin^{2}{(x)}) \cdot (2x)$$
Paso 4: Simplifica algebraicamente y dado que tenemos una función trigonométrica en nuestra derivada, también podemos aplicar algunas identidades trigonométricas aplicables en nuestra solución:
$$\frac{d}{dx}(uv) = x^{2} \cdot (2 \sin{(x)} \cos{(x)})+ (\sin^{2}{(x)}) \cdot (2x)$$
$$\frac{d}{dx}(uv) = 2x^{2} \sin{(x)} \cos{(x)} + 2x \sin^{2}{(x)}$$
$$\frac{d}{dx}(uv) = x^{2} (2 \sin{(x)} \cos{(x)}) + 2x \sin^{2}{(x)}$$
$$\frac{d}{dx}(uv) = x^{2} \sin{(2x)} + 2x \sin^{2}{(x)}$$
$$\frac{d}{dx}(uv) = x^{2} \sin{(2x)} + 2x \sin^{2}{(x)}$$
EJEMPLO 4
¿Cuál es la derivada de $latex f(x) = 5x^7 \cot{(x^7)}$?
Solución
En este problema, tenemos dos multiplicandos en la función f(x). El primer multiplicando es $latex u=5x^7$ y el otro es $latex v=\cot{(x^7)}$
Por lo tanto, tenemos
$latex u = 5x^7$
$latex v = \cot{(x^7)}$
$latex f(x) = uv$
Ahora, podemos usar la fórmula de la regla del producto:
$latex f'(x) = uv’ + vu’$
$$\frac{d}{dx}f(x) = u \cdot \frac{d}{dx}(v) + v \cdot \frac{d}{dx}(u)$$
$$\frac{d}{dx}f(x) = 5x^7 \cdot \frac{d}{dx}(\cot{(x^7)}) + \cot{(x^7)} \cdot \frac{d}{dx}(5x^7)$$
Nota: La derivada de $latex u$ usa la fórmula de la regla de la potencia y la derivada de $latex v$ usa la fórmula de la regla de la cadena y la fórmula de la derivada para la función trigonométrica.
Al aplicar la fórmula de la regla del producto junto con las otras fórmulas derivadas que se usarán para $latex u’$ y $latex v’$, tenemos:
$$\frac{d}{dx}f(x) = 5x^7 \cdot (-7x^6 \csc^{2}{(x^7)}) + \cot{(x^7)} \cdot (35x^6)$$
Simplificando algebraicamente, obtenemos
$$ \frac{d}{dx}f(x) = -35x^{13} \csc^{2}{(x^7)} + 35x^6 \cot{(x^7)}$$
Y la respuesta final es:
$$f'(x) = 35x^6 \cot{(x^7)} – 35x^{13} \csc^{2}{(x^7)}$$
EJEMPLO 5
¿Cuál es la derivada de $latex f(x) = x^7 \sin{(\sin^{-1}{(x)})}$?
Solución
Aquí, el primer multiplicando es $latex u=x^7$ y el segundo multiplicando es $latex v=\sin{(\sin^{-1}{(x)})}$.
Por lo tanto, tenemos
$latex u = x^7$
$latex v = \sin{(\sin^{-1}{(x)})}$
$latex f(x) = uv$
Ahora, usamos la fórmula de la regla del producto para derivar nuestro problema dado:
$latex f'(x) = uv’ + vu’$
$$\frac{d}{dx}f(x) = u \cdot \frac{d}{dx}(v) + v \cdot \frac{d}{dx}(u)$$
$$\frac{d}{dx}f(x) = x^7 \cdot \frac{d}{dx}(\sin{(\sin^{-1}{(x)})})+ \sin{(\sin^{-1}{(x)})} \cdot \frac{d}{dx}(x^7)$$
Nota: En este problema, derivamos $latex u$ usando la fórmula de la regla de la potencia y derivamos $latex v$ usando las fórmulas de derivadas para la función trigonométrica y la función trigonométrica inversa.
Al aplicar la fórmula de la regla del producto junto con las otras fórmulas derivadas que se usarán para $latex u’$ y $latex v’$, tenemos:
$$\frac{d}{dx}f(x) = x^7 \cdot (\cos{(\sin^{-1}{(x)})} (\frac{1}{\sqrt{1-x^2}}))+ \sin{(\sin^{-1}{(x)})} \cdot (7x^6)$$
Simplificando algebraicamente y aplicando identidades y operaciones trigonométricas y trigonométricas inversas, obtenemos
$$\frac{d}{dx}f(x) = x^7 \cdot (1) + 7x^6 \cdot (x)$$
Y la respuesta final es:
$latex f'(x) = 8x^7$
Regla del producto – Problemas de práctica
Encuentra la derivada de la siguiente función y determina el valor de $latex F^{\prime}(0)$: $latex F(x) = \sin(x^2+2x)\cos(x)$?
Escribe la respuesta en la casilla.
Veáse también
¿Interesado en obtener más información sobre la regla del producto? Echa un vistazo a estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
