Demostración de la Regla del Producto de Derivadas

La Regla del Producto es una de las herramientas más útiles en Cálculo Diferencial (o Cálculo I) para derivar dos funciones que están siendo multiplicadas. Se puede usar junto con cualquier tipo de función existente siempre que las operaciones de multiplicación estén presentes en el problema de derivación dado.

Sin embargo, tan fácil como parece usar una fórmula estándar para derivar funciones con operaciones de multiplicación, es esencial aprender los conceptos detrás de esta fórmula estándar. Por lo tanto, aquí nos centraremos principalmente en las demostraciones de la fórmula de la regla del producto aplicando los conceptos de derivación mediante límites y la regla de la cadena.

CÁLCULO

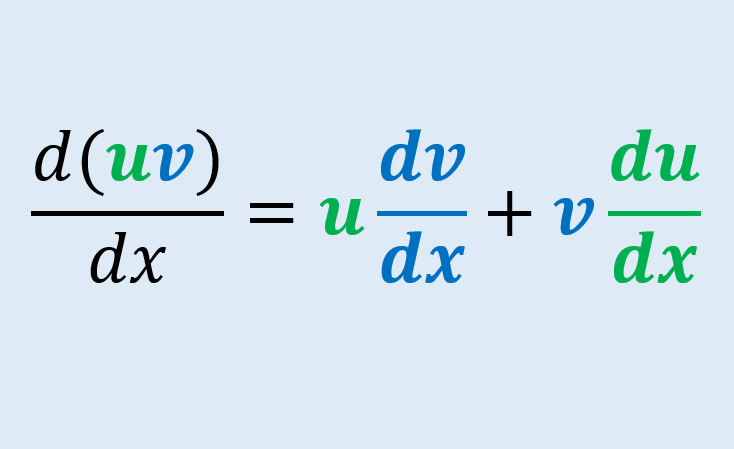
Fórmula para la regla del producto 2 de derivadas

Relevant for…

Conocer las diferentes demostraciones de la regla del producto.

Ver demostraciones

Contenidos

CÁLCULO

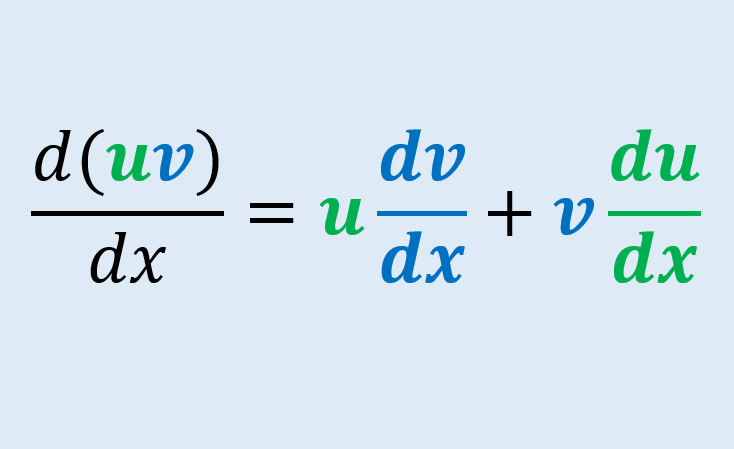
Relevante para…

Conocer las diferentes demostraciones de la regla del producto.

Ver demostraciones

¿Qué es la regla del producto?

La regla del producto se define como la derivada del producto de al menos dos funciones. La regla del producto se puede utilizar para derivar cualquier producto dado de funciones como:

$(fg)'(x) = \frac{d}{dx}(f(x) \cdot g(x))$

donde f(x) y g(x) pueden ser equivalentes a cualquier tipo de función.

Pero, ¿cómo derivamos exactamente esa función dada usando la regla del producto?

La regla del producto establece que la derivada de un producto de dos funciones es igual a la primera función f(x) en su forma original multiplicada por la derivada de la segunda función g(x) y luego sumada a la forma original de la segunda función g(x) multiplicada por la derivada de la primera función f(x).

Para ilustrarlo mejor, cuando queremos obtener la derivada de fg(x) o la derivada del producto de f(x) y g(x), tenemos:

(fg)'(x) = f(x) \cdot g'(x) + g(x) \cdot f'(x)

Fácil, ¿verdad? Pero no debemos tomar esta fórmula a la ligera si pretendemos poder derivar cualquier producto de funciones. Para aprender y comprender los conceptos detrás del desarrollo de esta fórmula de la regla del producto, debemos estar familiarizados con cualquier demostración que satisfaga la regla del producto.

→ Cursos Gratis: Explora Nuestros Cursos de Matemáticas

Demostración de la regla del producto usando límites

Para esta demostración, se recomienda que se familiarice con los temas La pendiente de una recta tangente y Derivadas usando límites, como requisitos previos para comprender mejor esta demostración.

Podemos recordar que

$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{f(x+h)-f(x)}{h}}$

Al aplicar límites, podemos derivar una función f(x). Pero, ¿qué tal un producto de dos funciones f(x) y g(x)?

Por ejemplo, nos tenemos dos funciones f(x) y g(x) y luego, se nos pide obtener la derivada de fg(x). Es decir, tenemos

$(fg)'(x) = \frac{d}{dx}(f(x) \cdot g(x))$

Para derivar el producto de estas dos funciones usando límites, supongamos que tenemos

$\Upsilon(x) = f(x) \cdot g(x)$

Entonces,

$\Upsilon'(x) = \frac{d}{dx}(f(x) \cdot g(x))$

y podemos derivar esto de la siguiente manera:

$\Upsilon'(x) = \lim \limits_{h \to 0} {\frac{\Upsilon(x+h)-\Upsilon(x)}{h}}$

Al sustituir la ecuación $\Upsilon(x) = f(x) \cdot g(x)$ , tenemos:

$\Upsilon'(x) = \lim \limits_{h \to 0} {\frac{f(x+h) \cdot g(x+h) - f(x) \cdot g(x)}{h}}$

lo cual puede ser escrito como:

$\frac{d}{dx}(f(x) \cdot g(x)) =$ $\lim \limits_{h \to 0} {\frac{f(x+h) \cdot g(x+h) - f(x) \cdot g(x)}{h}}$

Esto representa la derivada de un producto en términos de límites. Ahora, esta ecuación no se puede manipular algebraicamente fácilmente para llegar a la fórmula de la regla del producto que estamos tratando de demostrar.

Sin embargo, podemos sumar y restar $f(x+h) \cdot g(x)$ al numerador. Por lo tanto, tenemos

$\frac{d}{dx}(f(x) \cdot g(x)) =$ $\lim \limits_{h \to 0} {\frac{f(x+h) \cdot g(x+h) - f(x+h) \cdot g(x) + f(x+h) \cdot g(x) - f(x) \cdot g(x)}{h}}$

Dado que $+ f(x+h) \cdot g(x) - f(x+h) \cdot g(x) = 0$ , no cambiamos la expresión en absoluto.

Ahora, podemos factorizar $f(x+h)$ de los dos primeros términos y $g(x)$ de los dos últimos términos. Entonces, podemos dividir la expresión en dos partes y, simplificando, tenemos,

$\frac{d}{dx}(f(x) \cdot g(x)) = \lim \limits_{h \to 0} {\frac{f(x+h) \cdot (g(x+h)-g(x))}{h}$ $+\lim \limits_{h \to 0} \frac{g(x) \cdot (f(x+h)-f(x))}{h}}$

$\frac{d}{dx}(f(x) \cdot g(x)) = \lim \limits_{h \to 0} {f(x+h) \cdot \frac{g(x+h)-g(x)}{h}$ $+\lim \limits_{h \to 0} g(x) \cdot \frac{f(x+h)-f(x)}{h}}$

Al aplicar las propiedades de los límites para resolver la ecuación, tenemos

$\frac{d}{dx}(f(x) \cdot g(x)) = \lim \limits_{h \to 0} {f(x+h)} \cdot \lim \limits_{h \to 0} {\frac{g(x+h)-g(x)}{h}}$ $+ \lim \limits_{h \to 0} {g(x)} \cdot \lim \limits_{h \to 0} {\frac{f(x+h)-f(x)}{h}}$

Los límites $\lim \limits_{h \to 0} {f(x+h)}$ y $\lim \limits_{h \to 0} {g(x)}$ pueden resolverse fácilmente. Cuando h tiende a cero, simplemente obtendremos $f(x)$ y $g(x)$ respectivamente.

Los límites $\lim \limits_{h \to 0} {\frac{g(x+h)-g(x)}{h}}$ y $\lim \limits_{h \to 0} {\ frac{f(x+h)-f(x)}{h}}$ parecen más complicados, pero son simplemente las derivadas de $g(x)$ y $h(x)$ expresadas en límites. Por lo tanto, tenemos:

$\frac{d}{dx}(f(x) \cdot g(x)) = f(x) \cdot \frac{d}{dx}(g(x))$ $+ g(x) \cdot \frac{d}{dx}(f(x))$

o podemos expresar esto simplemente como

$(fg)'(x) = f(x) \cdot g'(x) + g(x) \cdot f'(x)$

que ahora es la fórmula de la regla del producto.

Demostración de la regla del producto usando la regla de la cadena

Este método de demostración hace que la regla del producto sea más fácil de probar y formular. Por lo tanto, se recomienda que se familiarice con los temas La fórmula de la regla de la cadena, La suma/diferencia de derivadas y La fórmula de la potencia como requisito previos para comprender mejor esta demostración.

Podemos recordar que la fórmula de la regla de la cadena es

$\frac{d}{dx}[(f(x))^n] = n \cdot (f(x))^{n-1} \cdot \frac{d}{dx}(f(x))$

Para facilitar la derivación de la regla del producto, podemos considerar la siguiente expresión:

$\Upsilon(x) = {{(f+g)}^2}$

donde f y g son dos funciones válidas.

Vamos a derivar $\Upsilon(x)$ aplicando la regla de la cadena. Por lo tanto, tenemos:

$\Upsilon'(x)= 2(f+g)(f'+g')$

Si multiplicamos y expandimos los paréntesis, tenemos:

$\Upsilon'(x)= 2(ff'+fg'+gf'+gg')$

$= 2ff'+2fg'+2gf'+2gg'$

Ahora, en lugar de usar la regla de la cadena, podemos expandir la expresión ${{(f+g)}^2}$ para obtener:

$\Upsilon(x) = {{f}^2}+fg+{{g}^2}$

Si diferenciamos término por término, obtenemos:

$\Upsilon'(x)= 2ff'+2(fg)'+2gg')$

Como las dos expresiones que obtuvimos para $\Upsilon'(x)$ son equivalentes, tenemos:

$2ff'+2(fg)'+2gg')= 2ff'+2fg'+2gf'+2gg'$

$(fg)'= fg'+gf'$

Claramente hemos llegado a la regla del producto.

Demostración de la regla del producto usando diferenciación logarítmica

Un tercer método que podemos usar para demostrar la regla del producto es usar la diferenciación logarítmica y la diferenciación implícita. Este es un método más rápido pero requiere que esté familiarizado con ambos temas.

Podemos empezar escribiendo la siguiente expresión:

$y=f(x)g(x)$

Ahora, podemos tomar el logaritmo natural de ambos lados:

$\ln(y)=\ln(f(x)g(x))$

Usando las leyes de los logaritmos en el lado derecho, podemos escribir:

$\ln(y)=\ln f(x)+\ln g(x)$

Tomando la derivada de ambos lados, tenemos:

$\frac{y'}{y}=\frac{f'(x)}{f(x)}+\frac{g'(x)}{g(x)}$

Resolviendo para $y'$ , tenemos:

$y'=y\left(\frac{f'(x)}{f(x)}+\frac{g'(x)}{g(x)}\right)$

Ahora, podemos sustituir $y=f(x)g(x)$ para obtener:

$(fg)'=f(x)g(x)\left(\frac{f'(x)}{f(x)}+\frac{g'(x)}{g(x)}\right)$

Si multiplicamos y expandimos los paréntesis, obtenemos:

$(fg)'=g(x)f'(x)+f(x)g'(x)$

Hemos llegado a la regla del producto.

Únete a nuestros cursos interactivos o practica con nuestros generadores de problemas

Regla del producto – Ejemplos con respuestas

EJEMPLO 1

Derive lo siguiente:

$f(x) = \sqrt[5]{x^3} \cdot (x^5 + 3x^2 - 4x)$

Solución

Lo primero que debemos hacer es escribir la fórmula de la regla del producto para nuestra referencia:

$\frac{d}{dx}(uv) = uv' + vu'$

Tenemos dos multiplicandos en la función dada f(x). El primer multiplicando es $\sqrt[5]{x^3}$ y el otro es $(x^5 + 3x^2 - 4x)$ .

Con base en la fórmula de la regla del producto, $u$ es el primer multiplicando y $v$ es el segundo multiplicando.

Por lo tanto, tenemos

$u = \sqrt[5]{x^3}$
$v = (x^5 + 3x^2 - 4x)$
$f(x) = uv$

Ahora, podemos usar la fórmula de la regla del producto para derivar nuestro problema dado:

$f'(x) = uv' + vu'$

$\frac{d}{dx}f(x) = u \cdot \frac{d}{dx}(v) + v \cdot \frac{d}{dx}(u)$

$\frac{d}{dx}f(x) = (\sqrt[5]{x^3}) \cdot \frac{d}{dx}(x^5 + 3x^2 - 4x)$ $+ (x^5 + 3x^2 - 4x) \cdot \frac{d}{dx}(\sqrt[5]{x^3})$

Para cualquier radical, es recomendable reescribirlos en forma de exponente fraccionario:

$\frac{d}{dx}f(x) = (x^3)^{\frac{1}{5}} \cdot \frac{d}{dx}(x^5 + 3x^2 - 4x)$ $+ (x^5 + 3x^2 - 4x) \cdot \frac{d}{dx}((x^3)^{\frac{1}{5}})$

Nota: En este problema, la derivada de $u$ utilizará la regla de la cadena y la fórmula de la regla de la potencia, mientras que la derivada de $v$ utilizará la fórmula de la regla de la potencia y la suma/diferencia de derivadas.

Al aplicar la fórmula de la regla del producto junto con las otras fórmulas derivadas que se usarán para $\textbf{\emph{u'}}$ y $\textbf{\emph{v'}}$ , tenemos:

$\frac{d}{dx}f(x) = (x^3)^{\frac{1}{5}} \cdot (5x^4 + 6x - 4)$ $+ (x^5 + 3x^2 - 4x) \cdot (\frac{1}{5} \cdot (x^3)^{-\frac{4}{5}} \cdot 3x^2)$

Simplificando algebraicamente, obtenemos

$f'(x) = x^{\frac{3}{5}} \cdot (5x^4 + 6x - 4)$ $+ (x^5 + 3x^2 - 4x) \cdot (\frac{3}{5}x^{-\frac{2}{5}})$

$f'(x) = 5x^{\frac{23}{5}} + 6x^{\frac{8}{5}} - 4x^{\frac{3}{5}}$ $+ \frac{3}{5}x^{\frac{23}{5}} + \frac{9}{5}x^{\frac{8}{5}} - \frac{12}{5}x^{\frac{3}{5}}$

$f'(x) = \frac{28}{5}x^{\frac{23}{5}} + \frac{39}{5}x^{\frac{8}{5}} - \frac{32}{5}x^{\frac{3}{5}}$

Y la respuesta final es:

$f'(x) = \frac{28x^{\frac{23}{5}} + 39x^{\frac{8}{5}} - 32x^{\frac{3}{5}}}{5}$

O en forma radical,

$f'(x) = \frac{28\sqrt[5]{x^{23}} + 39\sqrt[5]{x^8} - 32\sqrt[5]{x^3}}{5}$

EJEMPLO 2

Derive la siguiente función:

$f(x) = (5x^5-x^4) \cdot (30x-12x^2)$

Solución

Basado en lo dado, tenemos dos multiplicandos en la función dada f(x). El primer multiplicando es $(5x^5-x^4)$ y el otro es $(30x-12x^2)$ .

Si $u$ es el primer multiplicando y $v$ es el segundo multiplicando, tenemos

$u = (5x^5-x^4)$
$v = (30x-12x^2)$
$f(x) = uv$

Ahora, podemos usar la fórmula de la regla del producto para derivar nuestro problema dado:

$f'(x) = uv' + vu'$

$\frac{d}{dx}f(x) = u \cdot \frac{d}{dx}(v) + v \cdot \frac{d}{dx}(u)$

$\frac{d}{dx}f(x) = (5x^5-x^4) \cdot \frac{d}{dx}(30x-12x^2)$ $+ (30x-12x^2) \cdot \frac{d}{dx}(5x^5-x^4)$

Nota: En este problema, la derivada de $u$ usará la fórmula de la regla de la potencia y la suma/diferencia de derivadas. La derivada de $v$ también usará las mismas fórmulas de derivación usadas en $u$ .

Al aplicar la fórmula de la regla del producto junto con las otras fórmulas derivadas que se usarán para $\textbf{\emph{u'}}$ y $\textbf{\emph{v'}}$ , tenemos:

$\frac{d}{dx}f(x) = (5x^5-x^4) \cdot (30-24x)$ $+ (30x-12x^2) \cdot (25x^4-4x^3)$

Simplificando algebraicamente, obtenemos

$f'(x) = [-120x^6+174x^5-30x^4]$ $+ [-300x^6+798x^5-120x^4]$

$f'(x) = -120x^6-300x^6$ $+174x^5+798x^5-30x^4-120x^4$

Y la respuesta final es:

$f'(x) = -420x^6+972x^5-150x^4$

EJEMPLO 3

¿Cuál es la derivada de la siguiente función?

$f(x) = 6x^3 \cdot \ln{(x)}$

Solución

Tenemos dos multiplicandos en la función dada f(x). El primer multiplicando es $6x^3$ y el otro es $\ln{(x)}$ .

Basándonos en la fórmula de la regla del producto, y teniendo a $u$ como el primer multiplicando y $v$ el segundo multiplicando, tenemos

$u = 6x^3$
$v = \ln{(x)}$
$f(x) = uv$

Ahora, podemos usar la fórmula de la regla del producto para derivar nuestro problema dado:

$f'(x) = uv' + vu'$

$\frac{d}{dx}f(x) = u \cdot \frac{d}{dx}(v) + v \cdot \frac{d}{dx}(u)$

$\frac{d}{dx}f(x) = 6x^3 \cdot \frac{d}{dx}(\ln{(x)}) + \ln{(x)} \cdot \frac{d}{dx}(6x^3)$

Nota: En este problema, la derivada de $u$ utilizará la fórmula de la regla de la potencia, mientras que la derivada de $v$ utilizará la fórmula de la derivada para funciones logarítmicas.

Al aplicar la fórmula de la regla del producto junto con las otras fórmulas derivadas que se usarán para $\textbf{\emph{u'}}$ y $\textbf{\emph{v'}}$ , tenemos:

$\frac{d}{dx}f(x) = 6x^3 \cdot (\frac{1}{x}) + \ln{(x)} \cdot (18x^2)$

Simplificando algebraicamente, obtenemos

$f'(x) = 6x^2 + 18x^2 \cdot \ln{(x)}$

Y la respuesta final es:

$f'(x) = 6x^2 + 18x^2\ln{(x)}$

EJEMPLO 4

Encuentra la derivada de:

$f(x) = 9x^3 \cdot \sec{(\pi x)}$

Solución

Tenemos dos multiplicandos en la función dada f(x). El primer multiplicando es $6x^3$ y el otro es $\ln{(x)}$ .

Basándonos en la fórmula de la regla del producto, y teniendo a $u$ como el primer multiplicando y $v$ como el segundo multiplicando, tenemos

$u = 9x^3$
$v = \sec{(\pi x)}$
$f(x) = uv$

Ahora, podemos usar la fórmula de la regla del producto para derivar nuestro problema dado:

$f'(x) = uv' + vu'$

$\frac{d}{dx}f(x) = u \cdot \frac{d}{dx}(v) + v \cdot \frac{d}{dx}(u)$

$\frac{d}{dx}f(x) = 9x^3 \cdot \frac{d}{dx}(\sec{(\pi x)})$ $+ \sec{(\pi x)} \cdot \frac{d}{dx}(9x^3)$

Nota: En este problema, la derivada de $u$ utilizará la fórmula de la regla de la potencia, mientras que la derivada de $v$ utilizará la fórmula de la regla de la cadena y la fórmula de la derivada para funciones trigonométricas.

Al aplicar la fórmula de la regla del producto junto con las otras fórmulas derivadas que se usarán para $\textbf{\emph{u'}}$ y $\textbf{\emph{v'}}$ , tenemos:

$\frac{d}{dx}f(x) = 9x^3 \cdot (\pi \sec{(\pi x)} \tan{(\pi x)})$ $+ \sec{(\pi x)} \cdot (27x^2)$

Simplificando algebraicamente, obtenemos

$f'(x) = 9\pi x^3 \cdot (\sec{(\pi x)} \tan{(\pi x)})$ $+ 27x^2 \cdot \sec{(\pi x)}$

Y la respuesta final es:

$f'(x) = 9\pi x^3 \sec{(\pi x)} \tan{(\pi x)}$ $+ 27x^2 \sec{(\pi x)}$

EJEMPLO 5

Derive la siguiente función:

$f(x) = 5^x \cdot (x+5)^5$

Solución

Tenemos dos multiplicandos en la función dada f(x). El primer multiplicando es $5^x$ y el otro es $(x+5)^5$ .

Si $u$ es el primer multiplicando y $v$ el segundo multiplicando, tenemos

$u = 5^x$
$v = (x+5)^5$
$f(x) = uv$

Ahora, podemos usar la fórmula de la regla del producto para derivar nuestro problema dado:

$f'(x) = uv' + vu'$

$\frac{d}{dx}f(x) = u \cdot \frac{d}{dx}(v) + v \cdot \frac{d}{dx}(u)$

$\frac{d}{dx}f(x) = 5^x \cdot \frac{d}{dx}((x+5)^5)$ $+ (x+5)^5 \cdot \frac{d}{dx}(5^x)$

Nota: En este problema, la derivada de $u$ utilizará la fórmula de la derivada para la función exponencial, mientras que la derivada de $v$ utilizará la fórmula de la regla de la cadena.

Al aplicar la fórmula de la regla del producto junto con las otras fórmulas derivadas que se usarán para $\textbf{\emph{u'}}$ y $\textbf{\emph{v'}}$ , tenemos:

$\frac{d}{dx}f(x) = 5^x \cdot (5 \cdot (x+5)^4 \cdot (1))$ $+ (x+5)^5 \cdot (5^x \cdot \ln{(5)} \cdot (1))$