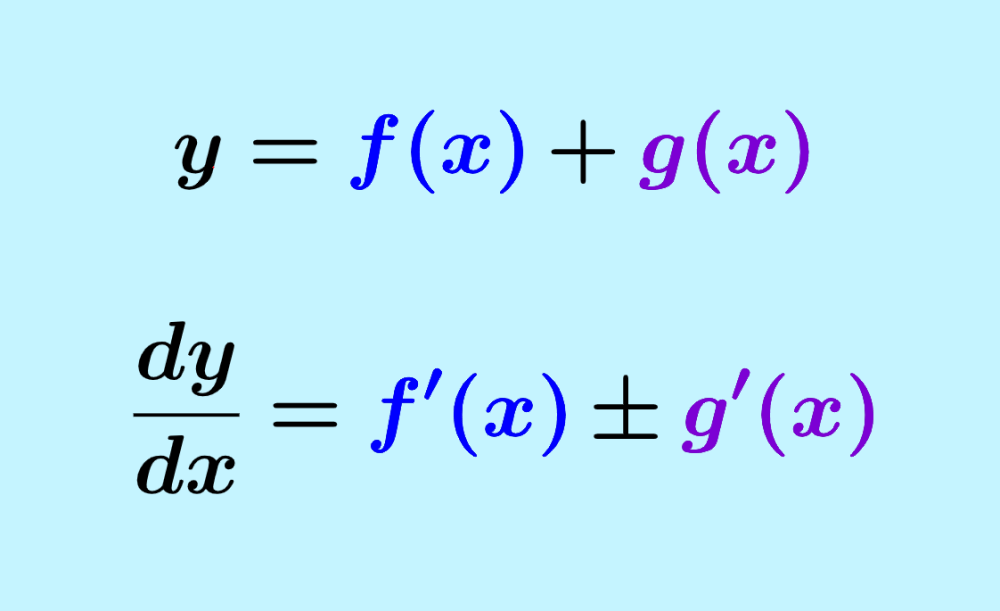Para derivar una suma o resta de funciones, tenemos que derivar a cada término de la función separadamente. Esto significa que podemos simplemente aplicar la regla de la potencia u otra regla relevante para derivar cada término y encontrar la derivada de toda la función.
A continuación, resolveremos 10 ejercicios de derivadas de la suma y resta de funciones. Además, exploraremos 5 problemas para practicar la derivación de estas funciones.
CÁLCULO
Relevante para…
Resolver ejercicios de derivadas de la suma y resta de funciones.
CÁLCULO
Relevante para…
Resolver ejercicios de derivadas de la suma y resta de funciones.
Definición y fórmula de la regla de la suma y resta de funciones en derivadas
La regla de las derivadas de una suma o resta de funciones nos dice que cuando $latex y$ está formada de más de una función, podemos encontrar su derivada al diferenciar a cada función una por una.
La regla de la suma y de la resta de funciones en derivadas nos permite encontrar la derivada de funciones como la siguiente:
$latex y=f(x)+g(x)$
Entonces, su derivada es igual a:
$$\frac{dy}{dx}=f'(x) \pm g'(x)$$
Esto aplica a la suma o diferencia de cualquier número de funciones.
Para derivar a cada una de las funciones o cada uno de los términos, usamos la regla de la potencia, $latex \frac{d}{dx}(x^n) = nx^{n-1}$, o cualquier otra regla de derivadas aplicable.
Pasos para derivar una suma o resta de dos o más funciones
Supongamos que tenemos que derivar
$latex f(x) = x^2+5x$
Tenemos una función que es una suma de dos términos. Entonces, podemos derivarla siguiendo los siguientes pasos:
1. Usar las leyes de los exponentes para transformar a radicales o expresiones racionales a la forma exponencial.
En este caso, no tenemos radicales o expresiones racionales. Nota: Un ejemplo sería escribir a $latex \sqrt{x}$ como $latex x^{\frac{1}{2}}$.
2. Aplica la fórmula de la regla de la potencia, $latex \frac{d}{dx}(x^n) = nx^{n-1}$, u otras reglas aplicables a cada término de la suma o resta:
$$f'(x) = 2x+5$$
3. Simplifica la expresión resultante.
En este caso, ya no podemos simplificar. Nota: Un ejemplo sería escribir a $latex x^{-\frac{1}{2}}$ como $latex \frac{1}{\sqrt{x}}$.
Puedes usar $latex f'(x), y’,$ o $latex \frac{d}{dx}(f(x))$ como símbolo de derivada en el lado izquierdo de la respuesta final.
10 Ejercicios de derivadas de suma y resta de funciones resueltos
EJERCICIO 1
Encuentra la derivada de $latex f(x)=x^4+5x$.
Solución
Paso 1: Empezamos convirtiendo expresiones radicales o racionales a su forma exponencial. En este caso, no tenemos radicales ni variables escritas en forma racional.
Paso 2: Usamos la fórmula de la regla de la potencia, $latex \frac{d}{dx}(x^n) = nx^{n-1}$, para derivar ambos términos de la función:
$latex f(x)=x^4+5x$
$latex f'(x)=4(x^{4-1})+5(x^{1-1})$
$latex f'(x)=4x^3+5$
Paso 3: Simplificamos si es que es posible. En este caso, no.
EJERCICIO 2
¿Cuál es la derivada de la función $latex f(x)=-5x^3+10x^2$?
Solución
Paso 1: La función no tiene radicales o expresiones racionales.
Paso 2: Vamos a derivar usando la regla de la potencia, $latex \frac{d}{dx}(x^n) = nx^{n-1}$, para derivar ambos términos de la función:
$latex f(x)=-5x^3+10x^2$
$latex f(x)=3(-5x^{3-1})+2(10x^{2-1})$
$latex f'(x)=-15x^2+20x$
Paso 3: La función ya está simplificada.
EJERCICIO 3
Encuentra la derivada de la función $latex f(x)=7x^8+5x^{-3}$.
Solución
Paso 1: Los dos términos tienen variables con exponentes numéricos.
Paso 2: Tenemos un exponente negativo, pero simplemente usamos la regla de la potencia para derivar ambos términos:
$latex f(x)=7x^8+5x^{-3}$
$latex f(x)=8(7x^{8-1})+(-3)(5x^{-3-1})$
$latex f'(x)=56x^7-15x^{-4}$
Paso 3: Usando las leyes de los exponentes, podemos escribir de la siguiente forma:
$$f'(x)=56x^7-\frac{15}{x^4}$$
EJERCICIO 4
Encuentra la derivada de la función $latex f(x)=3x^{-5}-2x^{-2}$.
Solución
Paso 1: Tenemos exponentes negativos, pero no hay radicales o variables con expresiones racionales.
Paso 2: Usamos la fórmula de la regla de la potencia, $latex \frac{d}{dx}(x^n) = nx^{n-1}$, para derivar ambos términos de la función:
$latex f(x)=3x^{-5}-2x^{-2}$
$latex f(x)=-5(3x^{-5-1})-2(-2x^{-2-1})$
$latex f'(x)=-15x^{-6}+4x^{-3}$
Paso 3: Usamos las leyes de los exponentes para simplificar:
$$f'(x)=-\frac{15}{x^6}+\frac{4}{x^3}$$
EJERCICIO 5
¿Cuál es la derivada de la función $latex f(x)=-5x^4+ \frac{1}{x}$?
Solución
Paso 1: Usando las leyes de los exponentes, podemos escribir de la siguiente forma:
$latex f(x)=-5x^4+ x^{-1}$
Paso 2: Ahora que solo tenemos exponentes numéricos, usamos la fórmula de la regla de la potencia, $latex \frac{d}{dx}(x^n) = nx^{n-1}$, en ambos términos de la función:
$latex f(x)=-5x^4+ x^{-1}$
$latex f'(x)=-20x^3-x^{-2}$
Paso 3: Con las leyes de los exponentes, podemos escribir de la siguiente forma:
$$f'(x)=-20x^3-\frac{1}{x^2}$$
EJERCICIO 6
¿Cuál es la derivada de $latex f(x)=4x^3+2x^2+\frac{2}{x^3}$?
Solución
Paso 1: Empezamos convirtiendo la expresión racional a una expresión con un exponente numérico:
$latex f(x)=4x^3+2x^2+2x^{-3}$
Paso 2: Usando la regla de la potencia para los tres términos, tenemos:
$latex f(x)=4x^3+2x^2+2x^{-3}$
$latex f'(x)=12x^2+4x-6x^{-4}$
Paso 3: Usamos las leyes de los exponentes nuevamente para escribir de la siguiente forma:
$$f'(x)=12x^2+4x-\frac{6}{x^4}$$
EJERCICIO 7
Determina la derivada de $latex f(x)=3x^2+\frac{2}{3x^2}+ x^{ \frac{1}{2}}$.
Solución
Paso 1: Usamos las leyes de los exponentes para escribir a la función así:
$$f(x)=3x^2+\frac{2}{3}x^{-2}+ x^{-\frac{1}{2}}$$
Paso 2: Usando la regla de la potencia en los tres términos de la función, tenemos:
$$f(x)=3x^2+\frac{2}{3}x^{-2}+ x^{-\frac{1}{2}}$$
$$f'(x)=6x-\frac{4}{3}x^{-3}-\frac{1}{2}x^{-\frac{3}{2}}$$
Paso 3: Simplificamos al escribir de la siguiente forma:
$$f'(x)=6x-\frac{4}{3x^3}-\frac{1}{2x^{\frac{3}{2}}}$$
$$f'(x)=6x-\frac{4}{3x^3}-\frac{1}{2\sqrt{x^3}}$$
EJERCICIO 8
Encuentra la derivada de la función $latex f(x)=\sqrt{x}+ \frac{3}{x^3} $.
Solución
Paso 1: Aplicando las leyes de los exponentes, podemos escribir de la siguiente forma:
$$f(x)=x^{\frac{1}{2}}+3x^{-3}$$
Paso 2: Aplicamos la regla de la potencia para derivar ambos términos:
$$f(x)=x^{\frac{1}{2}}+3x^{-3}$$
$$f'(x)=\frac{1}{2}x^{-\frac{1}{2}}-9x^{-4}$$
Paso 3: Usando las leyes de los exponentes nuevamente, podemos escribir de la siguiente forma:
$$f'(x)=\frac{1}{2x^{\frac{1}{2}}}-\frac{9}{x^4}$$
$$f'(x)=\frac{1}{2\sqrt{x}}-\frac{9}{x^4}$$
EJERCICIO 9
Encuentra la derivada de $latex f(x)=5x^{-5}+\frac{1}{\sqrt{x}}$.
Solución
Paso 1: Empezamos escribiendo de la siguiente forma:
$$f(x)=5x^{-5}+x^{-\frac{1}{2}}$$
Paso 2: Derivando ambos términos con la regla de la potencia, tenemos:
$$f(x)=5x^{-5}+x^{-\frac{1}{2}}$$
$$f'(x)=-25x^{-6}-\frac{1}{2}x^{-\frac{3}{2}}$$
Paso 3: Simplificamos a la expresión resultante usando las leyes de los exponentes:
$$f'(x)=-\frac{25}{x^6}-\frac{1}{2x^{\frac{3}{2}}}$$
$$f'(x)=-\frac{25}{x^6}-\frac{1}{2\sqrt{x^3}}$$
EJERCICIO 10
Determina la derivada de $latex f(x)=\frac{2}{3x^2}+ \frac{1}{\sqrt[3]{x^2}}- \frac{5}{x}$.
Solución
Paso 1: Empezamos usando las leyes de los exponentes para escribir así:
$$f(x)=\frac{2}{3}x^{-2}+ x^{\frac{2}{3}}- 5x^{-1}$$
Paso 2: Usamos la regla de la potencia para derivar a los términos:
$$f(x)=\frac{2}{3}x^{-2}+ x^{\frac{2}{3}}- 5x^{-1}$$
$$f'(x)=-\frac{4}{3}x^{-3}+ \frac{2}{3}x^{-\frac{1}{3}}+ 5x^{-2}$$
Paso 3: Finalmente, simplificamos de la siguiente forma:
$$f'(x)=-\frac{4}{3x^3}+ \frac{2}{3x^{\frac{1}{3}}}+ \frac{5}{x^2}$$
$$f'(x)=-\frac{4}{3x^3}+ \frac{2}{3\sqrt[3]{x}}+ \frac{5}{x^2}$$
Ejercicios de derivadas de suma y resta de funciones para resolver
Encuentra el valor de $latex f'(5)$ si es que tenemos la siguiente función: $$f(x)=4x^3-6x^2+3x-10$$
Escribe el resultado en la casilla.
Véase también
¿Interesado en aprender más sobre derivadas? Puedes mirar estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
