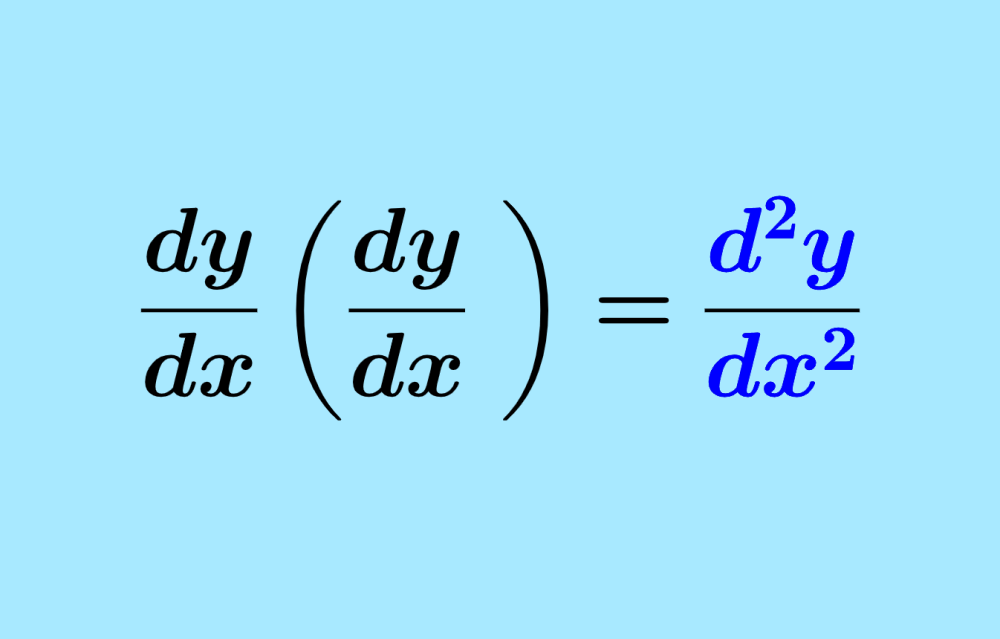Segunda derivada de una función – Ejercicios resueltos

Para encontrar la segunda derivada, tenemos que empezar encontrando la primera derivada de la función. Entonces, derivamos usando la regla de la potencia de derivadas:

$latex f(x)=5x^3$

$latex f'(x)=15x^2$

Ahora, usamos la regla de la potencia nuevamente para derivar a $latex f'(x)$:

$latex f'(x)=15x^2$

$latex f^{\prime \prime}(x)=30x$

La segunda derivada es $latex f^{\prime \prime}(x)=30x$.

Podemos usar la regla de la potencia de derivadas en cada término de la función para encontrar la primera derivada:

$latex f(x)=4x^4-2x^2+7x$

$latex f'(x)=16x^3-4x+7$

Vamos a derivar a $latex f'(x)$ para encontrar la segunda derivada usando el mismo método:

$latex f'(x)=16x^3-4x+7$

$latex f^{\prime \prime}(x)=48x^2-4$

Tenemos una expresión racional. Entonces, podemos usar las leyes de los exponentes para escribir de la siguiente forma:

$$f(x)=5x^6+\frac{3}{x}$$

$latex f(x)=5x^6+3x^{-1}$

Ahora que solo tenemos exponentes numéricos, usamos la regla de la potencia para derivar:

$latex f(x)=5x^6+3x^{-1}$

$latex f'(x)=30x^5-3x^{-2}$

Al derivar a $latex f'(x)$, tenemos:

$latex f'(x)=30x^5-3x^{-2}$

$latex f^{\prime \prime}(x)=150x^4+6x^{-3}$

Usando las leyes de los exponentes, podemos escribir de la siguiente forma:

$latex f^{\prime \prime}(x)=150x^4+6x^{-3}$

$$f^{\prime \prime}(x)=150x^4+\frac{6}{x^3}$$

Podemos escribir a la raíz cuadrada como un exponente numérico:

$$f(x) = -3x^{-5}+\sqrt{x}$$

$$f(x)=-3x^{-5}+x^{\frac{1}{2}}$$

Ahora, podemos encontrar la primera derivada de la siguiente forma:

$$f(x)=-3x^{-5}+x^{\frac{1}{2}}$$

$$f'(x)=15x^{-6}+\frac{1}{2}x^{-\frac{1}{2}}$$

Encontramos la segunda derivada al derivar a $latex f'(x)$:

$$f'(x)=15x^{-6}+\frac{1}{2}x^{-\frac{1}{2}}$$

$$f^{\prime \prime}(x)=-90x^{-7}-\frac{1}{4}x^{-\frac{3}{2}}$$

Podemos simplificar al usar las leyes de los exponentes y escribir de la siguiente forma:

$$f^{\prime \prime}(x)=-90x^{-7}-\frac{1}{4}x^{-\frac{3}{2}}$$

$$f^{\prime \prime}(x)=-\frac{90}{x^7}-\frac{1}{4\sqrt{x^3}}$$

En este caso, tenemos una función trigonométrica. Podemos derivar al recordar que la derivada de seno es igual a coseno y la derivada de coseno es igual a menos seno:

$latex f(x)=\sin(x)-\cos(x)$

$latex f'(x)=\cos(x)+\sin(x)$

Aplicamos las mismas reglas para derivar otra vez:

$latex f'(x)=\cos(x)+\sin(x)$

$latex f^{\prime \prime}(x)=-\sin(x)+\cos(x)$

Podemos empezar simplificando de la siguiente forma:

$$f(x)=\frac{1}{\sqrt{x}}+3x^{-3}+5$$

$latex f(x)=x^{-\frac{1}{2}}+3x^{-3}+5$

Ahora, derivamos usando la regla de la potencia en cada término de la función:

$latex f(x)=x^{-\frac{1}{2}}+3x^{-3}+5$

$$f'(x)=-\frac{1}{2}x^{-\frac{3}{2}}-9x^{-4}$$

Derivamos a $latex f'(x)$ para obtener la segunda derivada:

$$f'(x)=-\frac{1}{2}x^{-\frac{3}{2}}-9x^{-4}$$

$$ f»(x)=\frac{3}{4}x^{-\frac{5}{2}}+36x^{-5}$$

Usamos las leyes de los exponentes nuevamente para simplificar:

$$ f^{\prime \prime}(x)=\frac{3}{4}x^{-\frac{5}{2}}+36x^{-5}$$

$$ f^{\prime \prime}(x)=\frac{3}{4x^{\frac{5}{2}}}+\frac{36}{x^5}$$

$$ f^{\prime \prime}(x)=\frac{3}{4\sqrt{x^5}}+\frac{36}{x^5}$$

Usamos las leyes de los exponentes para escribir así:

$$f(x)=\frac{2}{3x^2}-\frac{4}{x^5}$$

$$ f(x)=\frac{2}{3}x^{-2}-4x^{-5}$$

Usando la regla de la potencia en ambos términos de la función, tenemos:

$$f(x)=\frac{2}{3}x^{-2}-4x^{-5}$$

$$f'(x)=-\frac{4}{3}x^{-3}+20x^{-6}$$

Derivando a $latex f'(x)$, tenemos:

$$f'(x)=-\frac{4}{3}x^{-3}+20x^{-6}$$

$$f^{\prime \prime}(x)=4x^{-4}-120x^{-7}$$

Finalmente, podemos escribir de la siguiente forma:

$$f^{\prime \prime}(x)= \frac{4}{x^4}-\frac{120}{x^7}$$

Para resolver este ejercicio, tenemos que empezar encontrando la primera y la segunda derivada de la función. Entonces, tenemos:

$latex f(x)=4x^3$

$latex f'(x)=12x^2$

$latex f^{\prime \prime}(x)=24x$

Ahora, podemos sustituir en el lado izquierdo de $latex 3f(x)f^{\prime \prime}(x)-2f'(x)^2=0$ y tenemos:

$latex 3f(x)f^{\prime \prime}(x)-2f'(x)^2=0$

$$3(4x^3)(24x)-2(12x^2)^2=0$$

$latex 288x^4-288x^4=0$

Vemos que el lado izquierdo es igual a 0, por lo que hemos demostrado lo requerido.

Similar al ejercicio anterior, tenemos que empezar encontrando la primera y la segunda derivada de la función. Entonces, tenemos:

$$f(x)=\frac{1}{\sqrt{x}}=x^{-\frac{1}{2}}$$

$$f'(x)=-\frac{1}{2}x^{-\frac{3}{2}}$$

$$f^{\prime \prime}(x)=\frac{3}{4}x^{-\frac{5}{2}}$$

Ahora que tenemos las derivadas, vamos a sustituir en el lado izquierdo de $latex 2xf^{\prime \prime}(x)+3f'(x)=0$ y tenemos:

$latex 2xf^{\prime \prime}(x)+3f'(x)=0$

$$2x(\frac{3}{4}x^{-\frac{5}{2}})+3(-\frac{1}{2}x^{-\frac{3}{2}})=0$$

$$\frac{3}{2}x^{-\frac{3}{2}}-\frac{3}{2}x^{-\frac{3}{2}}=0$$

El lado izquierdo es igual a 0, por lo que hemos demostrado que la expresión dada es verdadera.

Las derivadas de la función dada son las siguientes:

$latex f(x)=x^4$

$latex f'(x)=4x^3$

$latex f^{\prime \prime}(x)=12x^2$

Ahora, podemos sustituir en el lado izquierdo de $latex \frac{4y}{3}f^{\prime \prime}(x)-(f'(x))^2=0$ y tenemos:

$$\frac{4y}{3}f^{\prime \prime}(x)-(f'(x))^2=0$$

$$\frac{4(x^4)}{3}(12x^2)-(4x^3)^2=0$$

$latex 16x^6-16x^6=0$

Vemos que el lado izquierdo es igual a 0, por lo que hemos demostrado que la expresión dada es verdadera.