La derivada de la función coseno inversa es igual a menos 1 sobre la raíz cuadrada de 1 menos x al cuadrado, -1/(√(1-x2)). Esta derivada se puede demostrar usando el teorema de Pitágoras y el álgebra.
En este artículo, conoceremos cómo derivar la función coseno inverso. Cubriremos breves fundamentos, una demostración, una comparación gráfica de la función no derivada y derivada, y algunos ejemplos.
CÁLCULO
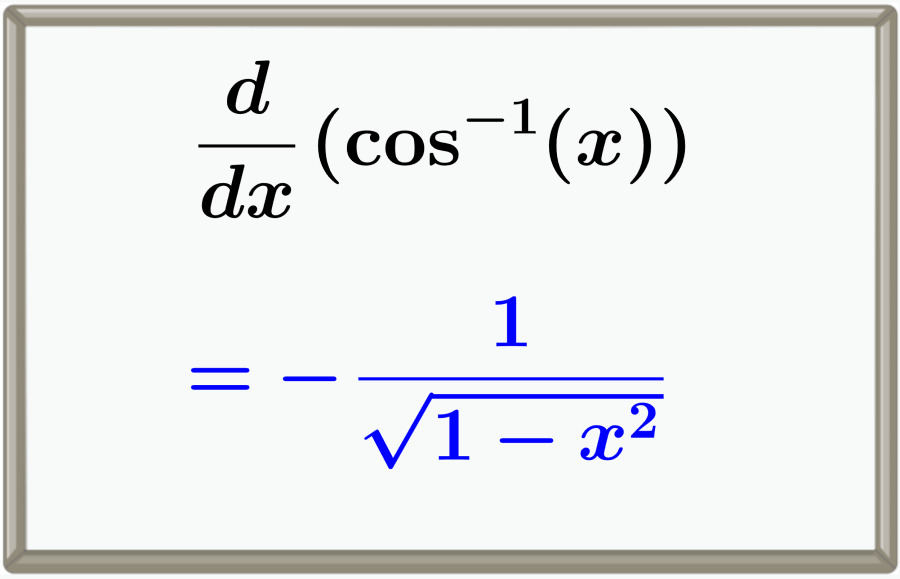
Relevante para…
Aprender sobre la demostración y gráficas de la derivada de arccos de x.
CÁLCULO
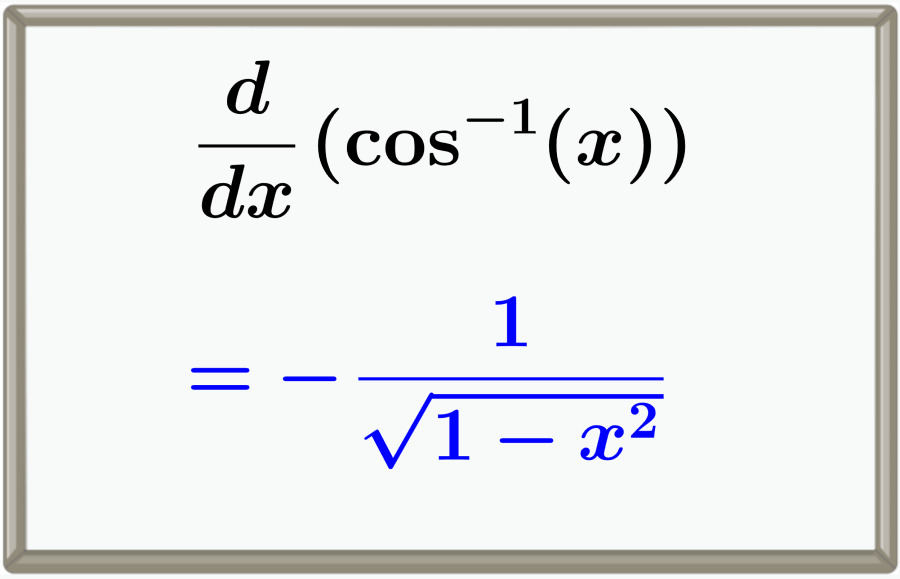
Relevante para…
Aprender sobre la demostración y gráficas de la derivada de arccos de x.
Evite confusiones en el uso de arccos(x), cos-1(x), 1 / cos(x) , y cosn(x)
Es importante evitar posibles confusiones con el uso de las diferentes denotaciones $latex \arccos{(x)}$, $latex \cos^{-1}{(x)}$, $latex \frac {1}{\cos{(x)}}$ y $latex \cos^{n}{(x)}$ porque podría llevar a errores de derivación. Resumiendo la definición de estos símbolos, tenemos
$latex \arccos{(x)} = \cos^{-1}{(x)}$
Los símbolos $latex \arccos$ y $latex \cos^{-1}$ son usados para representar al coseno inverso. $latex \arccos$ se usa comúnmente como el símbolo verbal de la función de coseno inverso, mientras que $latex \cos^{-1}$ se usa como un símbolo matemático de la función de coseno inverso para una función más formal.
Sin embargo, en el caso de la denotación $latex \cos^{-1}{(x)}$, debemos considerar que $latex -1$ no es un exponente algebraico de un coseno no inverso. El $latex -1$ usado para el coseno inverso representa que el coseno es inverso y no elevado a $latex -1$.
Entonces,
$latex \cos^{-1}{(x)} \neq \frac{1}{\cos{(x)}}$
Y $latex \cos^{2}{(x)}$ o $latex \cos^{n}{(x)}$, donde n es cualquier exponente algebraico de un coseno no inverso, NO DEBEN usarse la fórmula del coseno inverso ya que en estos datos, tanto el 2 como cualquier exponente n se tratan como exponentes algebraicos de un coseno no inverso.
Demostración de la derivada de la función coseno inversa
En esta demostración, usaremos principalmente los conceptos de un triángulo rectángulo, el teorema de Pitágoras, la función trigonométrica de coseno y seno y algo de álgebra básica. Supongamos que tenemos un triángulo $latex \Delta ABC$,
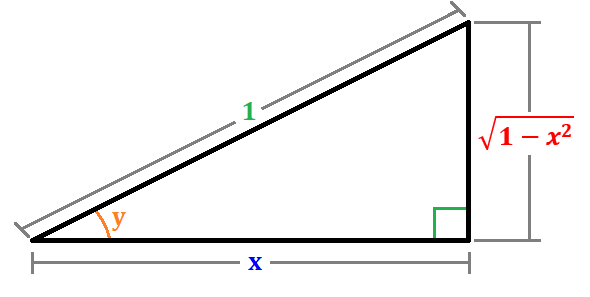
donde por cada unidad de hipotenusa, hay un lado x perpendicular al lado $latex \sqrt{1-x^2}$ y un ángulo y adyacente al lado x y opuesto a $latex \sqrt{1-x^2}$
Usando estos componentes de un triángulo rectángulo, podemos encontrar el ángulo y usando Soh-Cah-Toa, particularmente la función coseno usando su lado adyacente x y la hipotenusa 1.
$latex \cos{(\theta)} = \frac{ady}{hip}$
$latex \cos{(y)} = \frac{x}{1}$
$latex cos{(y)} = x$
Ahora, podemos derivar implícitamente esta ecuación usando la derivada de la función trigonométrica del coseno para el lado izquierdo y la regla de la potencia para el lado derecho. Al hacerlo, tenemos
$latex \frac{d}{dx} (\cos{(y)}) = \frac{d}{dx} (x)$
$latex \frac{d}{dx} (\cos{(y)}) = 1$
$latex \frac{dy}{dx} (-\sin{(y)}) = 1$
$latex \frac{dy}{dx} = \frac{1}{-sin{(y)}}$
$latex \frac{dy}{dx} = -\frac{1}{sin{(y)}}$
Obteniendo el seno de nuestro triángulo rectángulo dado, tenemos
$latex \sin{(y)} = \frac{opu}{hip}$
$latex \sin{(y)} = \frac{\sqrt{1-x^2}}{1}$
$latex \sin{(y)} = \sqrt{1-x^2}$
Entonces podemos sustituir $latex \sin{(y)}$ a la diferenciación implícita de $latex \cos{(y)} = x$
$latex \frac{dy}{dx} = -\frac{1}{sin{(y)}}$
$latex \frac{dy}{dx} = -\frac{1}{\sqrt{1-x^2}}$
Por lo tanto, despejando algebraicamente el ángulo y y obteniendo su derivada, tenemos
$latex \cos{(y)} = x$
$latex y = \frac{x}{\cos}$
$latex y = \cos^{-1}{(x)}$
$latex \frac{dy}{dx} = \frac{d}{dx} \left( \cos^{-1}{(x)} \right)$
$latex \frac{dy}{dx} = -\frac{1}{\sqrt{1-x^2}}$
que ahora es la fórmula de la derivada del coseno inverso de x.
Ahora, para la derivada de un coseno inverso de cualquier función que no sea x, podemos aplicar la fórmula de la derivada del coseno inverso junto con la fórmula de la regla de la cadena. Al hacerlo, tenemos
$latex \frac{dy}{dx} = \frac{d}{du} \cos^{-1}{(u)} \cdot \frac{d}{dx} (u)$
$latex \frac{dy}{dx} = -\frac{1}{\sqrt{1-u^2}} \cdot \frac{d}{dx} (u)$
donde $latex u$ es cualquier función distinta de x.
Gráfica de coseno inverso de x vs. la derivada del coseno inverso de x
La gráfica de la función
$latex f(x) = \cos^{-1}{(x)}$
es
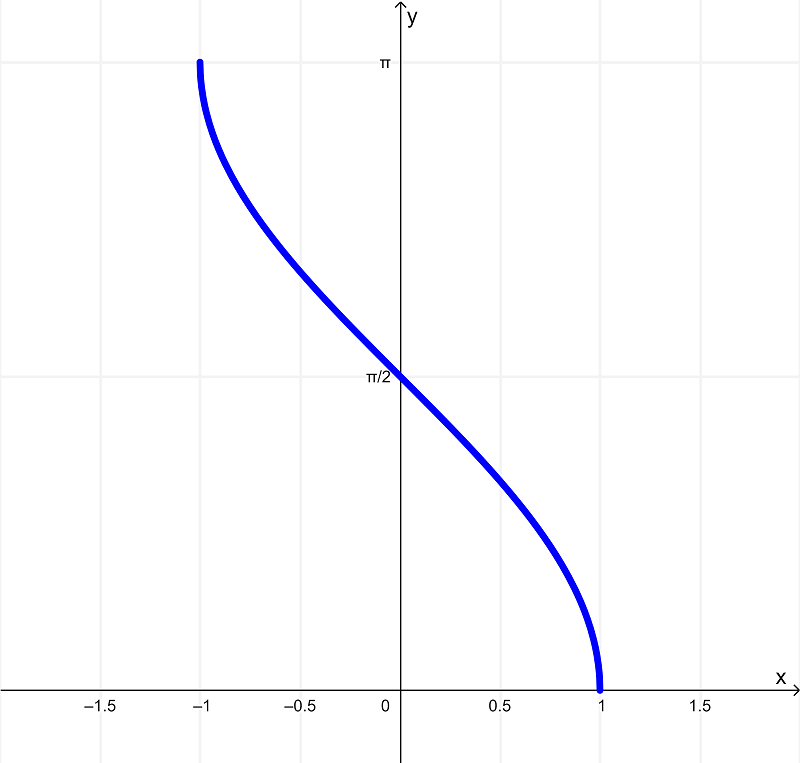
Y al derivar la función $latex f(x) = \cos^{-1}{(x)}$, obtenemos
$latex f'(x) = -\frac{1}{\sqrt{1-x^2}}$
la cual tiene la siguiente gráfica
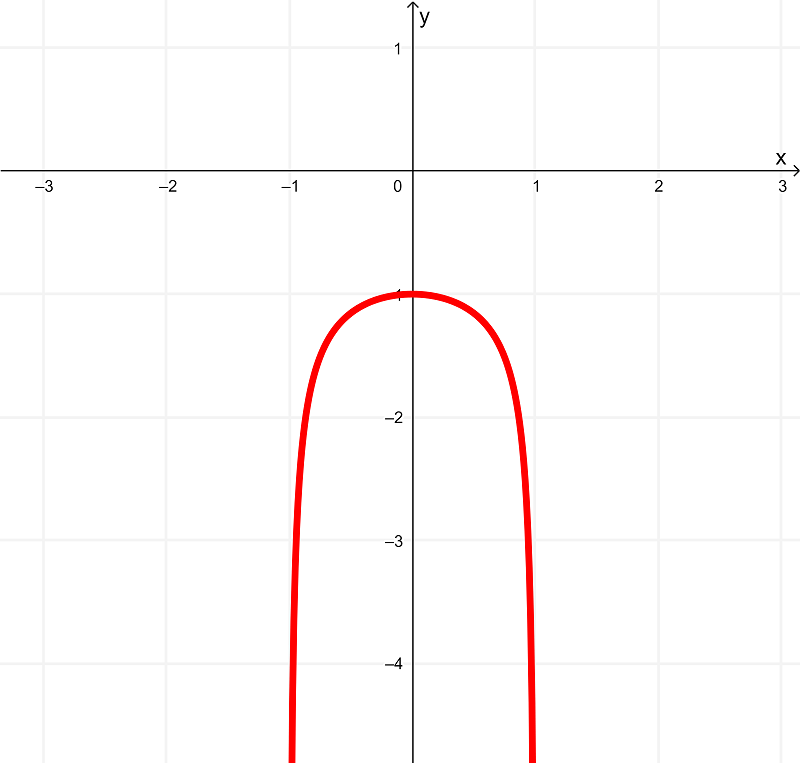
Comparando sus gráficas, tenemos
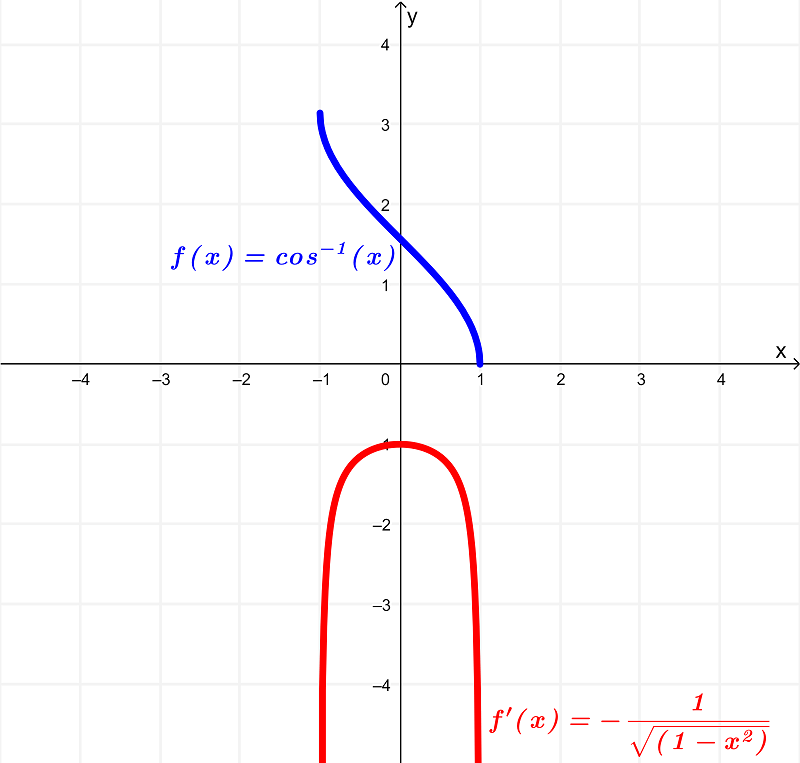
Usando sus gráficas, podemos observar que la función original $latex f(x) = \cos^{-1}{(x)}$ tiene un dominio de
$latex [-1,1]$ o $latex -1 \leq x \leq 1$
y existe dentro del rango de
$latex [0,\pi]$ o $latex 0 \leq y \leq \pi$
mientras que la derivada $latex f'(x) = -\frac{1}{\sqrt{1-x^2}}$ tiene un dominio de
$latex (-1,1)$ o $latex -1 < x < 1$
y existe dentro del rango de
$latex (-\infty,-1]$ o $latex y \leq -1$
Ejemplos
Los siguientes ejemplos muestran cómo derivar funciones coseno inverso compuestas.
EJEMPLO 1
¿Cuál es la derivada de $latex f(x) = \cos^{-1}(8x)$?
Solución
Tenemos una función coseno inverso compuesta. Entonces, tenemos que usar la regla de la cadena para derivarla.
Considerando que $latex u=8x$ es la función interna, tenemos $latex f(u)=\cos^{-1}(u)$. Entonces, al aplicar la regla de la cadena, tenemos:
$$\frac{dy}{dx}=\frac{dy}{du} \frac{du}{dx}$$
$$\frac{dy}{dx}=-\frac{1}{\sqrt{1-u^2}} \times 8$$
Por último, sustituimos $latex u=8x$ de vuelta en la función y tenemos:
$$\frac{dy}{dx}=-\frac{8}{\sqrt{1-(8x)^2}}$$
$$\frac{dy}{dx}=-\frac{8}{\sqrt{1-64x^2}}$$
EJEMPLO 2
Encuentra la derivada de la función $latex F(x) = \cos^{-1}(x^2+10)$
Solución
Vamos a usar la regla de la cadena al escribir a la función coseno inversa como $latex f (u) = \cos^{-1}(u)$, donde $latex u = x^2+10$.
Entonces, empezamos escribiendo la derivada de la función externa $latex f(u)$:
$$\frac{d}{du} ( \cos^{-1}(u) ) = -\frac{1}{\sqrt{1-u^2}}$$
Ahora, calculamos la derivada de la función interna $latex g(x)=u=x^2+10$:
$$\frac{d}{dx}(g(x)) = \frac{d}{dx}(x^2+5)$$
$$\frac{d}{dx}(g(x)) = 2x$$
Luego, multiplicamos a la derivada de la función externa por la derivada de la función interna y tenemos:
$$\frac{dy}{dx} = \frac{d}{du} (f(u)) \cdot \frac{d}{dx} (g(x))$$
$$\frac{dy}{dx} = -\frac{1}{\sqrt{1-u^2}} \cdot 2x$$
Por último, substituimos $latex u$ de vuelta y simplificamos:
$$\frac{dy}{dx} = -\frac{1}{\sqrt{1-(x^2+10)^2}} \cdot 2x$$
$$\frac{dy}{dx} = -\frac{2x}{\sqrt{1-(x^4+20x^2+100)}}$$
$$\frac{dy}{dx} = -\frac{2x}{\sqrt{-x^4-20x^2-99)}}$$
EJEMPLO 3
Encuentra la derivada de $latex f(x) = \cos^{-1}(\sqrt{x})$
Solución
En este caso, la función raíz cuadrada es la función interna. Podemos derivarla al escribir a $latex u=\sqrt{x}$ como $latex u=x^{\frac{1}{2}}$:
$$\frac{du}{dx}=\frac{1}{2}x^{-\frac{1}{2}}$$
Ahora, considerando que $latex f(u)=\cos^{-1}(u)$, aplicamos la regla de la cadena:
$$\frac{dy}{dx}=\frac{dy}{du} \frac{du}{dx}$$
$$\frac{dy}{dx}=-\frac{1}{\sqrt{1-u^2}} \times \frac{1}{2}x^{-\frac{1}{2}}$$
Sustituyendo $latex u=\sqrt{x}$ y simplificando, tenemos:
$$\frac{dy}{dx}=-\frac{1}{\sqrt{1-(\sqrt{x})^2}} \times \frac{1}{2}x^{-\frac{1}{2}}$$
$$\frac{dy}{dx}=-\frac{1}{\sqrt{1-x}} \times \frac{1}{2}x^{-\frac{1}{2}}$$
$$\frac{dy}{dx}=-\frac{1}{2\sqrt{x}\sqrt{1-x}}$$
$$\frac{dy}{dx}=-\frac{1}{2\sqrt{x(1-x)}}$$
Práctica de derivadas de funciones coseno inverso compuestas
Véase también
¿Interesado en aprender más sobre derivadas de funciones trigonométricas inversas? Mira estas páginas:
- Derivada de arco tan (tangente inversa) – Demostración y Gráficas
- Derivada de arco sin (seno inverso) – Demostración y Gráficas
- Derivada de arco sec (secante inversa) – Demostración y Gráficas
- Derivada de arco csc (cosecante inversa) – Demostración y Gráficas
- Derivada de arco cot (cotangente inversa) – Demostración y Gráficas
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
