El área superficial de un prisma rectangular es igual a la superficie total ocupada por el prisma. El área superficial es una medida bidimensional, por lo que puede ser medida en m², cm², entre otros. Para calcular el área superficial, tenemos que sumar las áreas individuales de todas las caras del prisma rectangular. En total tenemos 6 caras en un prisma rectangular, por lo que sumamos las áreas de las seis caras. El área de cada cara depende de dos de las tres dimensiones del prisma, longitud, base y altura.
A continuación, conoceremos la fórmula que podemos usar para encontrar el área superficial de prismas rectangulares. Además, resolveremos algunos ejercicios, en los que aplicaremos esta fórmula.
GEOMETRÍA
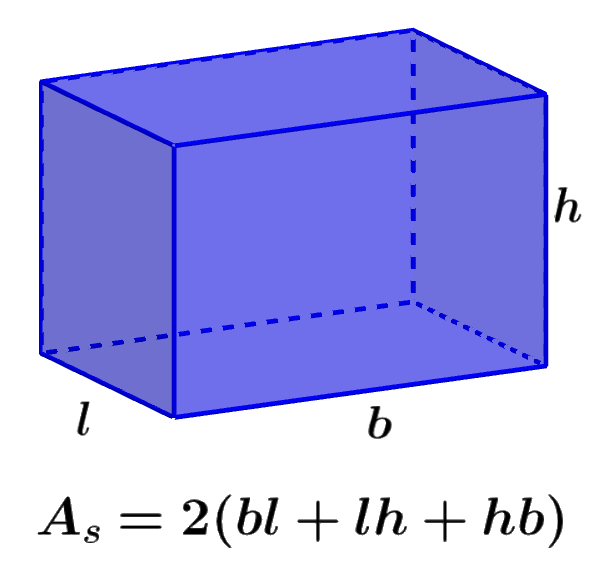
Relevante para…
Aprender a calcular el área superficial de un prisma rectangular.
GEOMETRÍA
Relevante para…
Aprender a calcular el área superficial de un prisma rectangular.
Fórmula del área superficial de un prisma rectangular
Un prisma rectangular tiene dos bases rectangulares paralelas y cuatro caras rectangulares. El área superficial del prisma rectangular es la suma del área de las caras laterales y las bases rectangulares. La unidad de medida del área superficial del prisma rectangular es realizada en unidades cuadradas.
Consideremos al siguiente prisma rectangular con sus dimensiones:
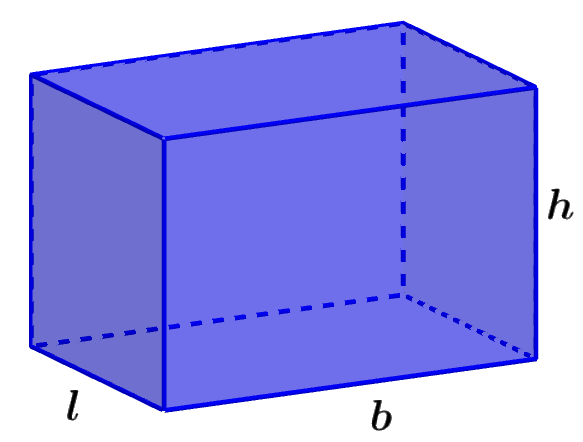
La fórmula del área superficial de este prisma rectangular es:
| $latex A_{S}=2(bl+lh+hb)$ |
en donde,
- b es la longitud de la base del prisma
- l es la longitud del ancho del prisma
- h es la longitud de la altura del prisma
Esta fórmula es derivada al considerar que las caras paralelas en un prisma rectangular tienen la misma área.
Ejercicios de área superficial de prismas rectangulares resueltos
La fórmula del área superficial de prismas rectangulares es aplicada para resolver los siguientes ejercicios. Cada ejercicio tiene su respectiva solución, pero es recomendable que intentes resolver los ejercicios tú mismo.
EJERCICIO 1
Un prisma rectangular tiene una base de 5 m, un ancho de 4 m y una altura de 4 m. ¿Cuál es su área superficial?
Solución
Podemos obtener la siguiente información:
- Base, $latex b=5$
- Ancho, $latex l=4$
- Altura, $latex h=4$
Usamos la fórmula del área superficial con estos valores. Entonces, tenemos:
$latex A_{S}=2(bl+lh+hb)$
$latex A_{S}=2((5)(4)+(4)(4)+(4)(5))$
$latex A_{S}=2(20+16+20)$
$latex A_{S}=2(56)$
$latex A_{S}=112$
El área superficial es 112 m².
EJERCICIO 2
¿Cuál es el área superficial de un prisma rectangular que tiene una base de 7 m, un ancho de 6 m y una altura de 8 m?
Solución
De la pregunta, tenemos los siguientes valores:
- Base, $latex b=7$
- Ancho, $latex l=6$
- Altura, $latex h=8$
Reemplazamos a estos valores en la fórmula del área superficial:
$latex A_{S}=2(bl+lh+hb)$
$latex A_{S}=2((7)(6)+(6)(8)+(8)(7))$
$latex A_{S}=2(42+48+56)$
$latex A_{S}=2(146)$
$latex A_{S}=292$
El área superficial es 292 m².
EJERCICIO 3
Si es que un prisma rectangular tiene una base de 8 m, una altura de 12 m y un ancho de 11 m. ¿Cuál es su área superficial?
Solución
Tenemos la siguiente información:
- Base, $latex b=8$
- Ancho, $latex l=11$
- Altura, $latex h=12$
Al usar estos valores en la fórmula del área superficial, tenemos:
$latex A_{S}=2(bl+lh+hb)$
$$A_{S}=2((8)(11)+(11)(12)+(12)(8))$$
$latex A_{S}=2(88+132+96)$
$latex A_{S}=2(316)$
$latex A_{S}=632$
El área superficial es 632 m².
EJERCICIO 4
¿Cuál es la longitud de la altura de un prisma rectangular que tiene un área superficial de 148 m² si es que su base mide 6 m y su ancho mide 4 m?
Solución
Tenemos la siguiente información:
- Base, $latex b=6$
- Ancho, $latex l=4$
- Área superficial, $latex A=148$
Aquí, tenemos el área superficial y queremos encontrar la longitud de la altura. Entonces, usamos la fórmula y resolvemos para h:
$latex A_{S}=2(bl+lh+hb)$
$latex 148=2((6)(4)+(4)h+(6)(h))$
$latex 148=2(24+10h)$
$latex 74=24+10h)$
$latex 10h=74-24$
$latex 10h=50$
$latex h=5$
La longitud de la altura es 5 m.
EJERCICIO 5
¿Cuál es la longitud de la altura de un prisma rectangular que tiene un área superficial de 340 m², un ancho de 5 m y una base de 8 m?
Solución
Tenemos los siguientes datos:
- Base, $latex b=8$
- Ancho, $latex l=5$
- Área superficial, $latex A=340$
Usamos la fórmula del área superficial con estos datos y resolvemos para h:
$latex A_{S}=2(bl+lh+hb)$
$latex 340=2((8)(5)+(5)h+(8)(h))$
$latex 340=2(40+13h)$
$latex 170=40+13h)$
$latex 13h=170-40$
$latex 13h=130$
$latex h=10$
La longitud de la altura es 10 m.
Ejercicios de área superficial de prismas rectangulares para resolver
Los siguientes ejercicios pueden ser usados para practicar el uso de la fórmula del área superficial de prismas regulares. Si necesitas ayuda con estos ejercicios, puedes mirar los ejercicios resueltos de arriba.
Véase también
¿Interesado en aprender más prismas rectangulares? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
