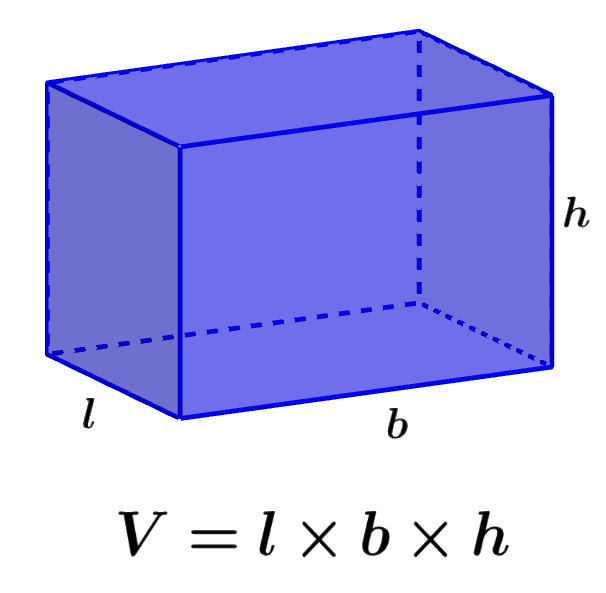
El volumen de un prisma rectangular es la medida del espacio ocupado por el prisma. Un prisma rectangular es un objeto tridimensional con seis caras rectangulares. Un prisma rectangular también es conocido como un cuboide, un hexaedro rectangular o un paralelepípedo rectangular. Para encontrar el volumen de un prisma rectangular, multiplicamos las dimensiones de la longitud, el ancho y la altura.
A continuación, conoceremos la fórmula usada para calcular el volumen de estas figuras geométricas. Además, resolveremos algunos ejercicios en los que aplicaremos esta fórmula para obtener la respuesta.
Fórmula del volumen de un prisma rectangular
La fórmula del volumen de un prisma rectangular es obtenida al multiplicar a la longitud, al ancho y a la altura del prisma. Recordemos que un prisma rectangular tiene dos bases rectangulares paralelas y cuatro caras rectangulares. Todos los ángulos en estos prismas son ángulos rectos.
La fórmula del volumen de un prisma rectangular es:
| $latex V=l\times b \times h$ |
en donde,
- l es la longitud del ancho del prisma
- b es la longitud de la base del prisma
- h es la longitud de la altura del prisma
Ejercicios de volumen de prismas rectangulares resueltos
La fórmula del volumen de prismas rectangulares es usada para resolver los siguientes ejercicios. Intenta resolver los ejercicios tú mismo antes de mirar la solución.
EJERCICIO 1
Un prisma rectangular tiene una base de 5 m, un ancho de 4 m y una altura de 4 m. ¿Cuál es su volumen?
Solución
Tenemos las dimensiones:
- Base, $latex b=5$
- Ancho, $latex l=4$
- Altura, $latex h=4$
Usando la fórmula del volumen con estos valores, tenemos:
$latex V=b \times l \times h$
$latex V=5 \times 4 \times 4$
$latex V=80$
El volumen es igual a 80 m³.
EJERCICIO 2
Si es que un prisma tiene una base de 8 m, un ancho de 6 m y una altura de 7 m, ¿cuál es su volumen?
Solución
Tenemos los siguientes valores:
- Base, $latex b=8$
- Ancho, $latex l=6$
- Altura, $latex h=7$
Reemplazando a estos valores en la fórmula del volumen, tenemos:
$latex V=b \times l \times h$
$latex V=8 \times 6 \times 7$
$latex V=336$
El volumen es igual a 336 m³.
EJERCICIO 3
Un prisma rectangular tiene una base de 10 m, un ancho de 11 m y una altura de 12 m. ¿Cuál es su volumen?
Solución
Reconocemos los siguientes valores:
- Base, $latex b=10$
- Ancho, $latex l=11$
- Altura, $latex h=12$
Al usar estos valores en la fórmula, tenemos:
$latex V=b \times l \times h$
$latex V=10 \times 11 \times 12$
$latex V=1320$
El volumen es igual a 1320 m³.
EJERCICIO 4
¿Cuál es la longitud de la altura de un prisma que tiene una base de 5 m, un ancho de 3 m y un volumen de 90 m³?
Solución
Tenemos los valores:
- Base, $latex b=5$
- Ancho, $latex l=3$
- Volumen, $latex V=90$
En este caso, tenemos el volumen y queremos encontrar la longitud de la altura. Entonces, tenemos que usar la fórmula del volumen y resolver para h:
$latex V=b \times l \times h$
$latex 90=5 \times 3 \times h$
$latex 90=15h$
$latex h=6$
La longitud de la altura es 6 m.
EJERCICIO 5
Un prisma rectangular tiene un volumen de 693 m³, una base de 11 m y un ancho de 9 m. ¿Cuál es su altura?
Solución
Tenemos los valores:
- Base, $latex b=11$
- Ancho, $latex l=9$
- Volumen, $latex V=693$
Usamos la fórmula del volumen y resolvemos para h:
$latex V=b \times l \times h$
$latex 693=11 \times 9 \times h$
$latex 693=99h$
$latex h=7$
La longitud de la altura es 7 m.
Ejercicios de volumen de prismas rectangulares para resolver
Usa la fórmula del volumen de prismas rectangulares para resolver los siguientes ejercicios. Si necesitas ayuda con esto, puedes mirar los ejercicios resueltos de arriba.
Véase también
¿Interesado en aprender más sobre prismas rectangulares? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
