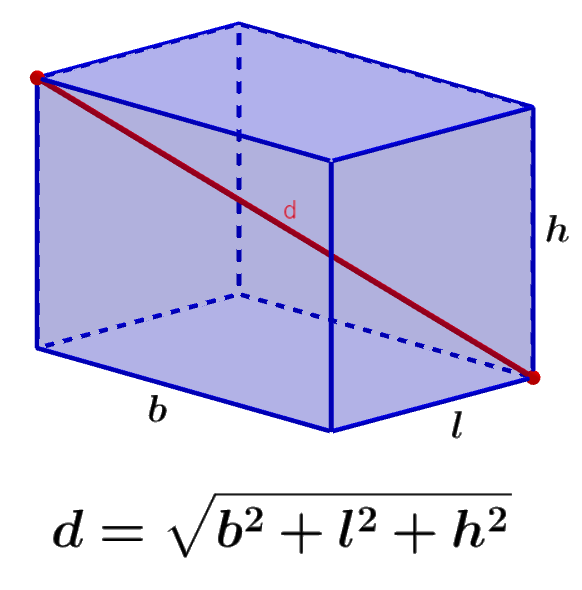
La diagonal de un prisma rectangular es la línea que conecta a un vértice en el prisma con un vértice opuesto. La longitud de la diagonal puede ser calculada usando el teorema de Pitágoras en tres dimensiones. Este teorema es útil cuando tenemos ángulos rectos, tal como tenemos en un prisma rectangular. La fórmula de la diagonal es escrita en términos de la base, del ancho y de la altura del prisma rectangular.
A continuación, conoceremos la fórmula que podemos usar para calcular la diagonal de estos prismas. Además, usaremos esta fórmula para resolver algunos ejercicios de práctica.
Fórmula de la diagonal de un prisma rectangular
La diagonal de un prisma rectangular se extiende desde una esquina del prisma hasta la esquina opuesta del prisma. Podemos usar el teorema de Pitágoras en tres dimensiones para encontrar la longitud de la diagonal usando las longitudes de la base, del ancho y de la altura del prisma.
Entonces, tenemos la fórmula:
| $latex d=\sqrt{{{b}^2}+{{l}^2}+{{h}^2}}$ |
en donde, b es la longitud de la base, l es la longitud del ancho y h es la longitud de la altura.
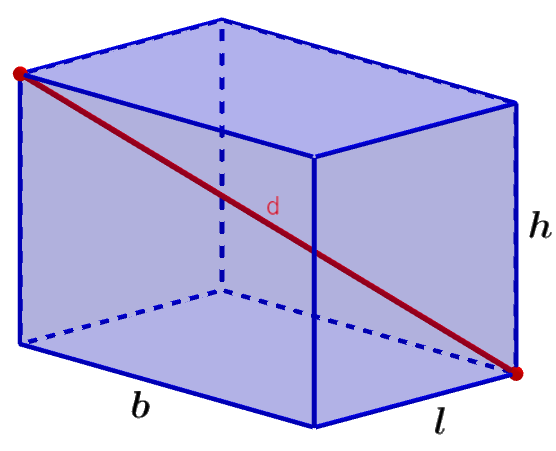
Ejercicios de diagonales de prismas rectangulares resueltos
La fórmula de la diagonal de prismas rectangulares es usada para resolver los siguientes ejercicios. Cada ejercicio tiene su respectiva solución, en donde puedes mirar el razonamiento y proceso usados.
EJERCICIO 1
Un prisma rectangular tiene una base de 5 m, un ancho de 4 m y una altura de 3 m. ¿Cuál es su diagonal?
Solución
Tenemos las siguientes longitudes:
- Base, $latex b=5$
- Ancho, $latex l=4$
- Altura, $latex h=3$
Usando la fórmula de la diagonal con estos valores, tenemos:
$latex d=\sqrt{{{b}^2}+{{l}^2}+{{h}^2}}$
$latex d=\sqrt{{{5}^2}+{{4}^2}+{{3}^2}}$
$latex d=\sqrt{25+16+9}$
$latex d=\sqrt{50}$
$latex d=7.07$
La diagonal mide 7.07 m.
EJERCICIO 2
Si es que un prisma rectangular tiene una base de 6 m, un ancho de 5 m y una altura de 7 m, ¿cuál es su diagonal?
Solución
Tenemos la siguiente información:
- Base, $latex b=6$
- Ancho, $latex l=5$
- Altura, $latex h=7$
Reemplazamos a estos valores en la fórmula de la diagonal:
$latex d=\sqrt{{{b}^2}+{{l}^2}+{{h}^2}}$
$latex d=\sqrt{{{6}^2}+{{5}^2}+{{7}^2}}$
$latex d=\sqrt{36+25+49}$
$latex d=\sqrt{50}$
$latex d=10.49$
La diagonal mide 10.49 m.
EJERCICIO 3
¿Cuál es la longitud de la diagonal de un prisma rectangular que tiene una base de longitud 10 m, un ancho de 5 m y una altura de 6 m?
Solución
Tenemos la siguiente información:
- Base, $latex b=10$
- Ancho, $latex l=5$
- Altura, $latex h=6$
Usando estos valores en la fórmula, tenemos:
$latex d=\sqrt{{{b}^2}+{{l}^2}+{{h}^2}}$
$latex d=\sqrt{{{10}^2}+{{5}^2}+{{6}^2}}$
$latex d=\sqrt{100+25+36}$
$latex d=\sqrt{161}$
$latex d=12.69$
La diagonal mide 12.69 m.
EJERCICIO 4
¿Cuál es la longitud de la diagonal de un prisma rectangular que tiene una base de longitud 12 m, un ancho de 11 m y una altura de 8 m?
Solución
Tenemos los siguientes datos:
- Base, $latex b=12$
- Ancho, $latex l=11$
- Altura, $latex h=8$
Reemplazando estos valores en la fórmula, tenemos:
$latex d=\sqrt{{{b}^2}+{{l}^2}+{{h}^2}}$
$latex d=\sqrt{{{12}^2}+{{11}^2}+{{8}^2}}$
$latex d=\sqrt{144+121+64}$
$latex d=\sqrt{329}$
$latex d=18.14$
La diagonal mide 18.14 m.
Ejercicios de diagonal de prismas rectangulares para resolver
Usa la fórmula de la diagonal de prismas rectangulares para resolver los siguientes ejercicios. Si necesitas ayuda con esto, puedes mirar los ejercicios resueltos de arriba.
Véase también
¿Interesado en aprender más sobre prismas rectangulares? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
