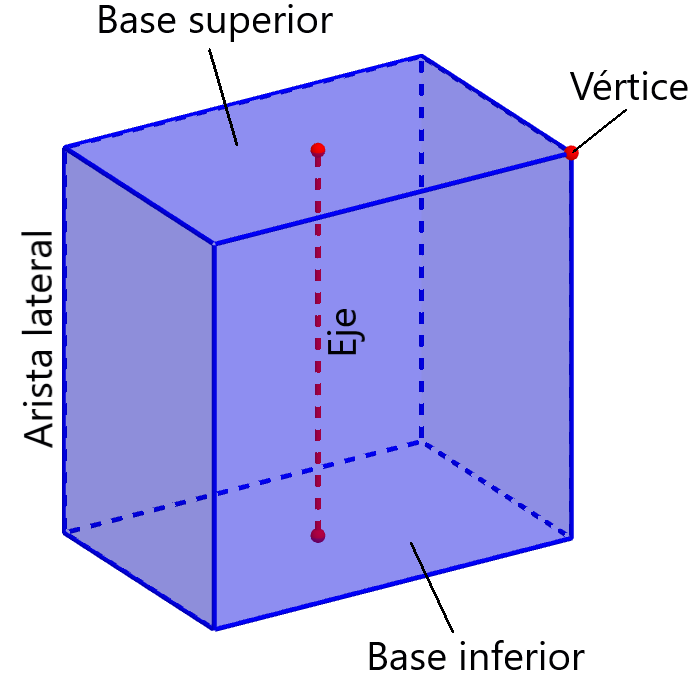
El prisma es un poliedro en el que dos caras son polígonos iguales en planos paralelos y todas las otras cuatro caras son paralelogramos. En el caso de prismas rectangulares, todas las caras tienen una figura de rectángulo. Hay dos tipos principales de estos prismas: prismas rectos y prismas oblicuos. Un prisma oblicuo es cuando la base no es perpendicular al eje y el prisma recto es cuando el eje y la base son perpendiculares. Los más comunes son los prismas rectos.
A continuación, conoceremos los elementos más importantes de un prisma rectangular. También, veremos sus fórmulas más usadas y las aplicaremos para resolver algunos ejercicios de prismas.
Elementos de un prisma rectangular
Los elementos de un prisma rectangular son:
- Base
- Altura
- Eje
- Arista lateral
- Área lateral
- Sección transversal
- Vértice
Base
Un prisma tiene dos bases paralelas iguales, la base superior y la base inferior. El área de la base es denotada por $latex A_{b}$.
Altura
La altura es la distancia perpendicular entre las dos bases. Esta longitud es denotada por h.
Eje
El eje es la línea que conecta al centroide de la base inferior y superior. La longitud del eje es igual a la longitud de la arista lateral.
Arista lateral
Las aristas laterales son las líneas que conectan a los vértices correspondientes de las bases. En general, una arista es la línea formada por la intersección de dos caras. La arista lateral es la línea formada por la intersección de dos caras laterales.
Área lateral
El área lateral es el área de las caras laterales del prisma. Las caras opuestas en un prisma rectangular son iguales, por lo que estos prismas pueden tener dos áreas laterales diferentes.
Sección transversal
La sección transversal es la sección formada al cortar al prisma con un plano que es perpendicular al eje del prisma.
Vértice
El vértice de un prisma rectangular es un punto formado por la intersección de tres aristas.
Fórmulas importantes de un prisma rectangular
Las fórmulas más usadas en los prismas rectangulares son la fórmula del volumen, la fórmula del área superficial y la fórmula de la diagonal.
Fórmula del volumen
El volumen de un prisma rectangular puede ser calculado al multiplicar las longitudes de las tres dimensiones:
| $latex V=b\times l \times h$ |
en donde, b es la longitud de la base, l es la longitud del ancho y h es la longitud de la altura del prisma rectangular.
Fórmula del área superficial
Calculamos el área superficial al sumar las áreas de todas las caras del prisma. Considerando que las caras opuestas tienen la misma área, tenemos:
| $latex A_{s}=2(bl+bh+hl)$ |
Fórmula de la diagonal
La longitud de la diagonal de un prisma rectangular es calculada usando el teorema de Pitágoras en tres dimensiones:
| $latex d=\sqrt{{{b}^2}+{{l}^2}+{{h}^2}}$ |
Ejemplos de problemas con prismas rectangulares
EJEMPLO 1
Si es que un prisma rectangular tiene una base de longitud 6 m, un ancho de 7 m y una altura de 10 m, ¿cuál es su volumen?
Solución: Usamos la fórmula del volumen con la información dada:
$latex V=b\times l \times h$
$latex V=6\times 7 \times 10$
$latex V=420$
El volumen del prisma es 420 m³,
EJEMPLO 2
¿Cuál es el área superficial de un prisma rectangular que tiene una base de 6 m, un ancho de 8 m y una altura de 7 m?
Solución: Usamos la fórmula del área superficial con la información dada:
$latex A_{s}=2(bl+bh+hl)$
$latex A_{s}=2((6)(8)+(6)(7)+(7)(8))$
$latex A_{s}=2(48+42+56)$
$latex A_{s}=2(146)$
$latex A_{s}=292$
El área superficial del prisma es 292 m²,
EJEMPLO 3
¿Cuál es la diagonal de un prisma rectangular que tiene una base de 5 m, un ancho de 4 m y una altura de 3 m?
Solución: Usamos la fórmula de la diagonal con la información dada:
$latex d=\sqrt{{{b}^2}+{{l}^2}+{{h}^2}}$
$latex d=\sqrt{{{5}^2}+{{4}^2}+{{3}^2}}$
$latex d=\sqrt{25+16+9}$
$latex d=\sqrt{50}$
$latex d=7.07$
La diagonal del prisma mide 7.07 m,
Véase también
¿Interesado en aprender más sobre prismas rectangulares? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
