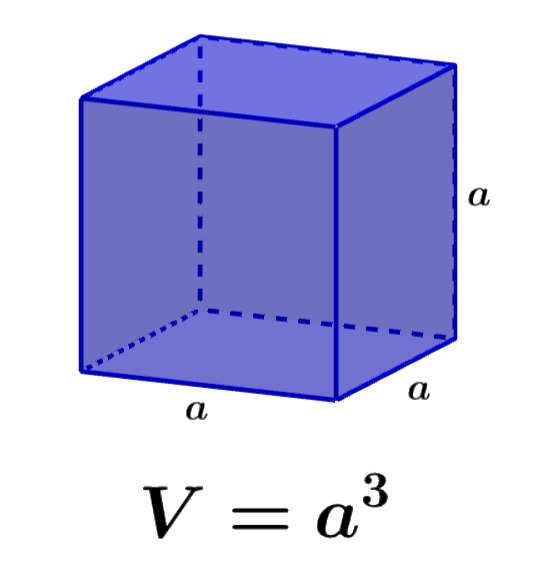
El volumen de un cubo define el número de unidades cúbicas que son ocupadas por el cubo completamente. Un cubo es una figura sólida tridimensional, la cual tiene seis caras cuadradas. Para calcular el volumen, necesitamos conocer la dimensión de sus lados. Debido a que un cubo tiene todos sus lados con la misma longitud, podemos encontrar el volumen del cubo al elevar a uno de sus lados a la potencia de 3.
A continuación, conoceremos la fórmula que podemos usar para encontrar el volumen de cubos. Aprenderemos a derivar esta fórmula y la usaremos para resolver algunos ejercicios.
Fórmula del volumen de un cubo
Fácilmente podemos calcular el volumen de cubos si es que conocemos la longitud de uno de sus lados. El volumen es el producto de la longitud, el ancho y la altura. En el caso de cubos, sabemos que todos sus lados tienen longitudes iguales, por lo que tenemos:
Volumen = Longitud × Ancho × Altura
$latex V=a\times a \times a$
| $latex V={{a}^3}$ |
en donde, a es la longitud de uno de los lados del cubo.
Derivación de la fórmula del volumen
Sabemos que un cubo es un objeto tridimensional que tiene longitud, ancho y altura con la misma longitud. Podemos derivar su fórmula del volumen de la siguiente manera:
- Consideremos una hoja de papel cuadrada.
- El área de esa hoja cuadrada será igual a su longitud multiplicada por su ancho.
- Dado que en un cuadrado la longitud y el ancho son iguales, su área será $latex {{a}^2}$.
- Un cubo es formado al apilar varias hojas de papel una encima de la otra hasta obtener una altura igual a a.
- Podemos concluir que el volumen cubierto por el cubo es igual al área de la base multiplicada por la altura.
- Entonces, el volumen del cubo es igual a $latex {{a}^3}$.
Volumen de un cubo usando la diagonal
También es posible calcular el volumen de un cubo usando la longitud de la diagonal. Para esto, podemos usar la siguiente fórmula:
| $latex V=\sqrt{3} \times \frac{{{d}^3}}{9}$ |
en donde, d es la longitud de la diagonal de un cubo.
Ejercicios de volumen de un cubo resueltos
Los siguientes ejercicios pueden ser usados para practicar la aplicación de las fórmulas del volumen de cubos. Cada ejercicio tiene su respectiva solución, en donde el proceso y razonamiento usados son detallados.
EJERCICIO 1
¿Cuál es el volumen de un cubo que tiene lados de longitud 5 m?
Solución
Podemos usar la primera fórmula del volumen con la longitud $latex a=5$. Entonces, tenemos:
$latex V=a^3$
$latex V={{5}^3}$
$latex V=125$
El volumen es igual a 125 m³.
EJERCICIO 2
Si es que un cubo tiene lados de longitud 10 m, ¿cuál es su volumen?
Solución
Tenemos la longitud $latex a=10$, por lo que reemplazamos este valor en la fórmula del volumen:
$latex V=a^3$
$latex V={{10}^3}$
$latex V=1000$
El volumen es igual a 1000 m³.
EJERCICIO 3
Un cubo tiene un volumen de 512 cm³. ¿Cuál es la longitud de uno de sus lados?
Solución
En este caso, empezamos con el área y queremos encontrar la longitud de uno de los lados. Usamos la fórmula del volumen y resolvemos para a:
$latex V=a^3$
$latex 512={{a}^3}$
$latex a=8$
La longitud de uno de los lados es 8 cm.
EJERCICIO 4
¿Cuál es el volumen de un cubo que tiene una diagonal de 5 m?
Solución
Aquí, tenemos la longitud $latex d=5$, por lo que usamos la segunda fórmula con este valor:
$latex V=\sqrt{3}\times \frac{{{d}^3}}{9}$
$latex V=\sqrt{3}\times \frac{{{5}^3}}{9}$
$latex V=\sqrt{3}\times \frac{125}{9}$
$latex V=24.1$
El volumen es igual a 24.1 m³.
EJERCICIO 5
Un cubo tiene una diagonal de 10 m. ¿Cuál es su volumen?
Solución
Tenemos la longitud $latex d=10$, por lo que usamos la segunda fórmula con este valor:
$latex V=\sqrt{3}\times \frac{{{d}^3}}{9}$
$latex V=\sqrt{3}\times \frac{{{10}^3}}{9}$
$latex V=\sqrt{3}\times \frac{1000}{9}$
$latex V=192.5$
El volumen es igual a 192.5 m³.
Ejercicios de volumen de cubos para resolver
Pon en práctica las fórmulas del volumen de cubos vistas arriba para resolver los siguientes ejercicios. Si necesitas ayuda con esto, puedes mirar los ejercicios resueltos de arriba.
Véase también
¿Interesado en aprender más sobre cubos? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
