El cubo es uno de los objetos sólidos tridimensionales más comunes. La característica principal de los cubos es que tienen todos sus lados con la misma longitud. Los cubos tienen 6 caras, 12 aristas y 8 vértices. Estas figuras tienen ejemplos muy comunes en la vida real, tal como el cubo de Rubik y un dado estándar de 6 lados.
A continuación, veremos una definición más detallada de los cubos y usaremos diagramas para ilustrar los conceptos. También, conoceremos las características más importantes de los cubos. Finalmente, veremos las fórmulas más importantes de estas figuras geométricas y las usaremos para resolver algunos ejercicios.
GEOMETRÍA
Relevante para…
Conocer las características fundamentales de los cubos.
GEOMETRÍA
Relevante para…
Conocer las características fundamentales de los cubos.
Definición de un cubo
El cubo es un objeto sólido tridimensional limitado por seis caras cuadradas. Tres de estas caras se encuentran en cada vértice. El cubo también es definido como un hexaedro, es decir, un sólido con seis caras. Los cubos son un tipo de prismas cuadrados.
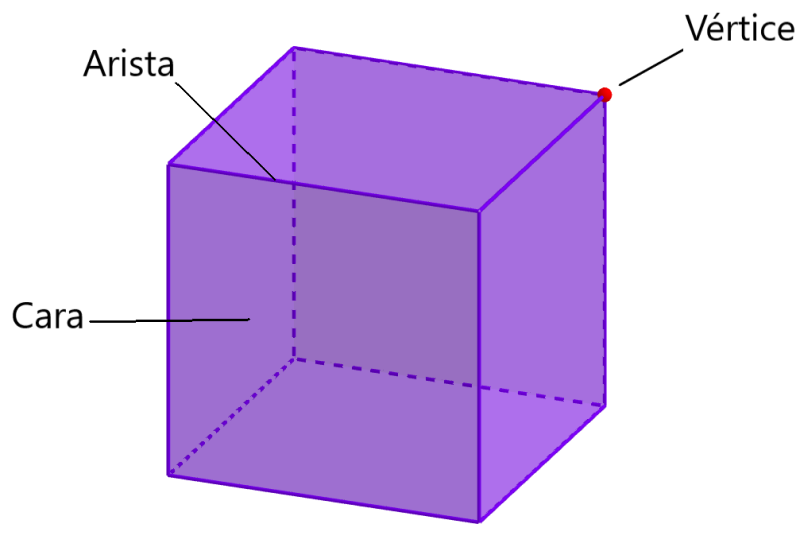
Muchas veces, la figura de un cubo es considerada como un bloque, en donde, la longitud, la altura y el ancho son todos los mismos. Además, una característica principal de los cubos es que tienen 6 caras, 8 vértices y 12 aristas. Podemos distinguir a estos elementos en el siguiente diagrama.
En la imagen, podemos observar al vértice, a la cara y a la arista. Las caras del cubo son conectadas por cuatro vértices. Las aristas del cubo son conectadas en un solo punto, el cual es el vértice. Dado que el cubo es una figura 3D, los dos parámetros importantes usados para medir al cubo son el volumen y el área superficial.
Características principales de un cubo
Las siguientes son las características más importantes de los cubos:
- Todas sus caras tienen una figura cuadrada.
- Todas las caras y los lados tienen dimensiones iguales.
- Cada una de las caras se encuentra con cuatro caras.
- Los ángulos internos del cubo son ángulos rectos.
- Cada uno de los vértices se encuentra con tres caras y tres aristas.
- Las aristas opuestas la una a la otra son paralelas.
Fórmulas importantes de cubos
Las fórmulas más importantes de los cubos para resolver ejercicios son la fórmula del volumen, la fórmula del área superficial y la fórmula de la diagonal.
Fórmula del volumen
El volumen de un cubo puede ser calculado multiplicado las longitudes de sus tres dimensiones. Dado que todos los lados tienen la misma medida, tenemos:
| $latex V={{a}^3}$ |
en donde, a representa a la longitud de uno de los lados.
Fórmula del área superficial
El área superficial es la suma de las áreas de todas las caras del cubo. Sabemos que tenemos seis caras iguales en un cubo y también que el área de una cara es igual al área de un cuadrado, por lo que tenemos:
| $latex A_{s}=6{{a}^2}$ |
en donde, a es la longitud de uno de los lados.
Fórmula de la diagonal
La fórmula de la diagonal de un cubo es derivada al usar el teorema de Pitágoras dos veces. Luego, de simplificar, tenemos la siguiente expresión:
| $latex d=\sqrt{3}~a$ |
en donde, d representa a la longitud de la diagonal y a representa a la longitud de uno de los lados.
Ejercicios de cubos resueltos
Los siguientes ejercicios son resueltos aplicando las fórmulas de cubos vistas arriba.
EJERCICIO 1
¿Cuál es el volumen de un cubo que tiene lados de longitud 8 m?
Solución: Usamos la longitud $latex a=8$ en la fórmula del volumen. Entonces, tenemos:
$latex V={{a}^3}$
$latex V={{8}^3}$
$latex V=512$
El volumen del cubo es 512 m³.
EJERCICIO 2
Un cubo tiene lados de longitud 10 m. ¿Cuál es su área superficial?
Solución: Tenemos la longitud $latex a=10$, por lo que usamos este valor en la fórmula del área superficial:
$latex A_{s}=6{{a}^2}$
$latex A_{s}=6{{(10)}^2}$
$latex A_{s}=6(100)$
$latex A_{s}=600$
El área superficial es 600 m².
EJERCICIO 3
Si un cubo tiene lados de longitud 20 m, ¿cuál es la longitud de su diagonal?
Solución: Usamos la longitud $latex a=20$ en la fórmula de la diagonal. Entonces, tenemos:
$latex d=\sqrt{3}~a$
$latex d=\sqrt{3}(20)$
$latex d=34.64$
La longitud de la diagonal es 34.64 m.
Véase también
¿Interesado en aprender más sobre cubos? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
