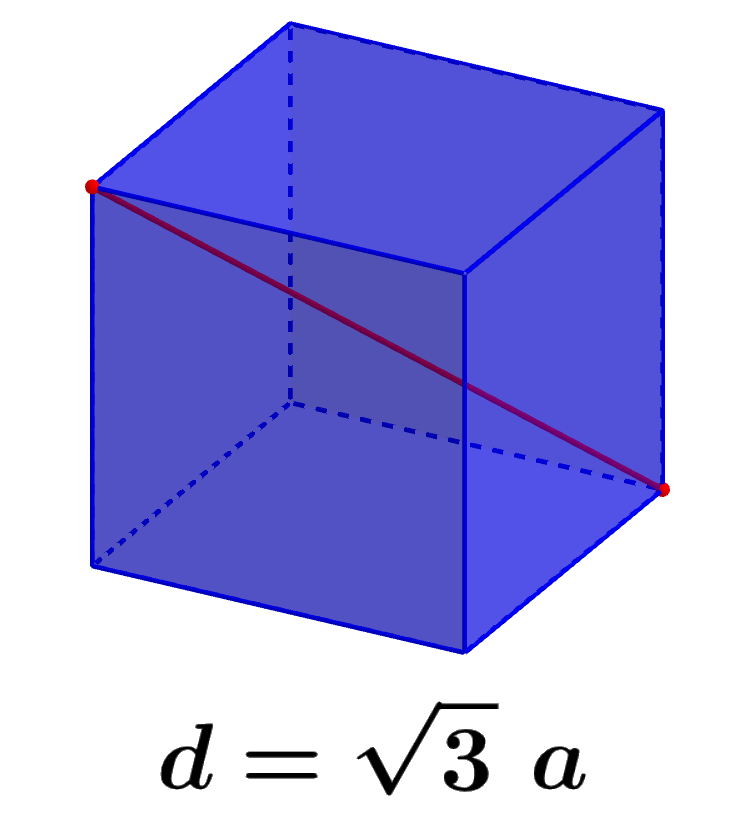
La longitud de la diagonal interna de un cubo puede ser calculada usando el teorema de Pitágoras. A través de dos pasos, podemos encontrar una fórmula para la diagonal de cubos. El primer paso requiere que calculemos la diagonal de una de las caras del cubo usando la longitud de los lados. En el segundo paso, usamos la diagonal de una cara y uno de los lados para encontrar la fórmula final de la diagonal interna de un cubo.
A continuación, veremos estos pasos detalladamente. Derivaremos la fórmula de la diagonal de un cubo y la usaremos para resolver algunos ejercicios.
Fórmula de la diagonal de un cubo
Existen dos diagonales de un cubo, la diagonal interna del cubo y la diagonal de una cara. En la siguiente imagen, podemos ver que ambas son diferentes. La diagonal interna empieza en un vértice y se extiende hasta el vértice opuesto.
La diagonal de una cara empieza en un vértice y termina en otro vértice de modo que se ubica completamente en una sola cara.
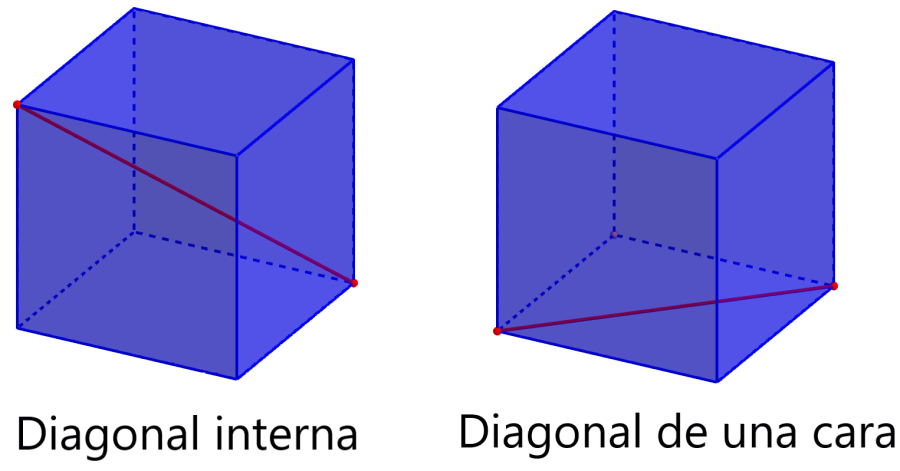
Para calcular la diagonal de una cara del cubo, tenemos que usar el teorema de Pitágoras una vez. Sin embargo, para calcular la diagonal interna, necesitamos usar el teorema de Pitágoras dos veces. Entonces, realizamos esto en dos pasos:
Paso 1: Calculamos la diagonal de una cara. Todas las caras de un cubo son cuadradas, por lo que tenemos lo siguiente:
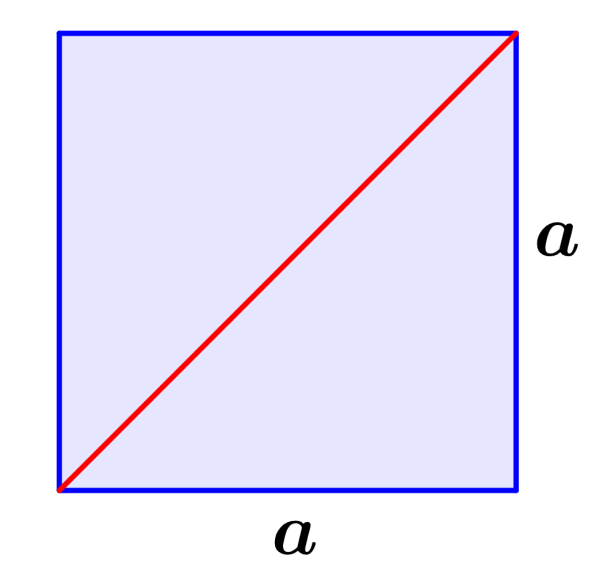
Para encontrar esta distancia, tenemos que usar el teorema de Pitágoras. Si es que usamos la c para representar a la diagonal, tenemos lo siguiente:
$latex {{c}^2}={{a}^2}+{{a}^2}$
$latex {{c}^2}=2{{a}^2}$
$latex c=\sqrt{2{{a}^2}}$
| $latex c=\sqrt{2}~a$ |
Entonces, hemos encontrado una fórmula para la diagonal de la cara.
Paso 2: Para encontrar una expresión para la diagonal interna, tenemos que usar otro triángulo rectángulo. Usamos a la diagonal de una cara como la base del triángulo, a un lado del cubo como la altura del triángulo y a la diagonal interna como la hipotenusa:
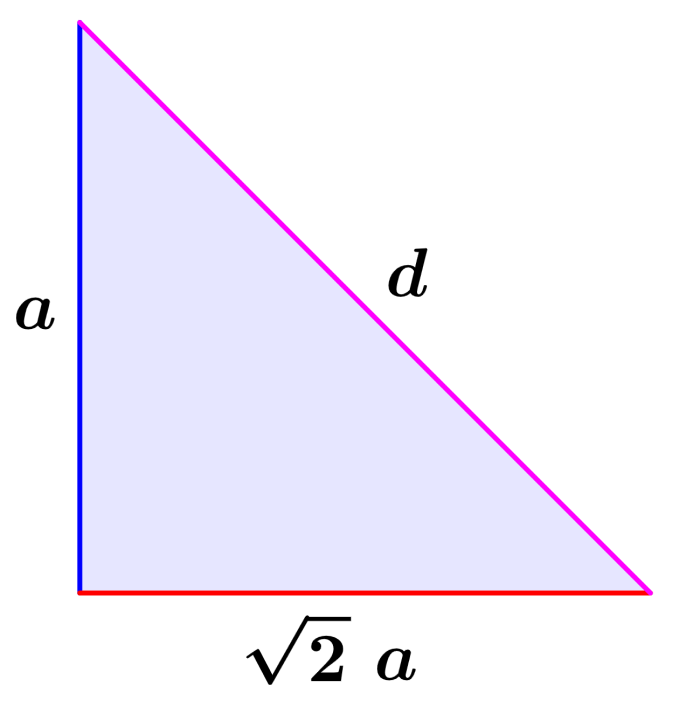
Tenemos que usar el teorema de Pitágoras nuevamente para encontrar la longitud de la diagonal representada por d, por lo que tenemos:
$latex {{d}^2}={{a}^2}+{{(\sqrt{2}~a)}^2}$
$latex {{d}^2}={{a}^2}+2{{a}^2}$
$latex {{d}^2}=3{{a}^2}$
$latex d=\sqrt{3{{a}^2}}$
| $latex d=\sqrt{3}~a$ |
Encontramos la fórmula de la diagonal interna de un cubo.
Ejercicios de diagonales de cubos resueltos
Los siguientes ejercicios de diagonales de cubos pueden ser usados para practicar el uso de la fórmula derivada arriba. Es recomendable que intentes resolver los ejercicios tú mismo antes de mirar la solución.
EJERCICIO 1
¿Cuál es la diagonal de un cubo que tiene lados de longitud 5 m?
Solución
Podemos usar la fórmula de la diagonal con $latex a=5$. Entonces, tenemos:
$latex d=\sqrt{3}~a$
$latex d=\sqrt{3}(5)$
$latex d= 8.66$
La diagonal mide 8.66 m.
EJERCICIO 2
Si es que un cubo tiene lados de longitud de 6 m, ¿cuál es su diagonal?
Solución
Usamos el valor $latex a=6$ en la fórmula de la diagonal. Entonces, tenemos:
$latex d=\sqrt{3}~a$
$latex d=\sqrt{3}(6)$
$latex d= 10.4$
La diagonal tiene una longitud de 10.4 m.
EJERCICIO 3
Un cubo tiene lados de longitud 21 cm. ¿Cuál es su diagonal?
Solución
Tenemos la longitud $latex a=21$, por lo que usamos este valor en la fórmula de la diagonal:
$latex d=\sqrt{3}~a$
$latex d=\sqrt{3}(21)$
$latex d= 36.37$
La diagonal mide 36.37 cm.
EJERCICIO 4
Si es que la diagonal de un cubo mide 10 m, ¿cuál es la longitud de sus lados?
Solución
En este caso, tenemos la longitud de la diagonal y queremos encontrar la longitud de los lados, por lo que usamos $latex d=10$ y resolvemos para a:
$latex d=\sqrt{3}~a$
$latex 10=\sqrt{3}~a$
$latex a= \frac{10}{\sqrt{3}}$
$latex a=5.77$
Los lados tienen una longitud de 5.77 m.
EJERCICIO 5
¿Cuál es la longitud de los lados de un cubo que tiene una diagonal de 20 m?
Solución
Usamos la longitud de la diagonal $latex d=20$ y resolvemos para a:
$latex d=\sqrt{3}~a$
$latex 20=\sqrt{3}~a$
$latex a= \frac{20}{\sqrt{3}}$
$latex a=11.55$
Los lados tienen una longitud de 11.55 m.
Ejercicios de diagonal de cubos para resolver
Pon en práctica el uso de la fórmula de la diagonal de cubos para resolver los siguientes ejercicios. Selecciona una respuesta y verifícala para comprobar que obtuviste la respuesta correcta.
Véase también
¿Interesado en aprender más sobre cubos? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
