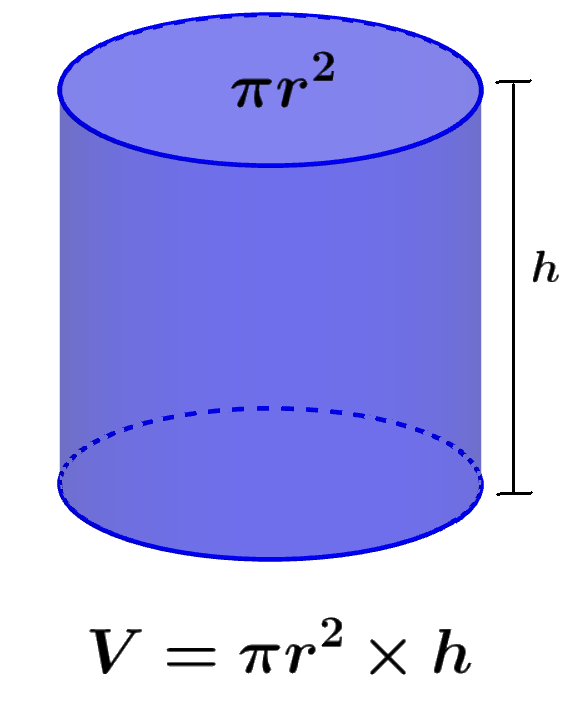
El volumen de un cilindro es la densidad del cilindro, lo que significa la cantidad de material que puede caber en el cilindro o la cantidad de espacio ocupada por el cilindro. Recordemos que el cilindro es una figura tridimensional que tiene bases circulares. Un cilindro puede ser visto como un par de discos circulares que están colocados uno encima del otro. Por lo tanto, calculamos su volumen al multiplicar el área de las bases circulares por la altura del cilindro.
A continuación, conoceremos la fórmula que podemos usar para calcular el volumen de un cilindro tanto en términos del radio y la altura como en términos del diámetro. También, aprenderemos a calcular el volumen de cilindros huecos. Finalmente, usaremos las fórmulas aprendidas para resolver algunos ejercicios.
Fórmula del volumen de un cilindro
Un cilindro puede ser visto como un conjunto de discos congruentes ubicados uno encima del otro. Para calcular el espacio ocupado por el cilindro, calculamos el espacio ocupado por cada disco y luego los sumamos.
Entonces, el volumen de un cilindro está dado por el producto del área de la base y la altura:
Volumen = Base × Altura
Sabemos que un cilindro tiene bases circulares, por lo que el área de la base es igual a πr², en donde r es el radio. Entonces, la fórmula del volumen de un cilindro es:
| $latex V=\pi {{r}^2}\times h$ |
en donde, r es la longitud del radio del cilindro y h es la longitud de su altura.
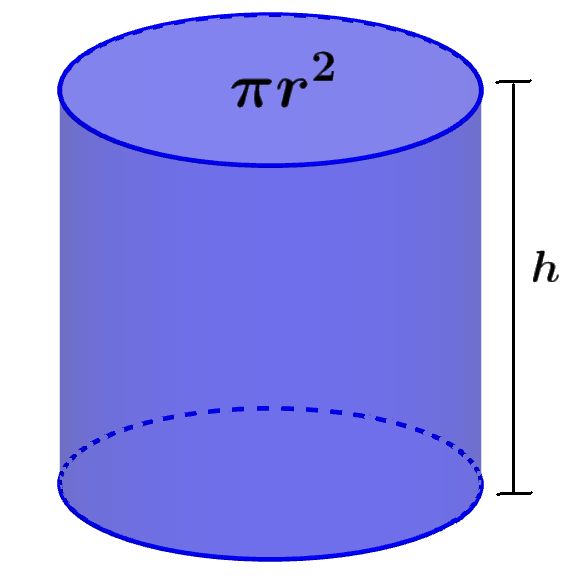
Volumen de un cilindro usando el diámetro
También es posible calcular el volumen de un cilindro usando la longitud de su diámetro. Podemos usar dos métodos para lograr esto.
El primer método consiste en recordar que el diámetro de un cilindro es igual a 2r, en donde r es la longitud del radio del cilindro. Entonces, si es que conocemos el diámetro del cilindro, simplemente podemos dividir el diámetro por 2 para obtener la longitud del radio y aplicar la fórmula del volumen indicada arriba.
Alternativamente, también es posible escribir la equivalencia del radio y el diámetro y obtener una fórmula para el volumen en términos del diámetro del cilindro:
$latex V=\pi {{r}^2}\times h$
$latex V=\pi {{(\frac{d}{2})}^2}\times h$
$latex V=\pi \frac{{{d}^2}}{4}\times h$
| $latex V= \frac{\pi{{d}^2}}{4}\times h$ |
en donde, d es la longitud del diámetro.
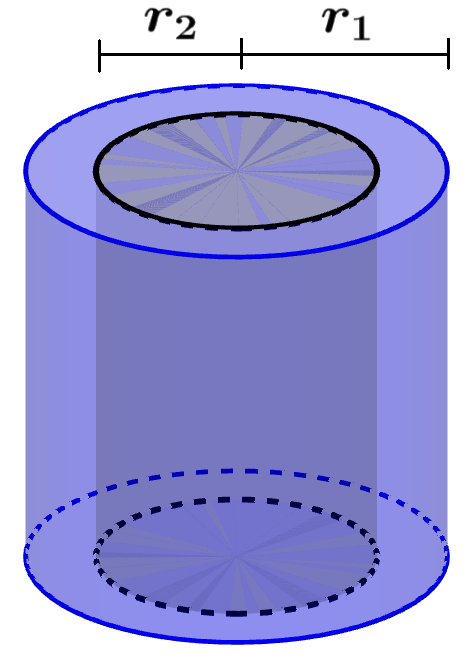
Volumen de un cilindro hueco
En el caso de cilindros huecos, medimos dos radios, uno para el círculo interior y otro para el círculo exterior formados por la base del cilindro hueco. El volumen de este tipo de cilindros puede ser calculado con la siguiente fórmula:
| $latex V=\pi h({{r_{1}}^2}-{{r_{2}}^2})$ |
en donde, $latex r_{1}$ es el radio del círculo exterior, $latex r_{2}$ es el radio del círculo interior y h es la altura del cilindro.
Esta fórmula es equivalente a calcular el volumen de un cilindro entero y luego extraer el volumen del cilindro interno que fue removido.
Ejercicios de volumen de cilindros resueltos
Las fórmulas del volumen de cilindros detalladas arriba son aplicadas para resolver los siguientes ejercicios. Cada ejercicio tiene su respectiva solución, en donde se detalla el proceso y razonamiento usados.
EJERCICIO 1
¿Cuál es el volumen de un cilindro que tiene un radio de 5 m y una altura de 10 m?
Solución
Tenemos los siguientes datos:
- Radio, $latex r=5$
- Altura, $latex h=10$
Usando la fórmula del volumen con estos datos, tenemos:
$latex V=\pi {{r}^2}\times h$
$latex V=\pi {{(5)}^2}\times 10$
$latex V=\pi (25)\times 10$
$latex V=785.4$
El volumen es igual a 785.4 m³.
EJERCICIO 2
Si es que un cilindro tiene un radio de 6 m y una altura de 8 m, ¿cuál es su volumen?
Solución
Tenemos la siguiente información:
- Radio, $latex r=6$
- Altura, $latex h=8$
Al sustituir estos valores en la fórmula del volumen, tenemos:
$latex V=\pi {{r}^2}\times h$
$latex V=\pi {{(6)}^2}\times 8$
$latex V=\pi (36)\times 8$
$latex V=904.8$
El volumen es igual a 904.8 m³.
EJERCICIO 3
¿Cuál es el volumen de un cubo que tiene un diámetro de 8 m y una altura de 12 m?
Solución
Tenemos los siguientes valores:
- Diámetro, $latex d=8$
- Altura, $latex h=12$
En este caso, usamos la segunda fórmula del volumen ya que tenemos el diámetro del cilindro:
$latex V=\pi (\frac{{{d}^2}}{4})\times h$
$latex V=\pi (\frac{{{(8)}^2}}{4})\times 12$
$latex V=\pi (\frac{64}{4})\times 12$
$latex V=\pi (16)\times 12$
$latex V=603.2$
El volumen es igual a 603.2 m³.
EJERCICIO 4
¿Cuál es el volumen de un cilindro que tiene un diámetro de 12 m y una altura de 11 m?
Solución
Tenemos la siguiente información:
- Diámetro, $latex d=12$
- Altura, $latex h=11$
Usamos esos valores en la segunda fórmula del volumen:
$latex V=\pi (\frac{{{d}^2}}{4})\times h$
$latex V=\pi (\frac{{{(12)}^2}}{4})\times 11$
$latex V=\pi (\frac{144}{4})\times 11$
$latex V=\pi (36)\times 11$
$latex V=1244.1$
El volumen es igual a 1244.1 m³.
EJERCICIO 5
Un cilindro hueco tiene una altura de 15 m, un radio interno de 5 m y un radio externo de 6 m. ¿Cuál es su volumen?
Solución
Tenemos la siguiente información:
- Altura, $latex h=15$
- Radio externo, $latex r_{1}=6$
- Radio interno, $latex r_{2}=5$
Tenemos un cilindro hueco, por lo que tenemos que usar la tercera fórmula del volumen con los valores dados:
$latex V=\pi h({{r_{1}}^2}-{{r_{2}}^2})$
$latex V=\pi (15)({{6}^2}-{{5}^2})$
$latex V=\pi (15)(36-25)$
$latex V=\pi (15)(11)$
$latex V=518.4$
El volumen es igual a 518.4 m³.
EJERCICIO 6
¿Cuál es el volumen de un cilindro hueco que tiene una altura de 20 m, un radio interno de 6 m y un radio externo de 8 m?
Solución
Tenemos los siguientes valores:
- Altura, $latex h=20$
- Radio externo, $latex r_{1}=8$
- Radio interno, $latex r_{2}=6$
Usamos la tercera fórmula del volumen con estos valores:
$latex V=\pi h({{r_{1}}^2}-{{r_{2}}^2})$
$latex V=\pi (20)({{8}^2}-{{6}^2})$
$latex V=\pi (20)(64-36)$
$latex V=\pi (20)(28)$
$latex V=1759.3$
El volumen es igual a 1759.3 m³.
Ejercicios de volumen de cilindros para resolver
Usa las fórmulas del volumen de cilindros para resolver los siguientes ejercicios. Selecciona una respuesta y verifícala para comprobar que obtuviste la respuesta correcta. Si necesitas ayuda con esto, puedes mirar los ejercicios resueltos de arriba.
Véase también
¿Interesado en aprender más sobre cilindros? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
