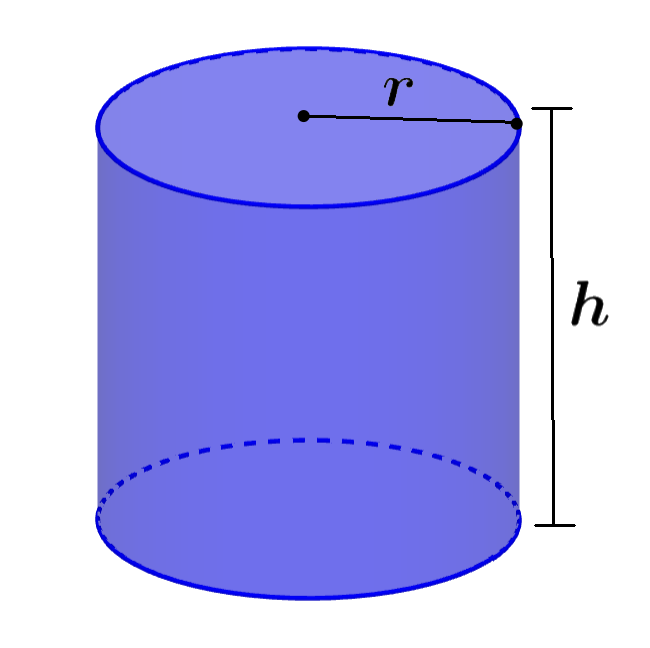
El cilindro es una de las figuras 3D básicas, el cual tiene dos bases circulares paralelas las cuales están ubicadas a una cierta distancia la una de la otra. Las dos bases circulares son unidas por una superficie curvada. El segmento de línea que une a los dos centros de los círculos es el eje del cilindro. La distancia entre las dos bases circulares es igual a la altura del cilindro. Dado que el cilindro es una figura 3D, tiene dos propiedades básicas más importantes, el volumen y el área superficial.
A continuación, conoceremos algunas de las características más importantes de los cilindros. Además, aprenderemos sobre las fórmulas del volumen y del área superficial y las usaremos para resolver algunos ejercicios.
GEOMETRÍA
Relevante para…
Conocer las características fundamentales de los cilindros.
GEOMETRÍA
Relevante para…
Conocer las características fundamentales de los cilindros.
Definición de un cilindro
Un cilindro es un sólido tridimensional que contiene dos bases paralelas conectadas por una superficie curvada. Las bases tienen usualmente una forma circular. La distancia perpendicular entre las bases es denotada como la altura “h” del cilindro y “r” es el radio del cilindro.
Características principales de un cilindro
Las siguientes son algunas de las características más importantes de los cilindros:
- Las bases del cilindro siempre son congruentes y paralelas la una de la otra.
- Si es que el eje del cilindro es un ángulo recto en la base, entonces, es llamado un “cilindro recto”.
- Si es que una de las bases tiene una inclinación y el eje no produce un ángulo recto en las bases, entonces, es llamado un “cilindro oblícuo”.
- Si es que las bases son circulares, entonces, es llamado un “cilindro circular”.
- Las bases de un cilindro también pueden ser elipses. Si es que la base del cilindro es elíptica, es llamado un “cilindro elíptico”.
- Un cilindro es similar a un prisma en el sentido que tiene la misma sección transversal en todas partes.
Fórmulas importantes de cilindros
Los cilindros son figuras tridimensionales, por lo que tienen dos propiedades importantes: el volumen y el área superficial.
Fórmula del volumen
Podemos calcular el volumen de un cilindro al multiplicar el área de las bases por la altura. En el caso de cilindros circulares, el área de las bases está dada por πr². Entonces, el volumen de un cilindro es:
| $latex V=\pi {{r}^2}\times h$ |
en donde, r representa a la longitud del radio de las bases circulares y h es la altura del cilindro.
Fórmula del área superficial
El área superficial es igual a toda la superficie ocupada por el cilindro. Podemos calcular el área superficial al sumar el área de las dos caras circulares y el área de la superficie curvada lateral.
Cada círculo tiene un área de πr² y la superficie lateral tiene un área de 2πrh, por lo que el área superficial total es:
| $latex A_{s}=2\pi {{r}^2}+2\pi r h$ |
Ejercicios de cilindros resueltos
Los siguientes ejercicios son resueltos aplicando las fórmulas de cilindros vistas arriba.
EJERCICIO 1
¿Cuál es el volumen de un cilindro que tiene un radio de 4 m y una altura de 5 m?
Solución: Tenemos las longitudes $latex r=4$ y $latex h=5$. Entonces, usamos estos valores en la fórmula del volumen:
$latex V=\pi {{r}^2}\times h$
$latex V=\pi {{(4)}^2}\times 5$
$latex V=\pi (16)\times 5$
$latex V=251.3$
El volumen del cilindro es 251.3 m³.
EJERCICIO 2
Si es que un cilindro tiene un radio de 7 m y una altura de 10 m, ¿cuál es su volumen?
Solución: Usamos la fórmula del volumen con los datos dados:
$latex V=\pi {{r}^2}\times h$
$latex V=\pi {{(7)}^2}\times 10$
$latex V=\pi (49)\times 10$
$latex V=1539.4$
El volumen del cilindro es 1539.4 m³.
EJERCICIO 3
Un cilindro tiene un radio de 6 m y una altura de 7 m. ¿Cuál es su área superficial?
Solución: Tenemos las longitudes $latex r=6$ y $latex h=7$, por lo que usamos estos valores en la fórmula del área superficial:
$latex A_{s}=2\pi {{r}^2}+2\pi r h$
$latex A_{s}=2\pi {{(6)}^2}+2\pi (6)(7)$
$latex A_{s}=226.2+263.9$
$latex A_{s}=490.1$
El área superficial es 490.1 m².
EJERCICIO 4
¿Cuál es el área superficial de un cilindro que tiene un radio de 8 m y una altura de 9 m?
Solución: Podemos usar los valores dados en la fórmula del área superficial:
$latex A_{s}=2\pi {{r}^2}+2\pi r h$
$latex A_{s}=2\pi {{(8)}^2}+2\pi (8)(9)$
$latex A_{s}=402.1+452.4$
$latex A_{s}=854.5$
El área superficial es 854,5 m².
Véase también
¿Interesado en aprender más sobre cilindros? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
