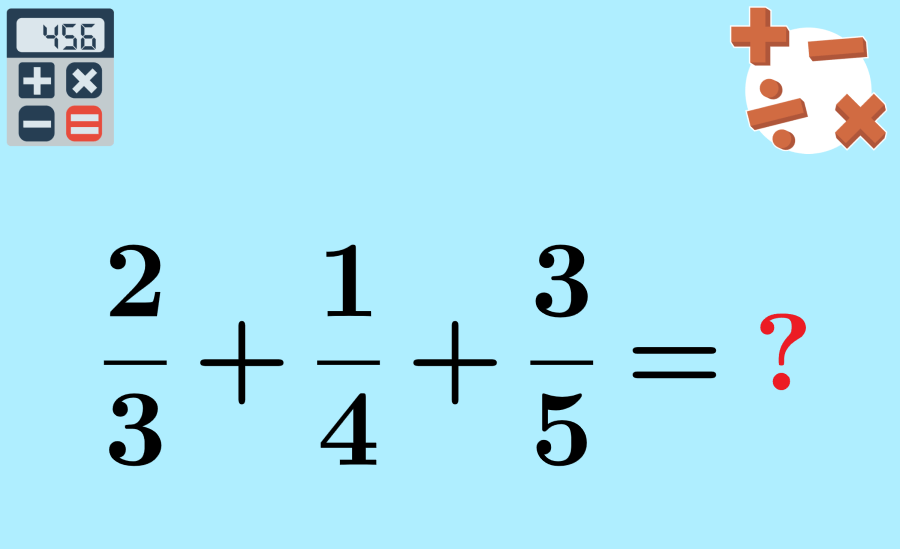Las fracciones heterogéneas son fracciones que tienen distintos denominadores. Para sumar este tipo de fracciones, tenemos que encontrar el mínimo común denominador de las fracciones. Luego, escribimos fracciones equivalentes usando el nuevo denominador y sumamos a las fracciones homogéneas (con el mismo denominador).
A continuación, veremos los pasos que podemos usar para sumar fracciones de distinto denominador. Además, resolveremos varios ejercicios de práctica para aprender los conceptos.
Pasos para sumar fracciones heterogéneas
Podemos sumar dos o más fracciones con diferentes denominadores al seguir los siguientes pasos:
Paso 1: Encontrar el mínimo común denominador (MCD) de las fracciones.
Paso 2: Dividir al MCD por el denominador de cada fracción.
Paso 3: Multiplicar tanto al numerador, como al denominador por el resultado del paso 2.
Paso 4: Sumar las fracciones homogéneas obtenidas del paso 3.
Paso 5: Simplificar la fracción final si es que es posible.
Sumar fracciones heterogéneas – Ejercicios resueltos
Los siguientes ejercicios son resueltos usando los pasos para sumar fracciones heterogéneas vistas arriba. Intenta resolver los ejercicios antes de mirar la solución.
EJERCICIO 1
¿Cuál es el resultado de la suma $latex \frac{1}{2}+\frac{1}{3}$?
Solución
Paso 1: El mínimo común denominador de 2 y 3 es 6.
Paso 2: Dividiendo a 6 por 2 (denominador de la primera fracción), tenemos 3. Al dividir a 6 por 3 (denominador de la segunda fracción), tenemos 2.
Paso 3: Multiplicando al numerador y al denominador de cada fracción por los números obtenidos en el paso 2, tenemos:
$$\frac{1\times 3}{2 \times 3}+\frac{1 \times 2}{3 \times 2}$$
$$=\frac{3}{6}+\frac{2}{6}$$
Paso 4: Sumando las fracciones del paso 3, tenemos:
$$\frac{3}{6}+\frac{2}{6}$$
$$=\frac{3+2}{6}$$
$$=\frac{5}{6}$$
Paso 5: La fracción ya está simplificada.
EJERCICIO 2
Resuelve la suma de fracciones $latex \frac{2}{3}+\frac{1}{4}$.
Solución
Paso 1: El MCD de 3 y 4 es 12.
Paso 2: Al dividir a 12 por 3 (denominador de la primera fracción), tenemos 4. Dividiendo a 12 por 4 (denominador de la segunda fracción), tenemos 3.
Paso 3: Al multiplicar tanto al numerador como al denominador de cada fracción por los números obtenidos en el paso 2, tenemos:
$$\frac{2\times 4}{3 \times 4}+\frac{1 \times 3}{4 \times 3}$$
$$=\frac{8}{12}+\frac{3}{12}$$
Paso 4: Sumando las fracciones homogéneas del paso 3, tenemos:
$$\frac{8}{12}+\frac{3}{12}$$
$$=\frac{8+3}{12}$$
$$=\frac{11}{12}$$
Paso 5: La fracción ya está simplificada.
EJERCICIO 3
Encuentra el resultado de la suma $latex \frac{3}{4}+\frac{2}{5}$.
Solución
Paso 1: El mínimo común denominador de 4 y 5 es 20.
Paso 2: Dividiendo a 20 por 4 (denominador de la primera fracción), tenemos 5. Al dividir a 20 por 5 (denominador de la segunda fracción), tenemos 4.
Paso 3: Multiplicamos a los numeradores y denominadores por los números obtenidos en el paso 2:
$$\frac{3\times 5}{4 \times 5}+\frac{2 \times 4}{5 \times 4}$$
$$=\frac{15}{20}+\frac{8}{20}$$
Paso 4: Resolviendo la suma de fracciones homogéneas del paso 3, tenemos:
$$\frac{15}{20}+\frac{8}{20}$$
$$=\frac{15+8}{20}$$
$$=\frac{23}{20}$$
Paso 5: Podemos escribir a la fracción como número mixto:
$$=1\frac{3}{20}$$
EJERCICIO 4
Encuentra el resultado de $latex \frac{1}{3}+\frac{1}{4}+\frac{1}{2}$.
Solución
Paso 1: El mínimo común denominador de 3, 4 y 2 es 12.
Paso 2: Al dividir a 12 por 3 (primer denominador), tenemos 4. Al dividir a 12 por 4 (segundo denominador), tenemos 3. Al dividir a 12 por 2 (tercer denominador), tenemos 6.
Paso 3: Multiplicamos a los numeradores y denominadores de cada fracción por los números obtenidos en el paso 2:
$$\frac{1\times 4}{3 \times 4}+\frac{1 \times 3}{4 \times 3}+\frac{1 \times 6}{2 \times 6}$$
$$=\frac{4}{12}+\frac{3}{12}+\frac{6}{12}$$
Paso 4: Resolviendo la suma de fracciones homogéneas del paso 3, tenemos:
$$\frac{4}{12}+\frac{3}{12}+\frac{6}{12}$$
$$=\frac{4+3+6}{12}$$
$$=\frac{13}{12}$$
Paso 5: Escribiendo como número mixto, tenemos:
$$=1\frac{1}{12}$$
EJERCICIO 5
Resuelve la suma de fracciones $latex \frac{2}{5}+\frac{3}{4}+\frac{1}{2}$.
Solución
Paso 1: El mínimo común denominador de 5, 4 y 2 es 20.
Paso 2: Al dividir a 20 por 5 (primer denominador), tenemos 4. Al dividir a 20 por 4 (segundo denominador), tenemos 5. Al dividir a 20 por 2 (tercer denominador), tenemos 10.
Paso 3: Al multiplicar tanto al numerador como al denominador de cada fracción por los números obtenidos en el paso 2, tenemos:
$$\frac{2\times 4}{5 \times 4}+\frac{3 \times 5}{4 \times 5}+\frac{1 \times 10}{2 \times 10}$$
$$=\frac{8}{20}+\frac{15}{20}+\frac{10}{20}$$
Paso 4: Resolviendo la suma de fracciones obtenidas en el paso 3, tenemos:
$$\frac{8}{20}+\frac{15}{20}+\frac{10}{20}$$
$$=\frac{8+15+10}{20}$$
$$=\frac{33}{20}$$
Paso 5: Escribiendo como número mixto, tenemos:
$$=1\frac{13}{20}$$
EJERCICIO 6
Resuelve la suma de fracciones $latex \frac{3}{4}+\frac{2}{3}+\frac{4}{5}+\frac{1}{2}$.
Solución
Paso 1: El mínimo común denominador de 4, 3, 5 y 2 es 60.
Paso 2: Al dividir a 60 por 4 (primer denominador), tenemos 15. Al dividir a 60 por 3 (segundo denominador), tenemos 20. Al dividir a 60 por 5 (tercer denominador), tenemos 12. Al dividir a 60 por 2, tenemos 30.
Paso 3: Multiplicamos a los numeradores y denominadores de cada fracción por los números obtenidos en el paso 2:
$$\frac{3\times 15}{4 \times 15}+\frac{2 \times 20}{3 \times 20}+\frac{4 \times 12}{5 \times 12}+\frac{1 \times 30}{2 \times 30}$$
$$=\frac{45}{60}+\frac{40}{60}+\frac{48}{60}+\frac{30}{60}$$
Paso 4: Al resolver la suma del paso 3, tenemos:
$$\frac{45}{60}+\frac{40}{60}+\frac{48}{60}+\frac{30}{60}$$
$$=\frac{45+40+48+30}{60}$$
$$=\frac{163}{60}$$
Paso 5: Escribiendo como número mixto, tenemos:
$$=2\frac{43}{60}$$
→ Calculadora de Suma de Fracciones
Suma de fracciones heterogéneas – Ejercicios para resolver
Resuelve los siguientes ejercicios aplicando el proceso usado para resolver una suma de fracciones heterogéneas.
Véase también
¿Interesado en aprender más sobre sumas de fracciones? Puedes mirar estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
