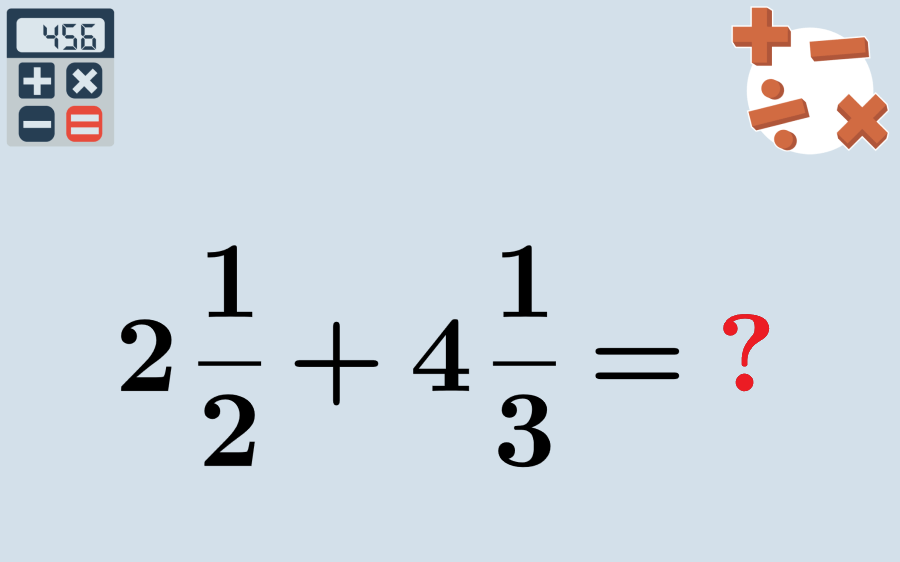Las fracciones que tienen números enteros, también llamadas fracciones mixtas, pueden ser sumadas siguiendo un proceso similar a cuando sumamos fracciones normales con un paso adicional. Primero, tenemos que convertir las fracciones mixtas a fracciones impropias. Luego, dependiendo de si las fracciones son homogéneas o heterogéneas, usaremos un proceso diferente.
A continuación, aprenderemos a sumar fracciones mixtas, homogéneas y heterogéneas. Además, resolveremos algunos ejercicios de práctica para aplicar estos conceptos.
Pasos para sumar fracciones mixtas
Las fracciones mixtas se caracterizan por tener números enteros. Si es que los denominadores de las fracciones son iguales, tenemos fracciones homogéneas y si es que los denominadores son diferentes, tenemos fracciones heterogéneas.
Para sumar fracciones mixtas, podemos seguir los siguientes pasos.
Paso 1: Convertir las fracciones mixtas a fracciones impropias. Para esto, multiplicamos el número entero por el denominador de la fracción y sumamos el resultado al numerador.
Paso 2: Determinar si es que las fracciones son homogéneas o heterogéneas. Si es que las fracciones son homogéneas, continuar al paso 6.
Paso 3: Si las fracciones son heterogéneas, tenemos que encontrar el mínimo común denominador (MCD) de las fracciones.
Paso 4: Dividir al MCD por el denominador de cada fracción.
Paso 5: Multiplicar tanto al numerador, como al denominador por el resultado del paso 4. Con esto, obtendremos fracciones homogéneas, en donde el denominador es el MCD.
Paso 6: Sumar las fracciones homogéneas. Para esto, usamos un solo denominador y sumamos los numeradores.
Paso 7: Simplificar la fracción final si es que es posible.
Sumar fracciones mixtas – Ejercicios resueltos
Los siguientes ejercicios son resueltos aplicando lo aprendido sobre la suma de fracciones mixtas. Intenta resolver los ejercicios tú mismo antes de mirar la solución.
EJERCICIO 1
Resuelve la suma de fracciones $latex 1\frac{1}{2}+\frac{1}{2}$.
Solución
Paso 1: Convirtiendo las fracciones mixtas a impropias, tenemos:
$$1\frac{1}{2}+\frac{1}{2}$$
$$=\frac{3}{2}+\frac{1}{2}$$
Paso 2: Ambos denominadores son igual a 2, por lo que las fracciones son homogéneas. Entonces, continuamos al paso 6.
Pasos 3-5: No aplica.
Paso 6: Para sumar las fracciones homogéneas, combinamos a los denominadores y sumamos los numeradores:
$$=\frac{3}{2}+\frac{1}{2}$$
$$=\frac{3+1}{2}$$
$$=\frac{4}{2}$$
Paso 7: Simplificando, tenemos:
$$=2$$
EJERCICIO 2
Encuentra el resultado a la suma $latex 2\frac{2}{3}+1\frac{1}{3}$.
Solución
Paso 1: Vamos a convertir las fracciones mixtas a fracciones impropias:
$$2\frac{2}{3}+1\frac{1}{3}$$
$$=\frac{8}{3}+\frac{4}{3}$$
Paso 2: Las fracciones son homogéneas, ya que ambos denominadores son igual a 3. Entonces, continuamos al paso 6.
Pasos 3-5: No aplica.
Paso 6: Sumamos las fracciones homogéneas al combinar a los denominadores y sumar a los numeradores:
$$=\frac{8}{3}+\frac{4}{3}$$
$$=\frac{8+4}{3}$$
$$=\frac{12}{3}$$
Paso 7: Podemos simplificar la fracción:
$$=4$$
EJERCICIO 3
Resuelve la suma de fracciones $latex 1\frac{2}{3}+\frac{1}{5}$.
Solución
Paso 1: Al convertir a las fracciones mixtas a impropias, tenemos:
$$1\frac{2}{3}+\frac{1}{5}$$
$$=\frac{5}{3}+\frac{1}{5}$$
Paso 2: En este caso, tenemos fracciones heterogéneas porque los denominadores son diferentes. Entonces, continuamos al paso 3.
Paso 3: El mínimo común denominador de 3 y 5 es 15.
Paso 4: Al dividir a 15 por 3 (primer denominador), tenemos 5. Al dividir a 15 por 5 (segundo denominador), tenemos 3.
Paso 5: Multiplicamos al numerador y al denominador por los números obtenidos en el paso 4, 5 para la primera fracción y 3 para la segunda:
$$=\frac{5\times 5}{3\times 5}+\frac{1\times 3}{5\times 3}$$
$$=\frac{25}{15}+\frac{3}{15}$$
Paso 6: Sumamos las fracciones homogéneas al combinar a los denominadores y sumar a los numeradores:
$$=\frac{25}{15}+\frac{3}{15}$$
$$=\frac{25+3}{15}$$
$$=\frac{28}{15}$$
Paso 7: Podemos simplificar al escribir como número mixto:
$$=1 \frac{13}{15}$$
EJERCICIO 4
Resuelve la suma de fracciones mixtas $latex 2\frac{3}{4}+4\frac{1}{2}$.
Solución
Paso 1: Convirtiendo a las fracciones mixtas a impropias, tenemos:
$$2\frac{3}{4}+4\frac{1}{2}$$
$$=\frac{11}{4}+\frac{9}{2}$$
Paso 2: Tenemos fracciones heterogéneas porque los denominadores son diferentes, por lo que continuamos al paso 3.
Paso 3: El mínimo común denominador de 4 y 2 es 4.
Paso 4: Dividiendo a 4 por 4 (primer denominador), tenemos 1. Dividiendo a 4 por 2 (segundo denominador), tenemos 2.
Paso 5: Al multiplicar al numerador y al denominador por los números obtenidos en el paso 4, tenemos:
$$=\frac{11\times 1}{4\times 1}+\frac{9\times 2}{2\times 2}$$
$$=\frac{11}{4}+\frac{18}{4}$$
Paso 6: Al sumar a las fracciones homogéneas, tenemos:
$$=\frac{11+18}{4}$$
$$=\frac{29}{4}$$
Paso 7: Podemos simplificar al escribir como número mixto:
$$=7 \frac{1}{4}$$
EJERCICIO 5
Resuelve la suma de fracciones mixtas $latex 1\frac{2}{5}+\frac{3}{5}+3\frac{1}{5}$.
Solución
Paso 1: Convirtiendo a las fracciones mixtas en fracciones impropias, tenemos:
$$1\frac{2}{5}+\frac{3}{5}+3\frac{1}{5}$$
$$=\frac{7}{5}+\frac{3}{5}+\frac{16}{5}$$
Paso 2: Aquí, tenemos fracciones homogéneas, por lo que continuamos al paso 6.
Pasos 3-5: No aplica.
Paso 6: Combinando a los denominadores y sumando a los numeradores, tenemos:
$$=\frac{7}{5}+\frac{3}{5}+\frac{16}{5}$$
$$=\frac{7+3+16}{5}$$
$$=\frac{26}{5}$$
Paso 7: Podemos simplificar la fracción al convertirla en fracción mixta:
$$=5\frac{1}{5}$$
EJERCICIO 6
Resuelve la suma de fracciones $latex 2\frac{3}{4}+1\frac{2}{3}+1\frac{4}{5}$.
Solución
Paso 1: Al convertir a las fracciones mixtas a impropias, tenemos:
$$2\frac{3}{4}+1\frac{2}{3}+1\frac{4}{5}$$
$$=\frac{11}{4}+\frac{5}{3}+\frac{9}{5}$$
Paso 2: Tenemos tres fracciones heterogéneas, por lo que continuamos al paso 3.
Paso 3: El mínimo común denominador de 4, 3 y 5 es 60.
Paso 4: Al dividir a 60 por 4 (primer denominador), tenemos 15. Al dividir a 60 por 3 (segundo denominador), tenemos 20. Al dividir a 60 por 5 (tercer denominador), tenemos 12.
Paso 5: Multiplicamos a los numeradores y a los denominadores de las fracciones por los números obtenidos en el paso 4, tenemos:
$$=\frac{11\times 15}{4\times 15}+\frac{5\times 20}{3\times 20}+\frac{9\times 12}{5\times 12}$$
$$=\frac{165}{60}+\frac{100}{60}+\frac{108}{60}$$
Paso 6: Sumando las fracciones homogéneas, tenemos:
$$=\frac{165+100+108}{60}$$
$$=\frac{373}{60}$$
Paso 7: Podemos simplificar al escribir como número mixto:
$$=6 \frac{13}{60}$$
Suma de fracciones mixtas – Ejercicios para resolver
Resuelve las siguientes sumas de fracciones mixtas. Si tienes problema con estos ejercicios, puedes usar los ejercicios resueltos de arriba como guía.
Véase también
¿Interesado en aprender más sobre sumas de fracciones? Puedes mirar estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
