Un sistema de ecuaciones consiste de dos o más ecuaciones con dos o más variables, las cuales comparten la misma solución. Uno de los métodos usados para resolver sistemas de dos ecuaciones con dos variables es el método de reducción. Este método consiste en multiplicar a una de las ecuaciones por un número, de modo que al sumar las ecuaciones, eliminemos una de las variables.
A continuación, aprenderemos a resolver sistemas de ecuaciones usando el método de reducción. Luego, resolveremos varios ejercicios de práctica usando este método.
ÁLGEBRA
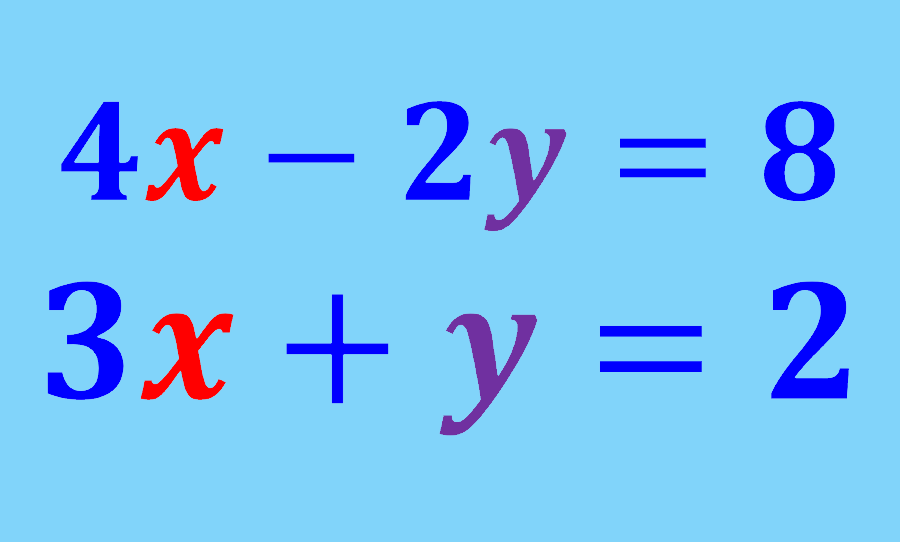
Relevante para…
Aprender a resolver sistemas de ecuaciones con el método de reducción.
ÁLGEBRA
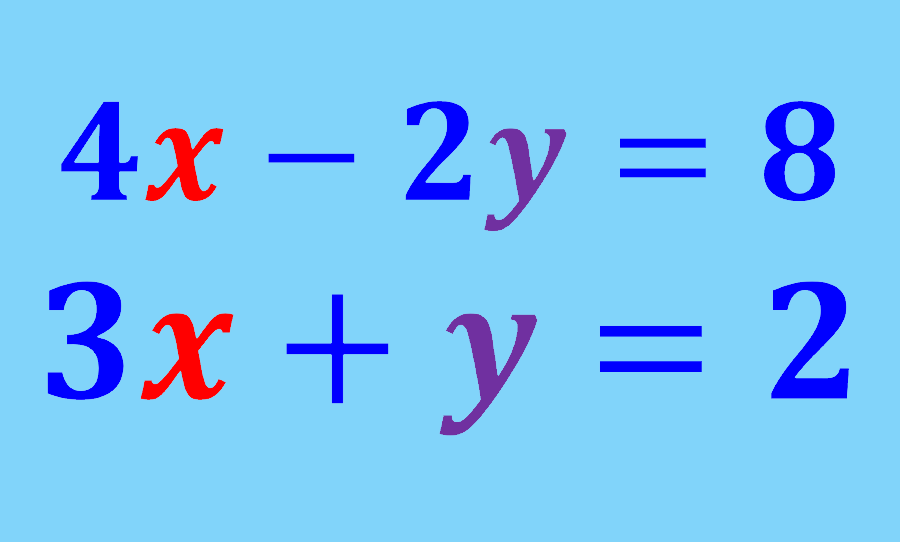
Relevante para…
Aprender a resolver sistemas de ecuaciones con el método de reducción.
Pasos para resolver sistemas de ecuaciones por reducción
El método de reducción para resolver sistemas de ecuaciones consiste en multiplicar a una de las ecuaciones por un número, de modo que al sumar ambas ecuaciones, una de las variables sea eliminada.
Detalladamente, podemos seguir los siguientes pasos para resolver sistemas de ecuaciones por reducción o eliminación:
1. Simplificar ambas ecuaciones.
Esto incluye remover paréntesis, eliminar fracciones y combinar términos semejantes.
2. Escribir a las ecuaciones en la forma Ax+By=C para facilitar su resolución.
3. Manipular las ecuaciones para obtener coeficientes opuestos en una de las variables.
Tenemos que eliminar una de las variables al sumar las ecuaciones. Por lo tanto, tenemos que lograr que un coeficiente sea a y el otro –a en una de las variables.
Por ejemplo, si tenemos 2x en una ecuación y 3x en la otra, multiplicamos por 3 a la primera y por -2 a la segunda para obtener 6 y -6 respectivamente.
4. Sumar las ecuaciones.
Al hacer esto, obtendremos una sola ecuación con una sola variable.
5. Resuelve la ecuación del paso 4 para la variable restante.
Si necesitas hacer una revisión, puedes mirar nuestro artículo sobre cómo resolver ecuaciones con una incógnita.
6. Encuentra el valor de la segunda variable.
Sustituye el valor del paso 5 en cualquiera de las dos ecuaciones y resuelve para la segunda variable.
Ejercicios resueltos de sistemas de ecuaciones por reducción
EJERCICIO 1
Usa el método de reducción para resolver el sistema: $latex \begin{cases}x-y=3 \\ 2x+y=12 \end{cases}$
Solución
Pasos 1 y 2: Las ecuaciones ya están simplificadas y ya están en la forma Ax+By=C.
Paso 3: Tenemos coeficientes opuestos en la variable y.
Paso 4: Sumando las ecuaciones, tenemos:
$latex x-y=3$
$latex + \hspace{1cm} 2x+y=12$
___________________
$latex 3x=15$
Paso 5: Resolviendo para x, tenemos:
$latex 3x=15$
$latex x=5$
Paso 6: Sustituyendo $latex x=5$ en la segunda ecuación, tenemos:
$latex 2x+y=12$
$latex 2(5)+y=12$
$latex 10+y=12$
$latex y=2$
La solución al sistema de ecuaciones es $latex x=5,~~y=2$.
EJERCICIO 2
Encuentra la solución al sistema de ecuaciones usando el método de eliminación: $latex \begin{cases}y=2x+7 \\ -6x-2y=-4 \end{cases}$
Solución
Paso 1: Podemos dividir a la segunda ecuación por -2:
$latex \begin{cases}y=2x+7 \\ 3x+y=2 \end{cases}$
Paso 2: Escribimos a las ecuaciones en la forma Ax+By=C:
$latex \begin{cases}-2x+y=7 \\ 3x+y=2 \end{cases}$
Paso 3: Multiplicamos la primera ecuación por -1 para obtener coeficientes opuestos en y:
$latex \begin{cases}2x-y=-7\\ 3x+y=2 \end{cases}$
Paso 4: Sumando las ecuaciones, tenemos:
$latex 2x-y=-7$
$latex + \hspace{1cm} 3x+y=2$
___________________
$latex 5x=-5$
Paso 5: Resolvemos para x:
$latex 5x=-5$
$latex x=-1$
Paso 6: Sustituyendo $latex x=-1$ en la primera ecuación, tenemos:
$latex y=2x+7$
$latex y=2(-1)+7$
$latex y=5$
La solución es $latex x=-1, ~~y=5$.
EJERCICIO 3
Resuelve el sistema de ecuaciones: $latex \begin{cases}2x=3y-14 \\ 2y=x+8 \end{cases}$
Solución
Paso 1: Las ecuaciones ya están simplificadas.
Paso 2: Escribiendo a las ecuaciones en la forma Ax+By=C, tenemos:
$latex \begin{cases}2x-3y=-14 \\ -x+2y=8 \end{cases}$
Paso 3: Multiplicamos la segunda ecuación por 2 para obtener coeficientes opuestos en x:
$latex \begin{cases}2x-3y=-14 \\ -2x+4y=16 \end{cases}$
Paso 4: Al sumar las ecuaciones, tenemos:
$latex 2x-3y=-14$
$latex + \hspace{1cm} -2x+4y=16$
___________________
$latex y=2$
Paso 5: Ya obtuvimos el valor de y:
$latex y=2$
Paso 6: Usando el valor $latex y=2$ en la primera ecuación, tenemos:
$latex 2x=3y-14$
$latex 2x=3(2)-14$
$latex 2x=-8$
$latex x=-4$
La solución es $latex x=-4,~~y=2$.
EJERCICIO 4
Resuelve el sistema de ecuaciones: $latex \begin{cases}2x-3y=7 \\ 2x+3y=1 \end{cases}$
Solución
Pasos 1 y 2: No tenemos nada que simplificar y las ecuaciones ya están en la forma Ax+By=C.
Paso 2: Ya tenemos coeficientes opuestos en y.
Paso 3: Sumando las ecuaciones, tenemos:
$latex 2x-3y=7$
$latex + \hspace{1cm} 2x+3y=1$
___________________
$latex 4x=8$
Paso 5: Resolviendo la ecuación, tenemos:
$latex x=2$
Paso 6: Usando el valor $latex x=2$ en la segunda ecuación, tenemos:
$latex 2x+3y=1$
$latex 2(2)+3y=1$
$latex 4+3y=1$
$latex 3y=-3$
$latex y=-1$
La solución es $latex x=2,~~y=-1$.
EJERCICIO 5
Encuentra la solución al sistema de ecuaciones: $latex \begin{cases}3x-y=1 \\ 5x+y=7 \end{cases}$
Solución
Paso 1 y 2: Las ecuaciones ya están simplificadas y escritas en la forma Ax+By=C.
Paso 3: Ya tenemos coeficientes opuestos en y:
$latex \begin{cases}3x-y=1 \\ 5x+y=7 \end{cases}$
Paso 4: Sumando las ecuaciones, tenemos:
$latex 3x-y=1$
$latex + \hspace{1cm} 5x+y=7$
___________________
$latex 8x=8$
Paso 5: Resolviendo para x, tenemos:
$latex x=1$
Paso 6: Usando el valor $latex x=1$ en la segunda ecuación, tenemos:
$latex 5x+y=7$
$latex 5(1)+y=7$
$latex y=2$
La solución es $latex x=1,~~y=2$.
EJERCICIO 6
Resuelve el sistema de ecuaciones: $latex \begin{cases}2x-7y=1 \\ 2x+3y=11 \end{cases}$
Solución
Paso 1 y 2: Las ecuaciones ya están simplificadas y escritas en la forma Ax+By=C.
Paso 3: Multiplicamos a la segunda ecuación por -1 para obtener coeficientes opuestos en x:
$latex \begin{cases}2x-7y=1 \\ -2x-3y=-11 \end{cases}$
Paso 4: Sumando las ecuaciones, tenemos:
$latex 2x-7y=1$
$latex + \hspace{1cm} -2x-3y=-11$
___________________
$latex -10y=-10$
Paso 5: Resolviendo la ecuación, tenemos:
$latex y=1$
Paso 6: Usando el valor $latex y=1$ en la primera ecuación, tenemos:
$latex 2x-7y=1$
$latex 2x-7(1)=1$
$latex 2x=8$
$latex x=4$
La solución es $latex x=4,~~y=1$.
EJERCICIO 7
Resuelve el sistema de ecuaciones: $latex \begin{cases}3x-4y=5 \\ 6x-4y=2 \end{cases}$
Solución
Paso 1: Podemos simplificar la segunda ecuación al dividirla por 2:
$latex \begin{cases}3x-4y=5 \\ 3x-2y=1 \end{cases}$
Paso 2: Las ecuaciones ya están en la forma Ax+By=C.
Paso 3: Multiplicamos la segunda ecuación por -1 para obtener coeficientes opuestos en x:
$latex \begin{cases}3x-4y=5 \\ -3x+2y=-1 \end{cases}$
Paso 4: Sumando las ecuaciones, tenemos:
$latex 3x-4y=5$
$latex + \hspace{1cm} -3x+2y=-1$
___________________
$latex -2y=4$
Paso 5: Resolviendo la ecuación, tenemos:
$latex y=-2$
Paso 6: Usando el valor $latex y=-2$ en la segunda ecuación, tenemos:
$latex 3x-2y=1$
$latex 3x-2(-2)=1$
$latex 3x+4=1$
$latex 3x=-3$
$latex x=-1$
La solución es $latex x=-1,~~y=-2$.
Sistemas de ecuaciones por reducción – Ejercicios para resolver
Resuelve el sistema de ecuaciones: $latex \begin{cases}3x-2y=5 \\ 2x+y=8 \end{cases}$
Escribe la respuesta en la forma x=?, y=?.
Véase también
¿Interesado en aprender más sobre sistemas de ecuaciones? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
