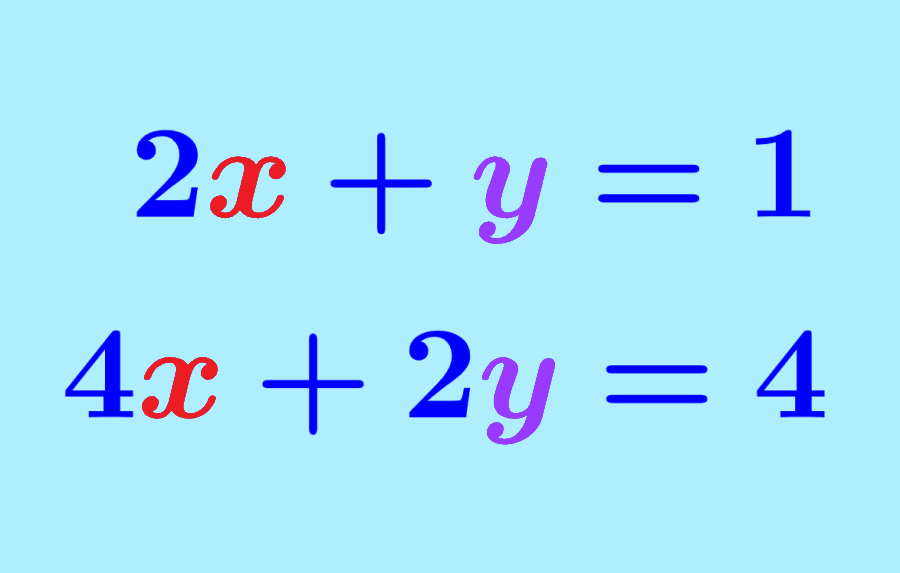Los sistemas de ecuaciones son un conjunto de dos o más ecuaciones con dos o más variables. Para encontrar la solución a un sistema de ecuaciones, tenemos que resolver a las ecuaciones simultáneamente. Sin embargo, no todos los sistemas de ecuaciones tienen una solución. Podemos tener sistemas sin soluciones o incluso sistemas con infinitas soluciones.
A continuación, aprenderemos cómo determinar cuando un sistema de ecuaciones tiene una solución, no tiene soluciones o tiene infinitas soluciones.
Sistemas de ecuaciones y sus soluciones
Los sistemas de ecuaciones son conjuntos de dos o más ecuaciones que tienen que ser resueltas simultáneamente. Una solución al sistema de ecuaciones tiene que satisfacer a todas las ecuaciones del sistema al mismo tiempo.
En el caso de sistemas de ecuaciones 2×2, una solución al sistema es un par ordenado $latex (x,~y)$ que hace que ambas ecuaciones sean verdaderas. Una solución es lo que las ecuaciones tienen en común, es el lugar en donde sus líneas se intersecan.
Si es que un par ordenado solo satisface una de las ecuaciones del sistema, pero no para la otra, entonces no es una solución al sistema de ecuaciones.
Dependiendo de si el sistema de ecuaciones tiene soluciones o no, podemos tener dos tipos de sistemas de ecuaciones, sistemas consistentes y sistemas inconsistentes.
- Un sistema consistente es un sistema que tiene por lo menos una solución.
- Un sistema inconsistente es un sistema que no tiene soluciones.
Hay tres posibles resultados que podemos encontrar al trabajar con sistemas de ecuaciones lineales:
1. Una solución
2. Ninguna solución
3. Infinitas soluciones.
Sistemas de ecuaciones con una única solución
En el caso de sistemas de dos ecuaciones con dos variables, un par ordenado $latex (x,~y)$ es una solución al sistema solo si es que satisface ambas ecuaciones. Es decir, al usar el par ordenado en cada una de las ecuaciones, ambas ecuaciones deben resultar verdaderas.
Un sistema de ecuaciones lineales de dos o más ecuaciones con dos o más variables tendrá una sola solución cuando las ecuaciones del sistema son diferentes la una de la otra y no son paralelas. Los detalles de estos casos son mostrados abajo.
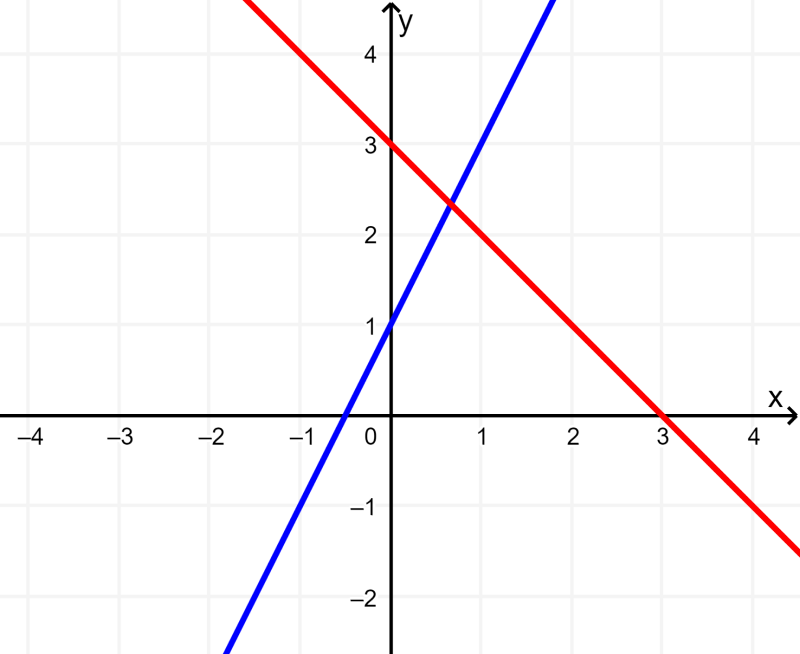
Cuando obtenemos una única solución al sistema de ecuaciones como respuesta final, el sistema es consistente. La siguiente gráfica muestra un sistema de dos ecuaciones con dos incógnitas que tiene una solución:
Podemos ver que las gráficas de las ecuaciones del sistema intersecan en un solo punto.
Entonces, en el caso de sistemas de ecuaciones lineales, una forma de determinar si el sistema tendrá una única solución es trazar gráficas simples de las ecuaciones y observar si es que las rectas intersecan en un solo punto.
EJEMPLOS
Ejemplos de sistemas de ecuaciones con una solución:
$latex \begin{cases}x+2y=10 \\ 2x-y=5 \end{cases}$, solución: $latex x=4,~~y=3$
$latex \begin{cases}-2x-y=1 \\ 3x+4y=6 \end{cases}$, solución: $latex x=-2, ~~y=3$
$latex \begin{cases}3x+4y-27=0 \\ 5x+y-11=0 \end{cases}$, solución: $latex x=1,~~y=6$
Sistemas de ecuaciones sin solución
Los sistemas de ecuaciones lineales pueden no tener una solución cuando las gráficas de sus ecuaciones son paralelas. Si es que las rectas de las ecuaciones son paralelas, las rectas nunca se intersecarán.
En estos casos, las ecuaciones del sistema no tienen ningún punto en común, por lo que no existe ninguna solución que pueda satisfacer a todas las ecuaciones del sistema. Este tipo de sistemas de ecuaciones son inconsistentes.
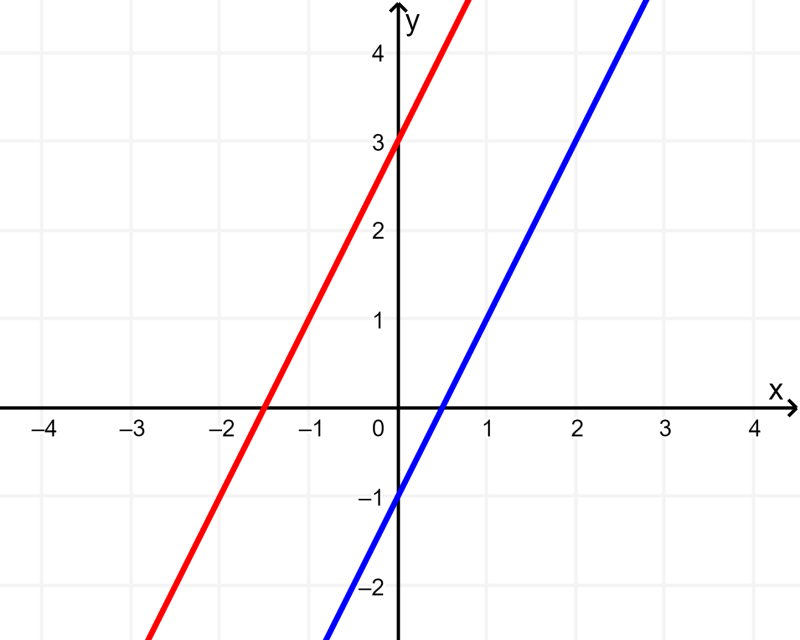
En la siguiente gráfica, podemos ver un sistema de dos ecuaciones con dos incógnitas que no tienen ninguna solución:
Podemos ver que las gráficas de las ecuaciones son paralelas y no se intersecan, por lo que no tienen ningún punto en común.
Entonces, cuando tenemos sistemas de ecuaciones lineales, podemos trazar gráficas simples de las ecuaciones para determinar si el sistema no tiene ninguna solución. Si es que por lo menos dos de las rectas son paralelas, el sistema no tiene solución.
Algebraicamente, podemos determinar si es que un sistema de ecuaciones lineales no tiene solución al comparar sus pendientes. Si es que las ecuaciones tienen la misma pendiente, las rectas serán paralelas.
EJEMPLOS
Ejemplos de sistemas de ecuaciones sin ninguna solución:
- $latex \begin{cases}x+y=10 \\ x+y=5 \end{cases}$
Al escribir a las ecuaciones en la forma $latex y=mx+b$, sabemos que la pendiente es m. En este caso, tenemos las ecuaciones $latex y=-x+10$ y $latex y=-x+5$.
Las pendientes de ambas ecuaciones son igual a -1. Entonces, las rectas son paralelas y el sistema de ecuaciones no tiene ninguna solución.
- $latex \begin{cases}-2x+y=1 \\ -4x+2y=6 \end{cases}$
Al escribir a las ecuaciones en la forma $latex y=mx+b$, tenemos $latex y=2x+1$ y $latex y=2x+3$. Entonces, sus pendientes son igual a 2, por lo que las rectas son paralelas y el sistema no tiene solución.
Sistemas de ecuaciones con infinitas soluciones
Un sistema de ecuaciones lineales tiene infinitas soluciones cuando las gráficas de las ecuaciones se sobreponen la una sobre la otra. Esto sucede cuando tenemos versiones equivalentes de la misma ecuación.
En este caso, tendremos dos o más ecuaciones lineales equivalentes, por lo que cualquier solución que funcione con la primera ecuación, también funcionará con la segunda.
Sistemas de ecuaciones que tiene un número infinito de soluciones son consistentes, ya que tienen por lo menos una sola solución.
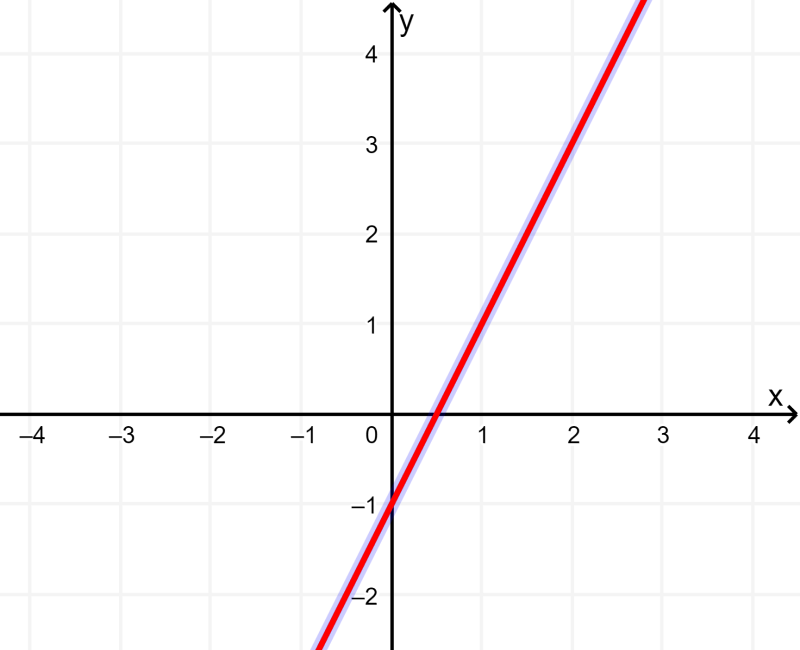
En la siguiente gráfica, podemos observar un sistema de dos ecuaciones con dos incógnitas que tiene un número infinito de soluciones:
Podemos observar que las rectas están sobrepuestas. Básicamente, esto significa que las ecuaciones dadas resultan en la misma recta al ser graficadas.
Entonces, para determinar si es que un sistema de ecuaciones tiene soluciones infinitas, podemos trazar gráficas básicas de las ecuaciones y observar si es que las ecuaciones se sobreponen.
Algebraicamente, podemos determinar si las ecuaciones del sistema son equivalentes al simplificarlas y manipularlas. Por ejemplo, podríamos tener que una de las ecuaciones es igual a la otra multiplicada por 2.
EJEMPLOS
Ejemplos de sistemas de ecuaciones con soluciones infinitas:
- $latex \begin{cases}x+y=3\\ 2x+2y=6 \end{cases}$
Las ecuaciones del sistema parecieran ser diferentes a primera vista. Sin embargo, la segunda ecuación es obtenida al multiplicar a la primera por 2. Entonces, estas ecuaciones son equivalentes y el sistema tendrá soluciones infinitas.
- $latex \begin{cases}-2x+y=1 \\ 6x-3y=-3 \end{cases}$
La segunda ecuación es obtenida al multiplicar a la primera por -3. Entonces, las ecuaciones son equivalentes y el sistema tendrá soluciones infinitas.
Véase también
¿Interesado en aprender más sobre sistemas de ecuaciones? Mira estas páginas: