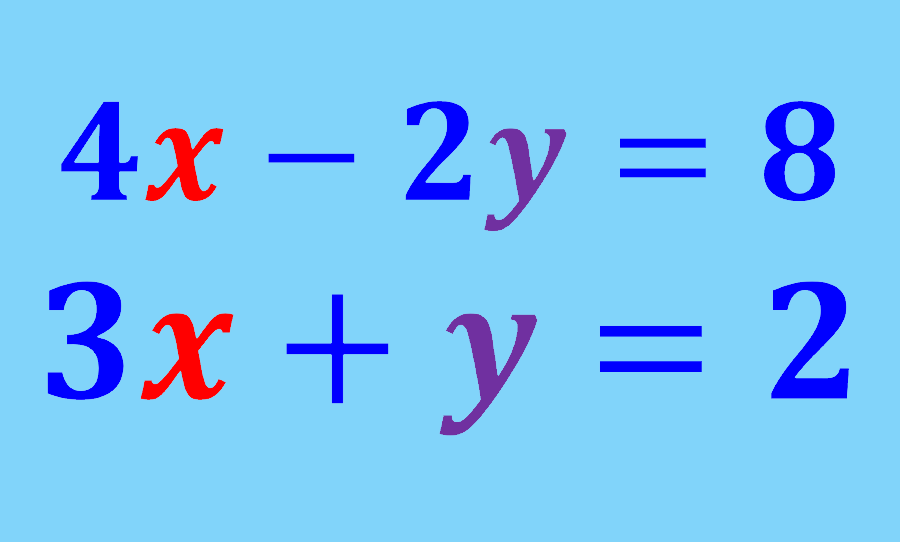Los sistemas de ecuaciones 2×2 son sistemas de dos ecuaciones con dos variables. Estos sistemas pueden ser resueltos usando tres métodos principales: el método gráfico, el método de sustitución y el método de eliminación o reducción.
En este artículo, aprenderemos sobre estos sistemas. Conoceremos cómo resolver sistemas de ecuaciones 2×2 usando los tres métodos mencionados.
Resolver sistemas de ecuaciones 2×2 gráficamente
Podemos seguir los siguientes pasos para resolver un sistema de ecuaciones 2×2 gráficamente:
1. Graficar la primera ecuación.
Puedes usar cualquier método para graficar una recta. Si es que lo necesitas, puedes mirar nuestra guía sobre cómo graficar funciones lineales.
2. Graficar la segunda ecuación en el mismo sistema de coordenadas que la primera.
3. Encuentra el punto de intersección.
- Si es que las líneas intersecan en un solo lugar, entonces el punto de intersección es la solución al sistema de ecuaciones.
- Si es que las líneas son paralelas, entonces nunca se intersecan y, por lo tanto, no hay ninguna solución.
- Si es que las líneas están una encima de la otra, entonces existe un número infinito de soluciones.
4. Verifica la solución al sistema en ambas ecuaciones.
Sustituye la solución en ambas ecuaciones. Si es que ambas ecuaciones resultan verdaderas, entonces la solución es verdadera. Si es que alguna de las ecuaciones resulta falsa, entonces ese par ordenado no es la solución correcta.
EJEMPLO 1
Resuelve el sistema de ecuaciones gráficamente: $latex \begin{cases}x+y=4 \\ 2x-y=-1 \end{cases}$
Solución
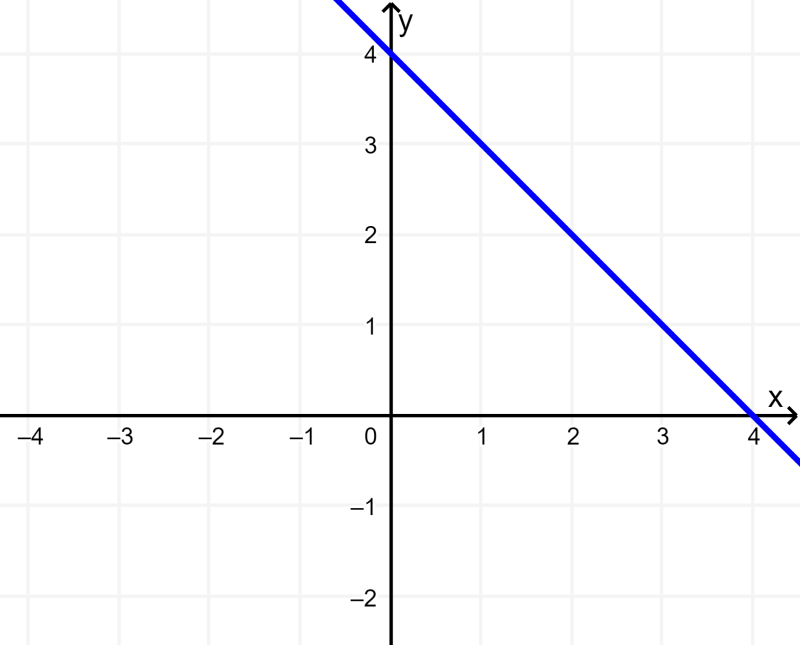
Paso 1: Graficar la primera ecuación.
Podemos reescribir la ecuación en la forma $latex y=mx+b$, en donde m es la pendiente y b es el intercepto en y.
$latex x+y=4$
$latex y=4-x$
Entonces, el intercepto en y es 4 y la pendiente es -1:
Paso 2: Graficar la segunda ecuación.
Usamos el mismo método que la ecuación anterior:
$latex 2x-y=-1$
$latex y=2x+1$
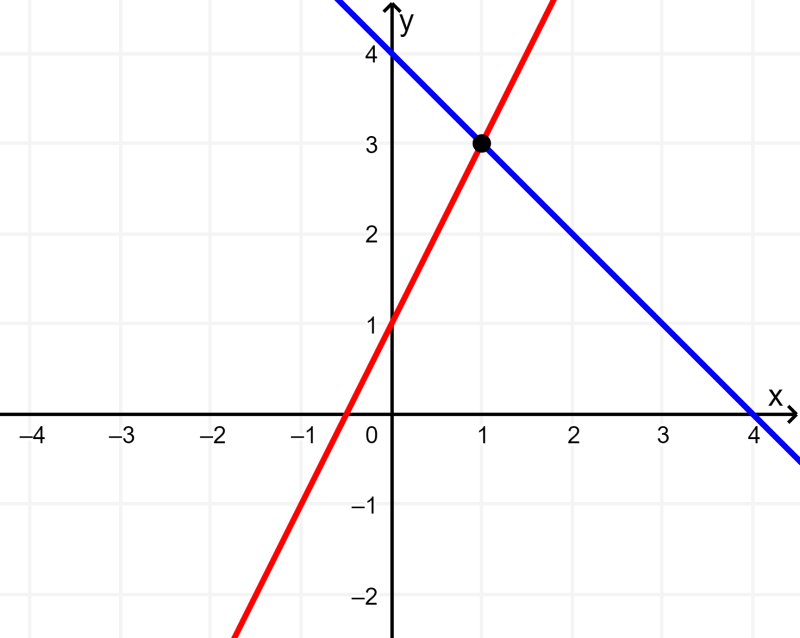
Entonces, el intercepto en y es 1 y la pendiente es 2:
Paso 3: Encuentra el punto de intersección.
Vemos que las ecuaciones se intersecan en el punto (1, 3).
Paso 4: Verifica el par de soluciones en ambas ecuaciones.
Fácilmente podemos verificar que al sustituir los valores de x=1 y y=3, ambas ecuaciones son verdaderas:
$latex x+y=4$
$latex 1+3=4$
$latex 4=4$
$latex 2x-y=-1$
$latex 2(1)-3=-1$
$latex -1=-1$
EJEMPLO 2
Resuelve el sistema de ecuaciones gráficamente: $latex \begin{cases}x+2y=7 \\ 3x-y=7 \end{cases}$
Solución
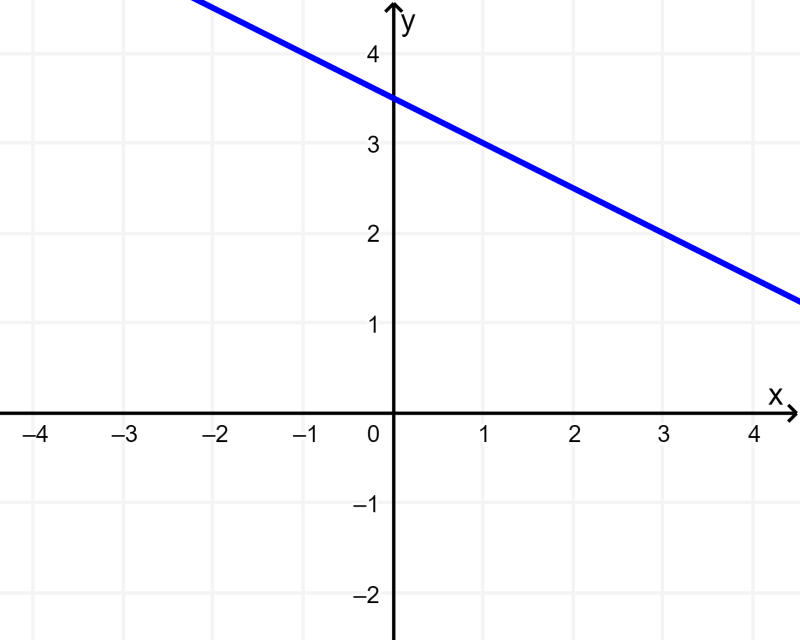
Paso 1: Graficar la primera ecuación.
Podemos reescribir la ecuación en la forma $latex y=mx+b$, en donde m es la pendiente y b es el intercepto en y.
$latex x+2y=7$
$latex y=-\frac{1}{2}x+\frac{7}{2}$
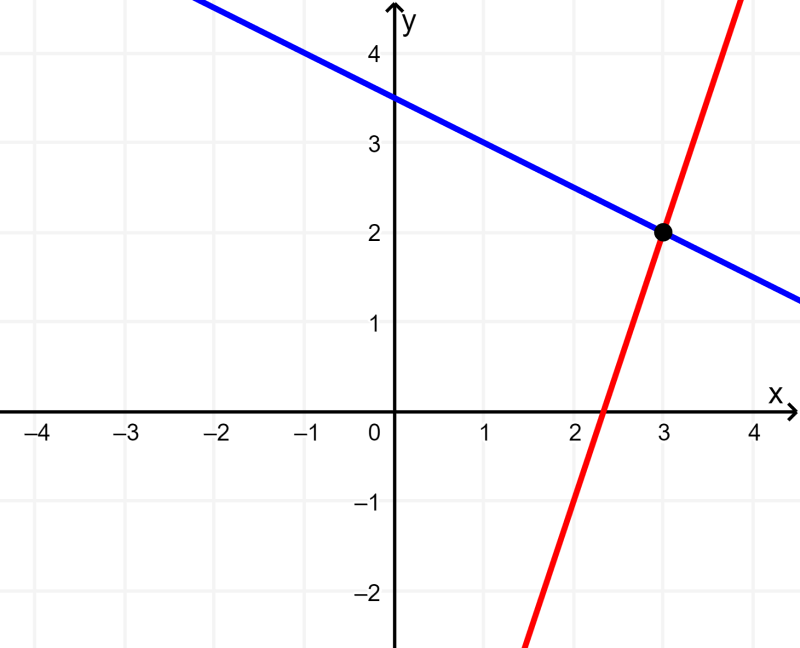
Entonces, el intercepto en y es 7/2 y la pendiente es -1/2:
Paso 2: Graficar la segunda ecuación.
Usamos el mismo método que la ecuación anterior:
$latex 3x-y=7$
$latex y=3x-7$
Entonces, el intercepto en y es -7 y la pendiente es 3:
Paso 3: Encuentra la solución.
Vemos que las ecuaciones se intersecan en el punto (3, 2).
Paso 4: Verifica el par de soluciones en ambas ecuaciones.
Fácilmente podemos verificar que al sustituir los valores de x=3 y y=2, ambas ecuaciones son verdaderas:
$latex x+2y=7$
$latex 3+2(2)=7$
$latex 7=7$
$latex 3x-y=7$
$latex 3(3)-2=7$
$latex 7=7$
Resolver sistemas de ecuaciones 2×2 por el método de sustitución
Sigue los siguientes pasos para resolver un sistema de ecuaciones 2×2 usando el método de sustitución:
1. Simplificar si es que es posible.
Esto incluye remover los paréntesis u otros signos de agrupación y combinar términos semejantes. Si es que tenemos fracciones, podemos multiplicar por el mínimo común múltiplo.
2. Resolver una ecuación para una variable.
No importa cuál ecuación escojamos o para cuál variable resolvamos. Si es que una de las ecuaciones ya tiene despejada una variable, podemos usar esa ecuación.
3. Sustituye la ecuación del paso 2 en la otra ecuación.
Asegúrate de sustituir en la ecuación que no usaste en el paso 2. Esto nos dará una ecuación con una sola variable.
4. Resuelve la ecuación del paso 2 para la variable restante.
Si necesitas ayuda con esto, puedes mirar nuestra guía sobre cómo resolver ecuaciones con una incógnita.
5. Resuelve para la segunda variable.
Sustituye el valor que encontraste en el paso 4 en cualquiera de las dos ecuaciones y resuelve para la otra variable.
6. Verifica la solución en ambas ecuaciones.
Sustituye los valores de las incógnitas en ambas ecuaciones. Si es que ambas ecuaciones son verdaderas, los valores son la solución correcta.
EJEMPLO 1
Resuelve el sistema de ecuaciones usando el método de sustitución: $latex \begin{cases}3x-5y=15 \\ y=2x+4 \end{cases}$
Solución
Paso 1: Simplificar si es que es posible. En este caso, ambas ecuaciones ya están simplificadas.
Paso 2: Resolver una ecuación para una variable. Podemos ver que la segunda ecuación ya está resuelta para la variable y:
$latex y=2x+4$
Paso 3: Sustituye lo que obtuviste en el paso 2 en la otra ecuación.
Sustituimos la expresión $latex y=2x+4$ en la primera ecuación:
$latex 3x-5y=15$
$latex 3x-5(2x+4)=15$
$latex 3x-10x-20=15$
Paso 4: Resuelve para la variable restante:
$latex 3x-10x-20=15$
$latex -7x=35$
$latex x=-5$
Paso 5: Resuelve para la segunda variable.
Sustituimos $latex x=-5$ en la segunda ecuación:
$latex y=2x+4$
$latex y=-10+4$
$latex y=-6$
Paso 6: Verifica la solución en ambas ecuaciones.
EJEMPLO 2
Resuelve el sistema de ecuaciones usando el método de sustitución: $latex \begin{cases}x-2y=3 \\ 2x-3y=7 \end{cases}$
Solución
Paso 1: Ambas ecuaciones ya están simplificadas.
Paso 2: Resolver una ecuación para una variable. Podemos ver resolver la primera ecuación para x:
$latex x-2y=3$
$latex x=3+2y$
Paso 3: Sustituimos la expresión $latex x=3+2y$ en la segunda ecuación:
$latex 2x-3y=7$
$latex 2(3+2y)-3y=7$
$latex 6+4y-3y=7$
Paso 4: Resuelve para la variable restante:
$latex 6+4y-3y=7$
$latex y=1$
Paso 5: Resuelve para la segunda variable. Sustituimos $latex y=1$ en la primera ecuación:
$latex x-2y=3$
$latex x-2(1)=3$
$latex x=5$
Paso 6: Verifica la solución en ambas ecuaciones.
Inténtalo tú mismo – Resuelve los ejercicios
Resolver sistemas de ecuaciones 2×2 por el método de eliminación
Sigue los siguientes pasos para resolver un sistema de ecuaciones 2×2 usando el método de sustitución:
1. Simplificar si es que es posible y coloca a las ecuaciones en la forma Ax+By=C.
Esto incluye remover los paréntesis u otros signos de agrupación y combinar términos semejantes. Si es que tenemos fracciones, podemos multiplicar por el mínimo común múltiplo.
2. Multiplica una o ambas ecuaciones por un número que creará coeficientes opuestos en una variable.
Vamos a sumar las ecuaciones y necesitamos que una de las variables se elimine luego de realizar la suma. Por ejemplo, si tenemos 2x en una ecuación y 3x en la segunda, podemos multiplicar por -3 la primera y por 2 la segunda, de ese modo obtenemos -6 en la primera y 6 en la segunda.
3. Suma las ecuaciones.
Al sumar las ecuaciones, una de las variables será eliminada y obtendremos una ecuación con una sola variable.
4. Resuelve la ecuación del paso 3 para la variable restante.
Resuelve la ecuación resultante del paso 3 para la variable restante. Si necesitas ayuda con esto, puedes mirar nuestra guía sobre cómo resolver ecuaciones con una incógnita.
5. Resuelve para la segunda variable.
Sustituye el valor que encontraste en el paso 4 en cualquiera de las dos ecuaciones y resuelve para la otra variable.
6. Verifica la solución en ambas ecuaciones.
Sustituye los valores de las incógnitas en ambas ecuaciones. Si es que ambas ecuaciones son verdaderas, los valores son la solución correcta.
EJEMPLO 1
Resuelve el sistema de ecuaciones usando el método de eliminación: $latex \begin{cases}2x+2y=10 \\ -2x+3y=5 \end{cases}$
Solución
Paso 1: Ambas ecuaciones ya están simplificadas y en la forma Ax+By=C.
Paso 2: Multiplica una o ambas ecuaciones por un número que creará coeficientes opuestos o bien para x o para y.
Ya tenemos coeficientes opuestos en la variable x.
Paso 3: Suma las ecuaciones.
$latex 2x+2y=10$
$latex + \hspace{1cm} -2x+3y=5$
______________________
$latex 5y=15$
Paso 4: Resuelve para la variable restante:
$latex 5y=15$
$latex y=3$
Paso 5: Resuelve para la segunda variable. Sustituímos $latex y=3$ en la primera ecuación:
$latex 2x+2y=10$
$latex 2x+2(3)=10$
$latex 2x+6=10$
$latex 2x=4$
$latex x=2$
Paso 6: Verifica la solución en ambas ecuaciones.
EJEMPLO 2
Resuelve el sistema de ecuaciones usando el método de eliminación: $latex \begin{cases}2x=y+3 \\ -x+3y=11 \end{cases}$
Solución
Paso 1: Ambas ecuaciones ya están simplificadas. Las colocamos en la forma Ax+By=C:
$latex \begin{cases}2x-y=3 \\ -x+3y=11 \end{cases}$
Paso 2: Multiplica una o ambas ecuaciones por un número que creará coeficientes opuestos o bien para x o para y.
Multiplicamos la segunda ecuación por 2:
$latex \begin{cases}2x-y=3 \\ -2x+6y=22 \end{cases}$
Paso 3: Suma las ecuaciones.
$latex 2x-y=3$
$latex + \hspace{1cm} -2x+6y=22$
___________________
$latex 5y=25$
Paso 4: Resuelve para la variable restante:
$latex 5y=25$
$latex y=5$
Paso 5: Resuelve para la segunda variable. Sustituimos $latex y=5$ en la primera ecuación:
$latex 2x-y=3$
$latex 2x-5=3$
$latex 2x=8$
$latex x=4$
Paso 6: Verifica la solución en ambas ecuaciones.
Inténtalo tú mismo – Resuelve los ejercicios
Véase también
¿Interesado en aprender más sobre ecuaciones? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
