Existen tres métodos básicos para graficar funciones lineales. El primero consiste en graficar puntos y luego trazar una recta para unir los puntos. El segundo método consiste en usar el intercepto en y y la pendiente. El tercero método consiste en aplicar transformaciones a la función $latex f(x)=x$.
A continuación, aprenderemos cómo graficar funciones lineales usando los tres métodos mencionados. Además, veremos algunos ejemplos de práctica.
Gráficar funciones lineales usando puntos
Podemos usar diferentes valores de entradas y evaluar a la función con esos valores para obtener diferentes coordenadas cartesianas. Luego, graficamos estos puntos en un plano cartesiano. Debemos evaluar la función con al menos dos valores de entrada diferentes para obtener al menos dos puntos diferentes para poder graficar la función.
Por ejemplo, si es que tenemos la función $latex f(x)=x+2$, podemos usar los valores de entrada 1 y 2. Al evaluar la función con el valor de entrada 1, obtenemos el valor de salida 3, lo cual forma el punto con coordenadas cartesianas (1, 3). Usando el valor de entrada 2, obtenemos el valor de salida 4, formando el punto con coordenadas (2, 4).
Para evitar cometer errores, podemos usar tres puntos. De este modo, si es que la línea no pasa a través de los tres puntos, sabemos que cometimos algún error.
¿Cómo graficar una función lineal usando puntos?
Paso 1: Escoge un mínimo de dos valores de entrada.
Paso 2: Evalúa la función en cada valor de entrada.
Paso 3: Usa los valores de salida resultantes para formar coordenadas cartesianas.
Paso 4: Grafica las coordenadas cartesianas en una cuadrícula.
Paso 5: Traza una línea a través de los puntos.
EJEMPLO 1
Grafica la función $latex f(x)=2x-3$ usando puntos.
Solución: Empezamos escogiendo los valores de entradas. Vamos a escoger tres valores diferentes. Escogeremos el -2, 0 y 2.
Evalúa la función en cada valor de entrada y usa el valor de salida para formar las coordenadas cartesianas de los puntos:
$latex x=-2$ $latex f(-2)=2(-2)-3=-7$ ⇒$latex (-2, -7)$
$latex x=0$ $latex f(0)=2(0)-3=-3$ ⇒$latex (0, -3)$
$latex x=2$ $latex f(2)=2(2)-3=1$ ⇒$latex (2, 1)$
Graficamos los puntos y trazamos una línea que pase a través de esos puntos. La siguiente es la gráfica de $latex f(x)=2x-3$:
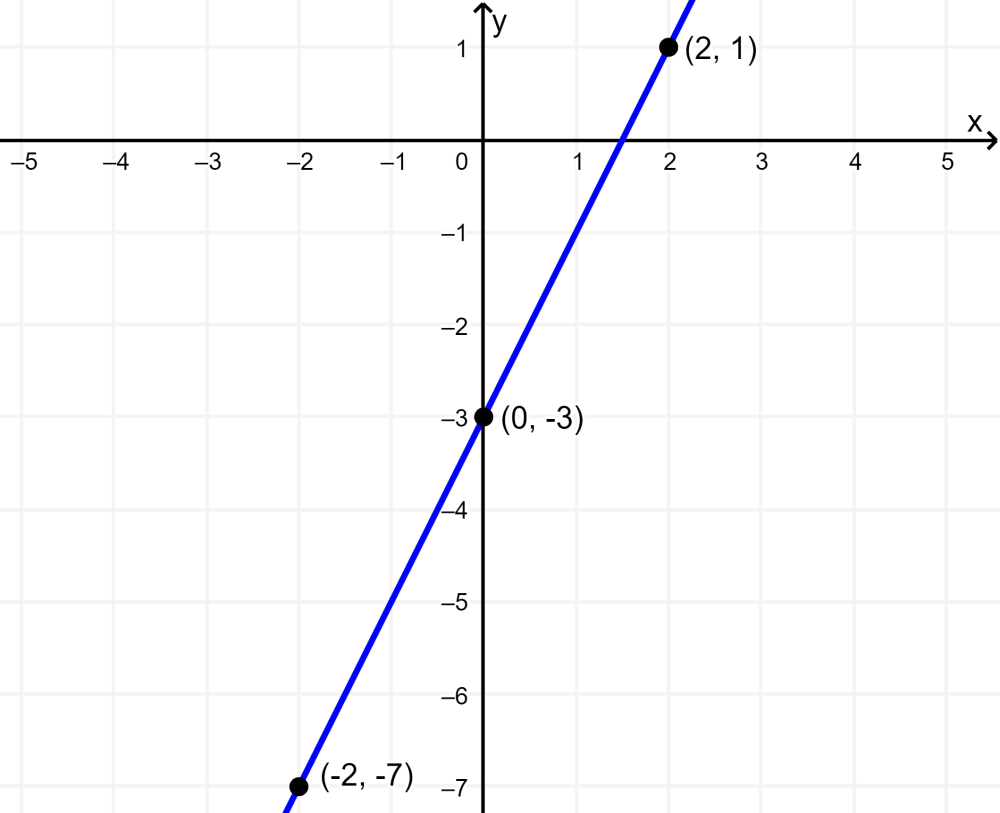
Podemos ver que como esperábamos, la gráfica de la función es una línea recta. Esta línea tiene una inclinación hacia arriba lo que indica una pendiente positiva.
EJEMPLO 2
Grafica la función $latex f(x)=-\frac{1}{3}x+4$ usando puntos.
Solución: Empezamos escogiendo los valores de entradas. Ahora tenemos una fracción, por lo que podemos escoger múltiplos del 3 o el 0 para facilitar el problema. Vamos a escoger tres números diferentes. Escogeremos el -3, 0 y 3.
Usamos cada uno de los valores de entrada para obtener valores de salida y formamos las coordenadas cartesianas de los puntos:
$latex x=-3$ $latex f(-3)=-\frac{1}{3}(-3)+4=5$ ⇒$latex (-3, 5)$
$latex x=0$ $latex f(0)=-\frac{1}{3}(0)+4=4$ ⇒$latex (0, 4)$
$latex x=3$ $latex f(3)=-\frac{1}{3}(3)+4=3$ ⇒$latex (3, 3)$
Colocamos esos puntos en el plano cartesiano y trazamos una línea que pase a través de esos puntos. La siguiente es la gráfica de $latex f(x)=-\frac{1}{3}x+4$:
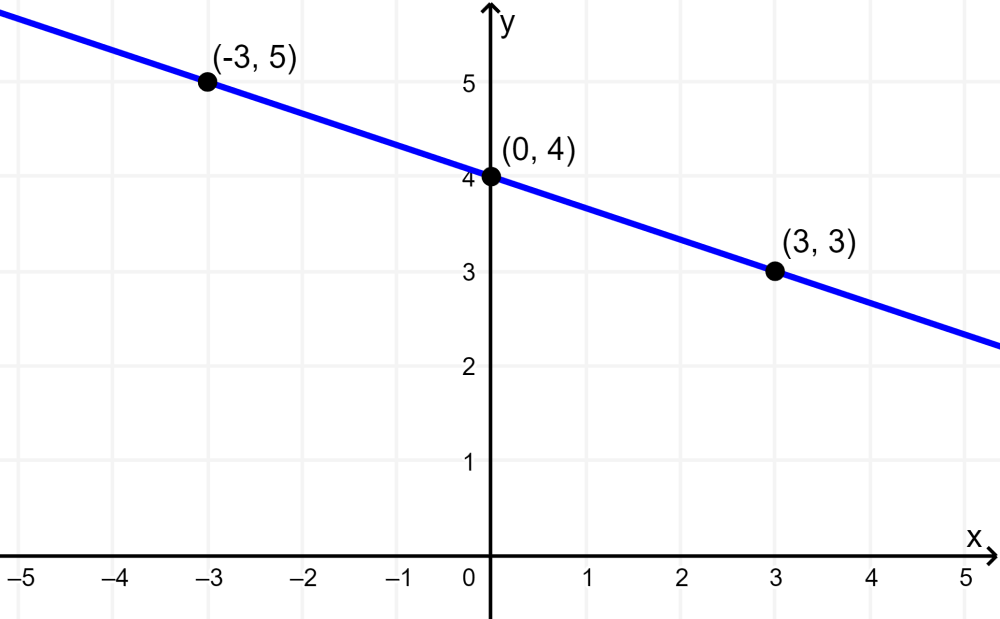
Nuevamente, vemos que la gráfica de la función es una línea recta. Esta línea tiene una inclinación hacia abajo lo que indica una pendiente negativa.
Gráficar funciones lineales usando la pendiente y el intercepto en y
En vez de usar puntos, otra forma de graficar funciones lineales es usando las características principales de las funciones lineales. La primera característica es el intercepto en y, el cual es el punto cuando el valor de x es 0. Para encontrar el intercepto en y, simplemente usamos el valor $latex x=0$ en la función.
La otra característica de la función lineal es su pendiente, m, la cual es una medida de la inclinación de la línea. La pendiente en una función lineal es igual a la tasa de variación en los valores de salida sobre la tasa de variación de los valores de entrada. Es decir, la pendiente es el cambio en los valores de y sobre el cambio en los valores de x.
Encontramos la pendiente y el intercepto en y de las funciones lineales. Vamos a usar estas características para graficar estas funciones. Miremos la siguiente función:
$latex f(x)=2x-5$
La pendiente es 2. Dado que la pendiente es positiva, sabemos que la línea tendrá una inclinación hacia arriba, es decir, crece de izquierda a derecha. El intercepto en y es el punto en la gráfica cuando $latex x=0$. Entonces, la gráfica cruza al eje y en el punto (0, -5).
Ahora que sabemos la pendiente y el intercepto en y, podemos empezar graficando el punto (0, -5). Sabemos que la pendiente es cambio en y sobre cambio en x. Aquí tenemos $latex m=2$, lo que significa que el cambio en y es 2 y el cambio en x es 1.
Empezando del punto (0, -5), podemos avanzar 1 en x y 2 en y. Repetimos hasta que tengamos varios puntos y trazamos una línea.
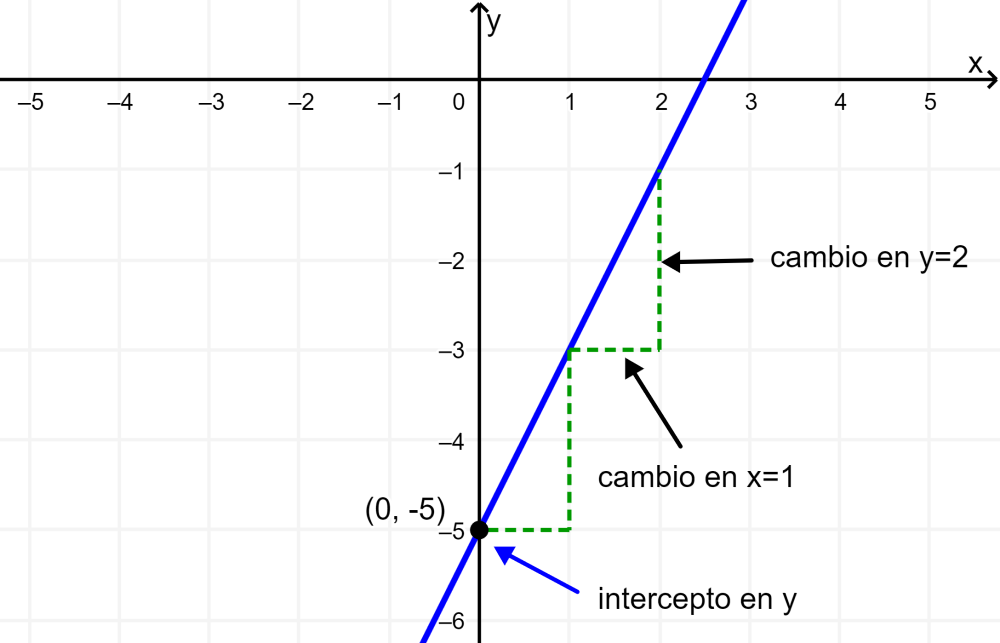
¿Cómo graficar funciones lineales usando la pendiente y el intercepto en y?
Paso 1: Evalúa la función con $latex x=0$ para encontrar el intercepto en y.
Paso 2: Identifica la pendiente.
Paso 3: Grafica el punto que representa al intercepto en y.
Paso 4: Identifica más puntos en la línea usando el cambio en y sobre el cambio en x.
Paso 5: Traza la línea que pasa a través de los puntos.
EJEMPLO 1
Grafica la función $latex f(x)=3x-3$ usando la pendiente y el intercepto en y.
Solución: Evalúa la función en el punto $latex x=0$ para encontrar el intercepto en y. El valor de la función cuando $latex x=0$ es -3, por lo que la gráfica cruza al eje y en el punto (0, -3). La pendiente de la línea es 3.
Esto nos dice que, cada vez que nos movemos 1 unidad en el eje x, nos movemos 3 unidades en el eje y. Luego de marcar varios puntos, trazamos una línea a través de esos puntos:
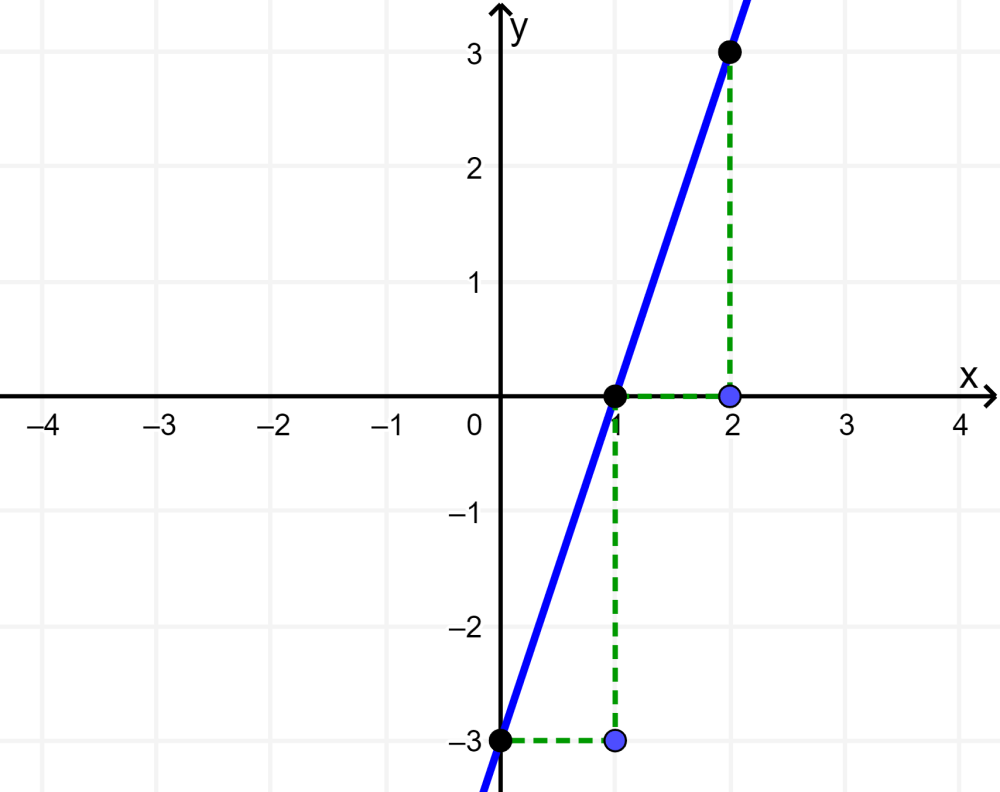
Podemos ver que la gráfica incrementa de izquierda a derecha, por lo que tiene una pendiente positiva tal como esperábamos.
EJEMPLO 2
Grafica la función $latex f(x)=-\frac{1}{2}x+5$ usando la pendiente y el intercepto en y.
Solución: Evaluamos la función en el punto $latex x=0$ para encontrar el intercepto en y. Cuando tenemos $latex x=0$, el valor de la función es 5, por lo que el punto de intersección es (0, -3). Vemos que la pendiente de la línea es $latex -\frac{1}{2}$.
Esto significa que, cada vez que nos movemos 2 unidades en el eje x, nos movemos -1 unidades en el eje y. Marcamos varios puntos y trazamos una línea que cruce a esos puntos:
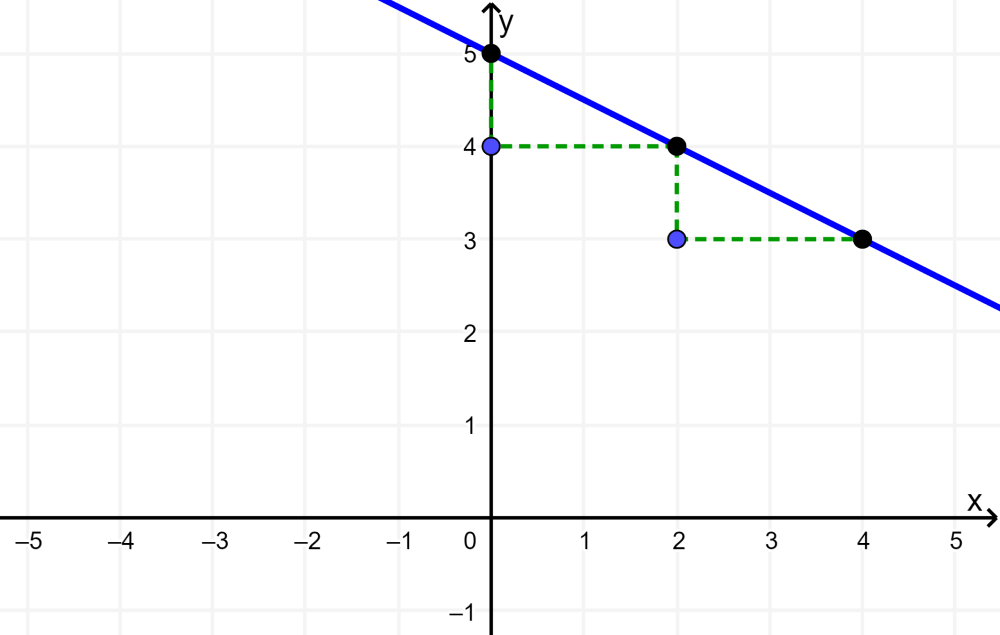
En esta ocasión, la gráfica decrece de izquierda a derecha, lo que significa que la pendiente es negativa.
Gráficar funciones lineales usando transformaciones
Otra forma de graficar funciones es usando transformaciones en la función identidad $latex f(x)=x$. Una función puede ser transformada al trasladarla hacia arriba, hacia abajo, hacia la izquierda o hacia la derecha. También podemos transformar una función al estirarla, encogerla o reflejarla.
Compresión o estiramiento vertical
En la ecuación $latex f(x)=mx$, la m está actuando como la compresión o el estiramiento vertical de la función. Cuando m es negativa, también tenemos una reflexión de la función con respecto al eje x. Entre más grande sea el valor de m, más inclinada será la línea:
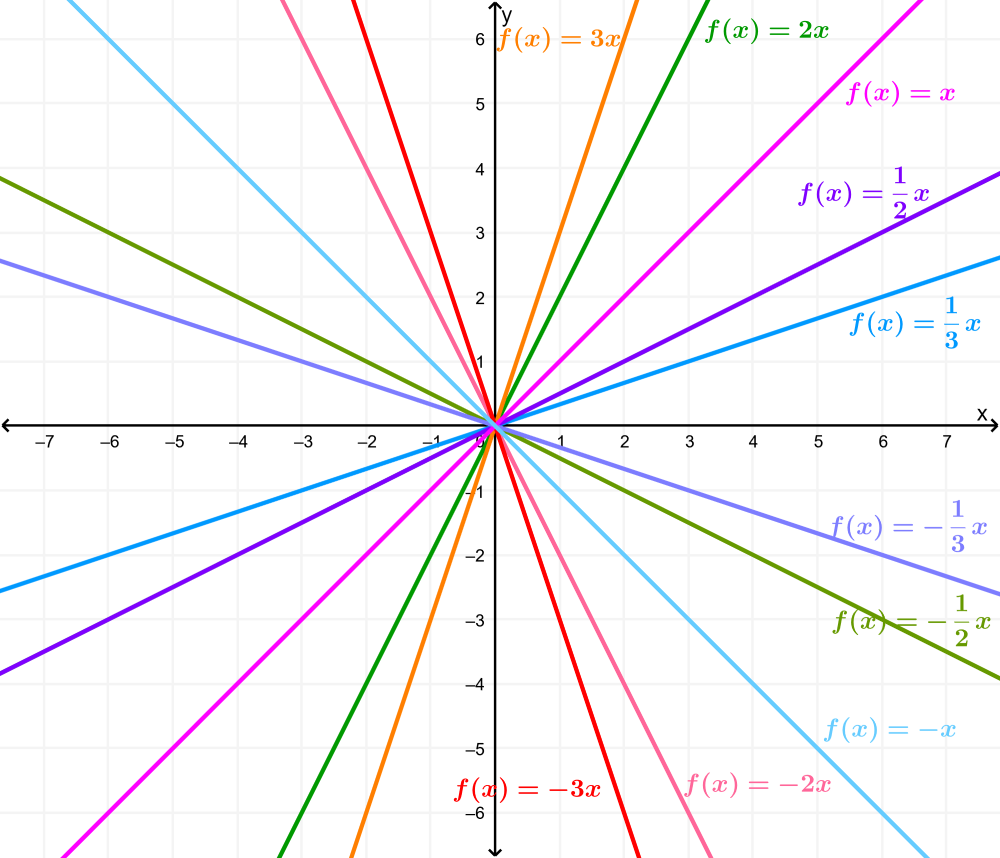
Traslación vertical
Cuando tenemos $latex f(x)=mx+b$, la b actúa como la traslación vertical, la cuál mueve la gráfica hacia arriba o hacia abajo sin afectar a la pendiente. Si es que b es positivo, la gráfica es trasladada b unidades hacia arriba y si es que b es negativo, la gráfica es trasladada b unidades hacia abajo.
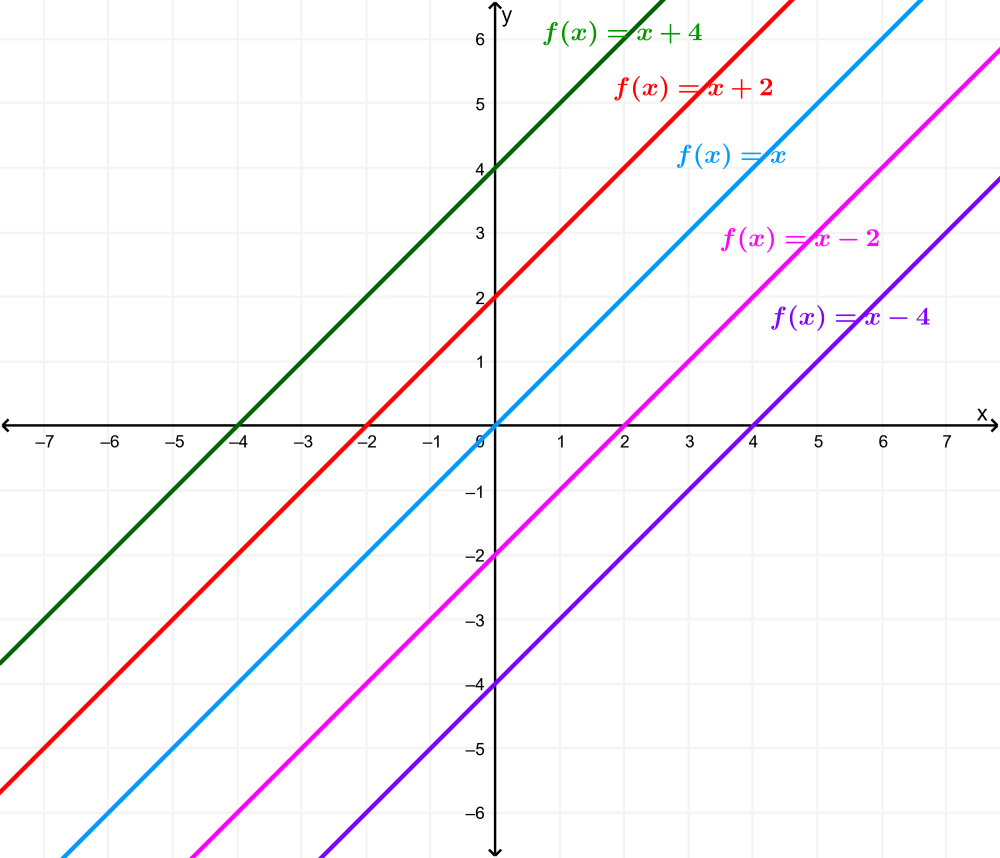
¿Cómo graficar funciones lineales usando transformaciones?
Paso 1: Grafica la función $latex f(x)=x$.
Paso 2: Estira o encoge la gráfica verticalmente por un factor m.
Paso 3: Traslada la gráfica hacia arriba o hacia abajo por b unidades.
EJEMPLO 1
Grafica la función $latex f(x)=4x-2$ usando transformaciones.
Solución: La ecuación de la función muestra que $latex m=4$, por lo que la gráfica es estirada verticalmente por 4. La ecuación de la función también muestra que $latex b=-2$, por lo que la gráfica es trasladada hacia abajo por 2 unidades.
Primero, graficamos la función identidad y aplicamos el estiramiento vertical:
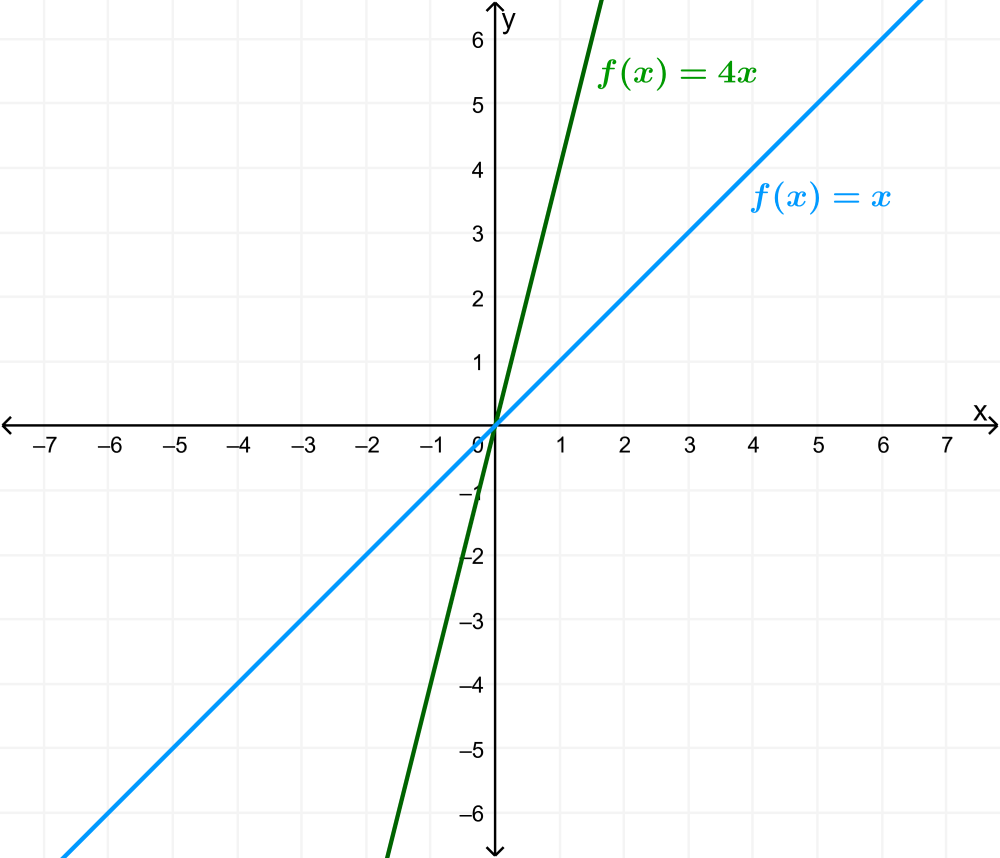
Luego, aplicamos la traslación vertical:
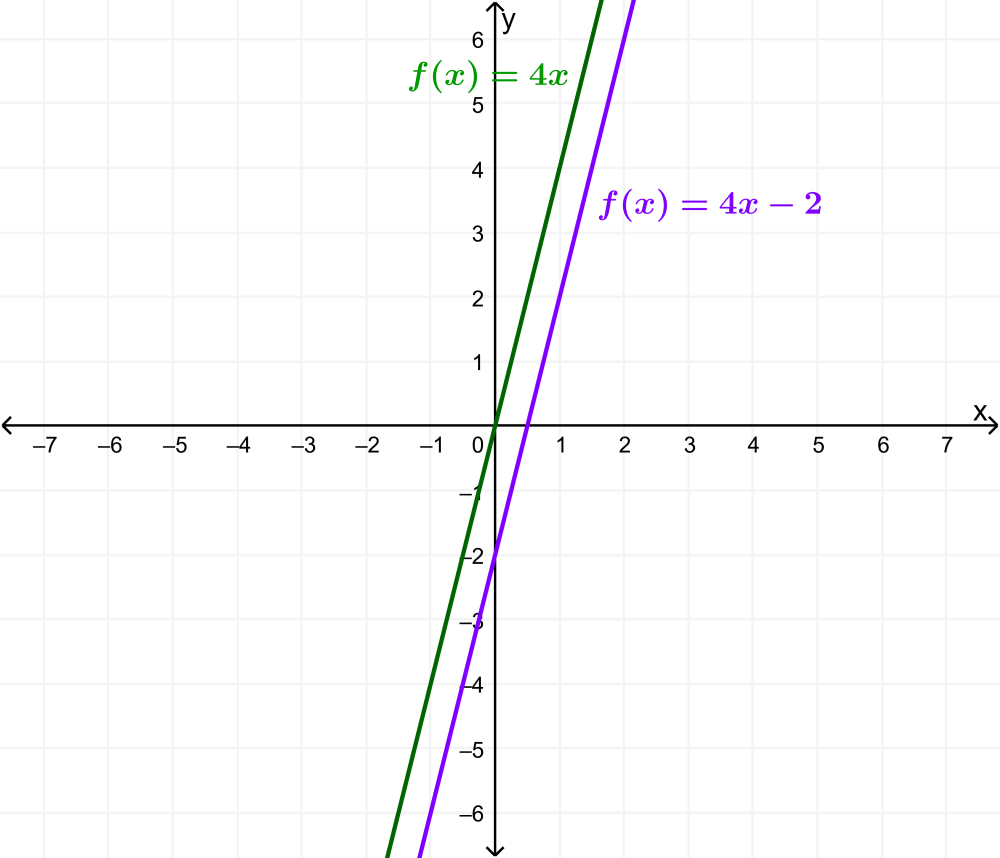
EJEMPLO 2
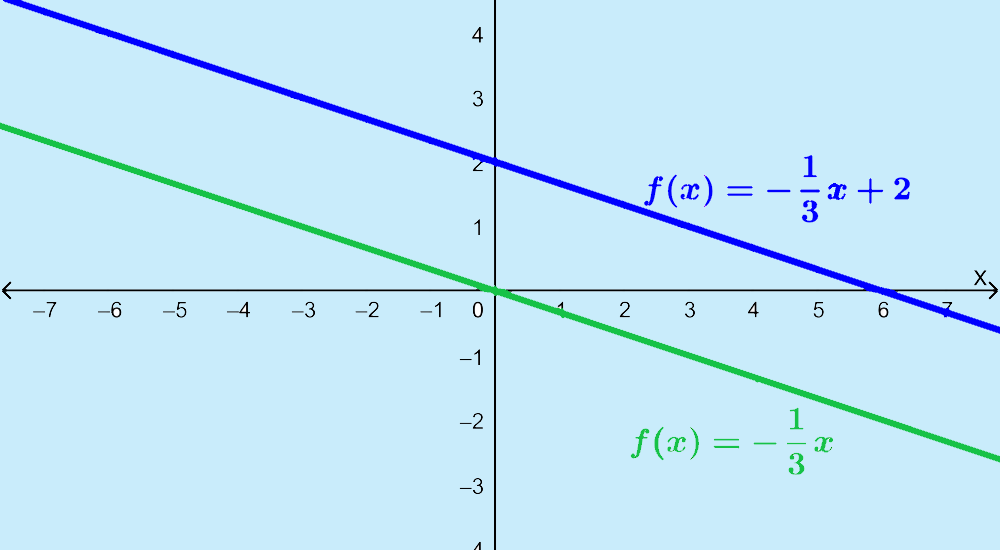
Grafica la función $latex f(x)=-\frac{1}{3}x+2$ usando transformaciones.
Solución: Podemos ver que $latex m=-\frac{1}{3}$, por lo que la gráfica es encogida verticalmente por $latex \frac{1}{3}$. También podemos ver que $latex b=2$, por lo que la tenemos que trasladar la gráfica hacia arriba por 2 unidades.
Primero, graficamos la función identidad y aplicamos la compresión vertical:
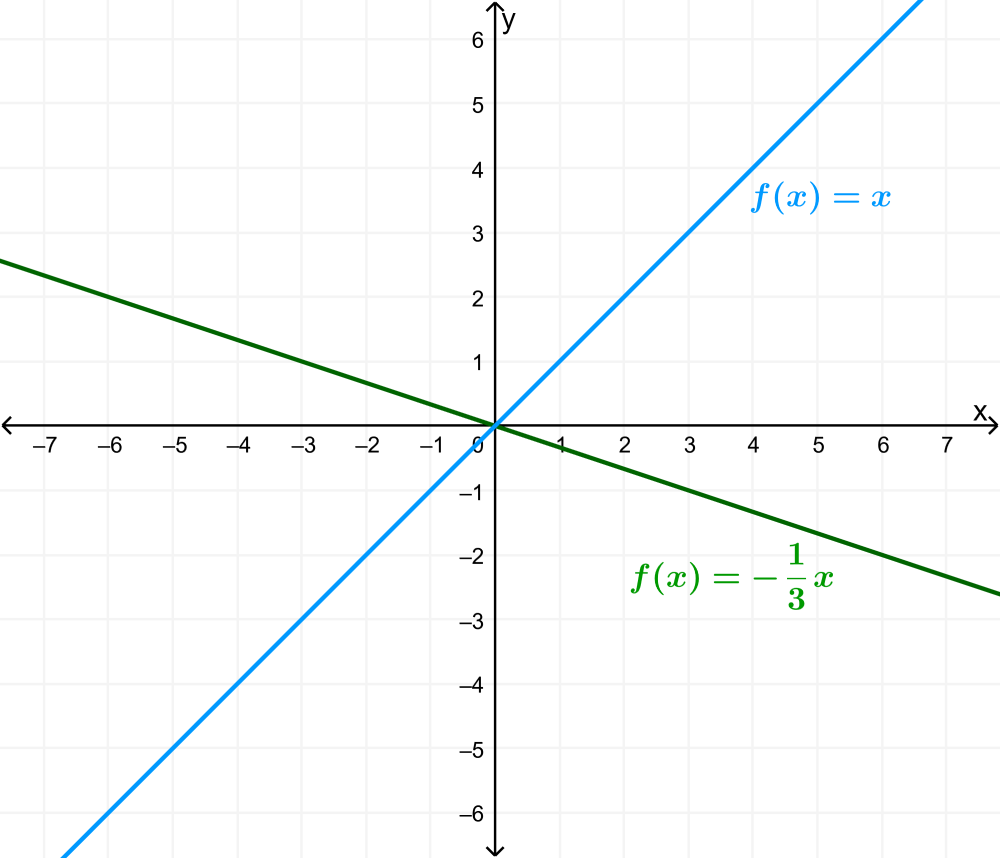
Luego, aplicamos la traslación vertical:
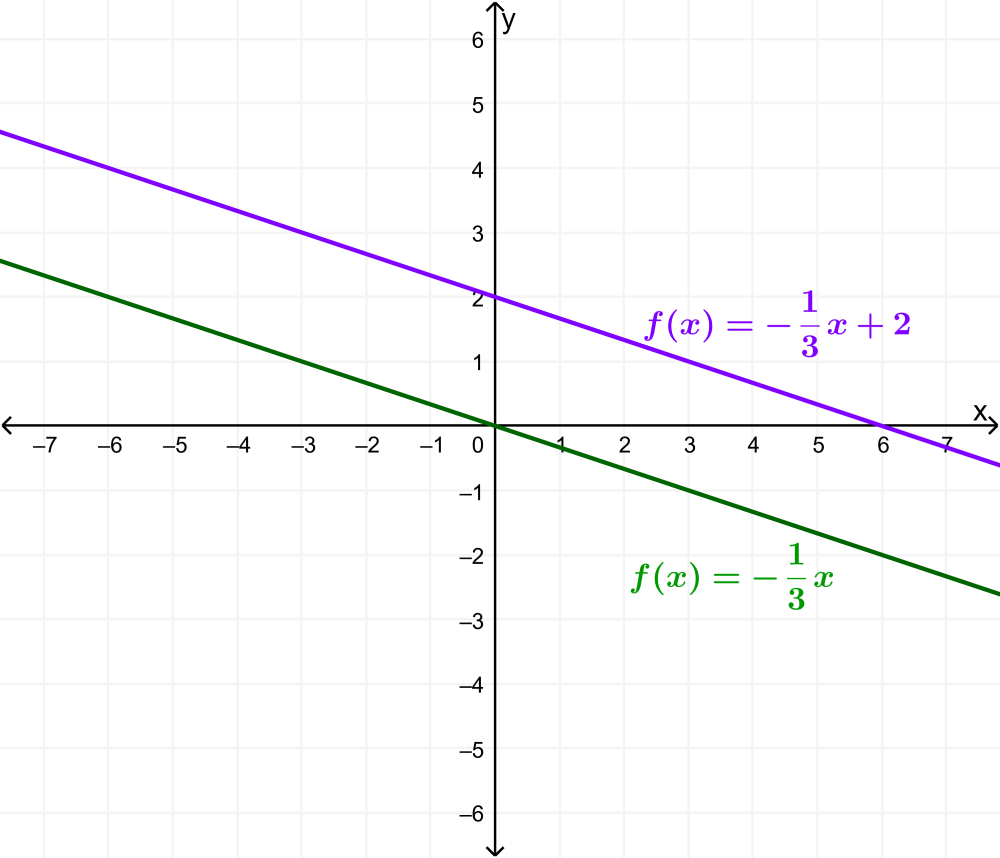
Véase también
¿Interesado en aprender más sobre gráficas de funciones? Mira estas páginas: