Seno, coseno y tangente son las funciones trigonométricas más importantes. Para obtener las gráficas de funciones trigonométricas necesitamos conocer el periodo, la fase y la amplitud. Las gráficas de cosecante, secante y cotangente se obtienen considerando que son funciones recíprocas de seno, coseno y tangente respectivamente.
En este artículo, aprenderemos sobre las representaciones gráficas de las funciones seno, coseno y tangente. También aprenderemos sobre la amplitud, la fase y el periodo de estas funciones.
Gráfica del seno
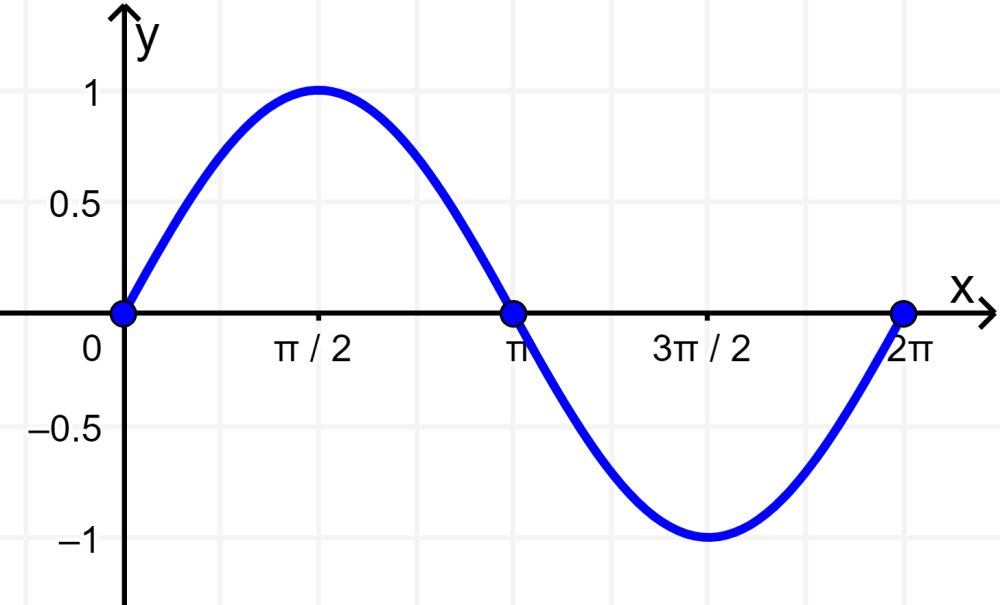
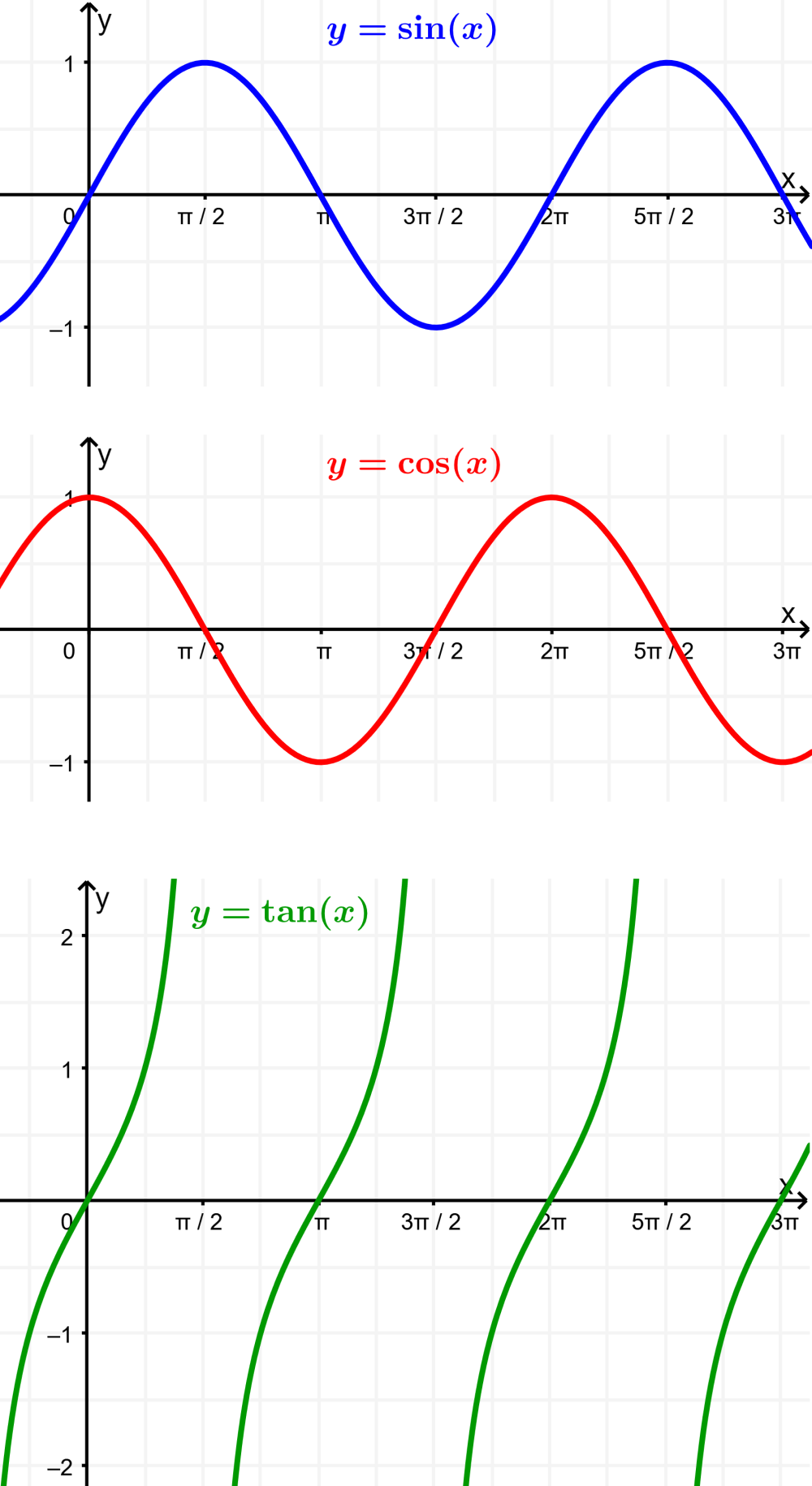
La función seno es una de las funciones trigonométricas fundamentales. Podemos escribir $latex y=\sin (x)$ o $latex f(x)=\sin (x)$. La siguiente es la gráfica de del seno:
La función seno tiene las siguientes características:
- Las raíces o los ceros de $latex y=\sin (x)$ son los múltiplos de π.
- La gráfica del seno pasa a través del origen, ya que cuando x es 0, tenemos $latex \sin (0)=0$.
- El periodo de la función seno es 2π.
- La altura de curva en cada punto es igual a el valor de la función seno en cada punto.
- El valor máximo de la función es 1 cuando $latex x=\frac{\pi }{2}$.
- El valor mínimo de la función es -1 cuando $latex x=\frac{3\pi }{2}$.
Gráfica del coseno
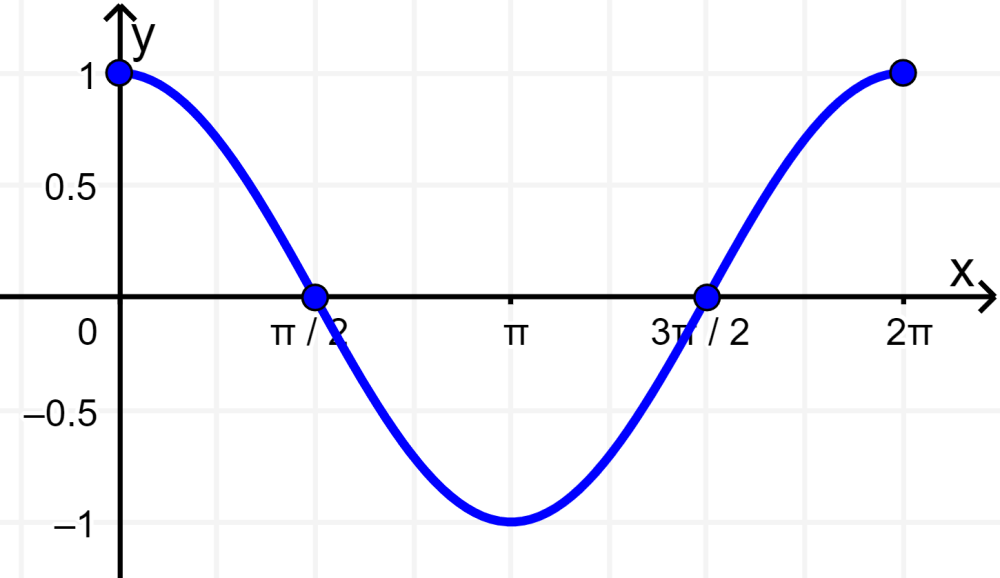
Para el coseno, podemos escribir $latex y=\cos (x)$ o $latex f(x)=\cos (x)$. La siguiente es la gráfica de del coseno:
Las siguientes son las características de la gráfica de la función coseno:
- Tenemos esta identidad $latex \sin\left( {x+\frac{\pi }{2}} \right)=\cos \left( x \right)$.
- La gráfica del coseno es la gráfica que obtenemos si es que trasladamos a la gráfica de seno $latex \frac{\pi }{2}$ unidades hacia la izquierda.
- Las raíces o los ceros de la función coseno son los múltiplos de π/2.
- La gráfica del seno cruza al eje y en el punto (0, 1).
- El periodo de la función coseno es 2π.
- El valor máximo de la función es 1 cuando $latex x=0$.
- El valor mínimo de la función es -1 cuando x es π.
Podemos observar las siguientes similitudes entre las gráficas de seno y las gráficas de coseno:
- Ambas producen la misma curva, la cual es trasladada a lo largo del eje x.
- Ambas tienen una amplitud de 1.
- Ambas tienen un periodo de 2π o de 360°.
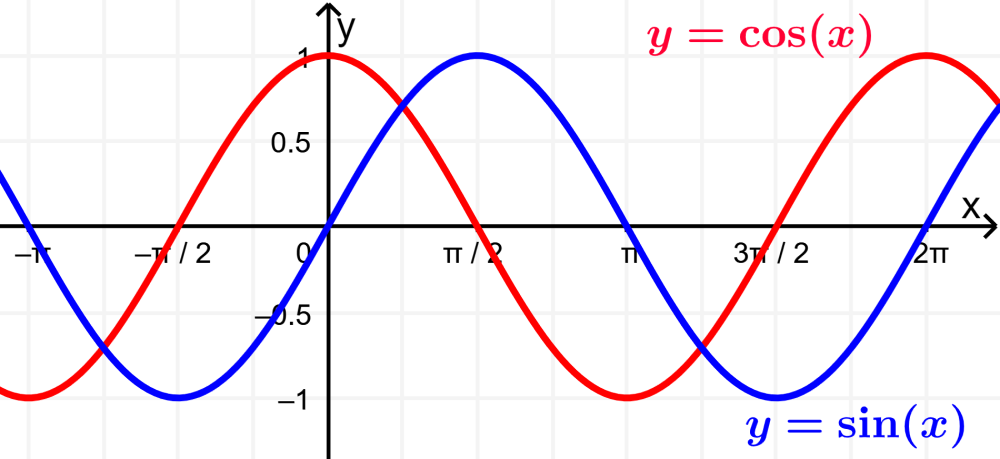
La siguiente gráfica nos muestra una comparación de las funciones seno y coseno:
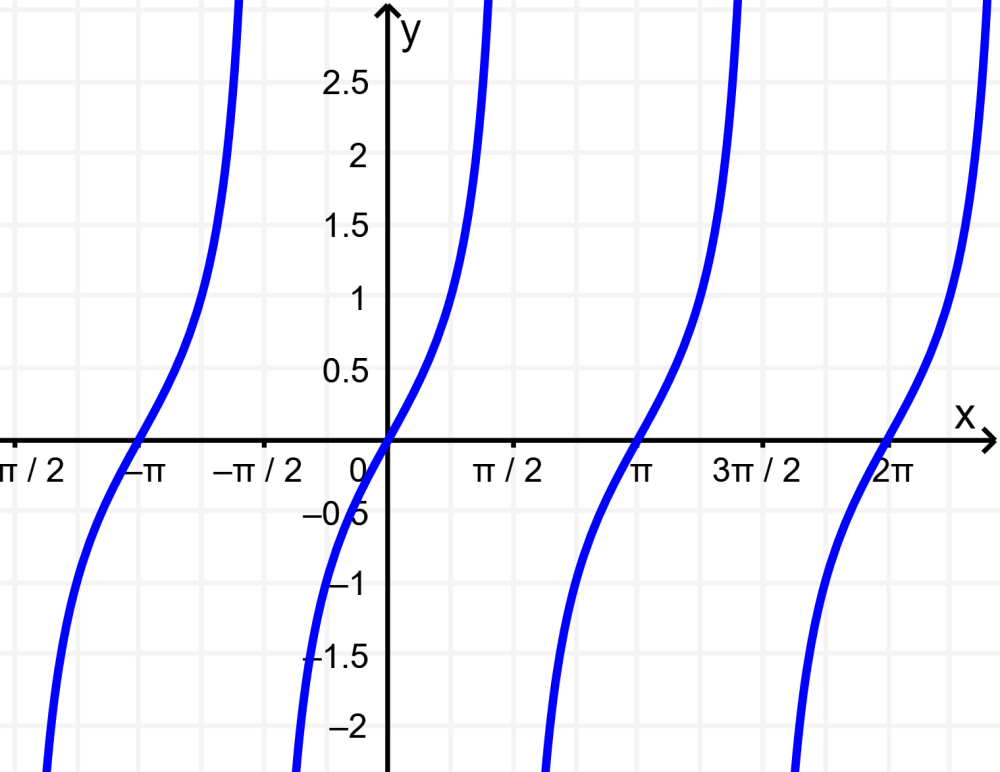
Gráfica de la tangente
La gráfica de la tangente es completamente diferente en comparación con la gráfica del seno y del coseno. La gráfica de la función tangente tiene valores que van desde negativo infinito hasta positivo infinito y cruza al eje x sobre un periodo de π radianes:
Las siguientes son las características de la función tangente:
- Las raíces o los ceros de la función son los múltiplos de π.
- La gráfica de la tangente pasa a través del origen.
- La gráfica de la tangente tiene una amplitud indefinida debido a que la curva tiende a infinito.
- El periodo de la función seno es π o 180°.
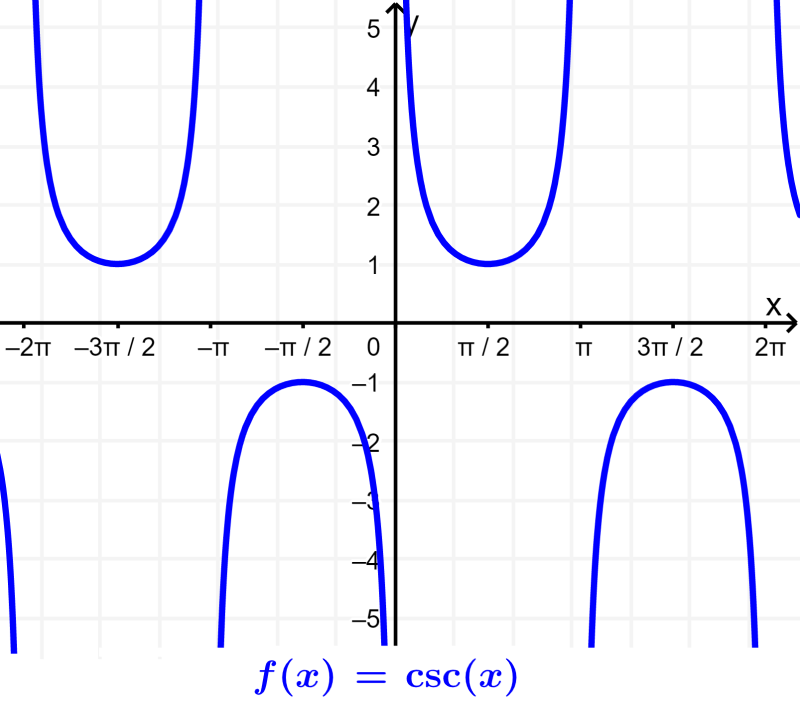
Gráfica de la cosecante
La cosecante es la función recíproca del seno. Esto significa que la función cosecante es obtenida al dividir a 1 por el seno. Entonces, la función cosecante resulta en indefinido cuando el seno es igual a 0 (múltiplos de π).
Las siguientes son algunas características importantes de la función cosecante:
- La cosecante no tiene raíces o ceros. Podemos ver que la gráfica no toca al eje x.
- La cosecante es indefinida en los múltiplos de π. Es decir, tiene asíntotas en estos puntos.
- El rango de la función cosecante es todos los números reales a excepción de -1<y<1.
- La gráfica de la cosecante tiene una amplitud indefinida.
- El periodo de la función cosecante es 2π o 360°.
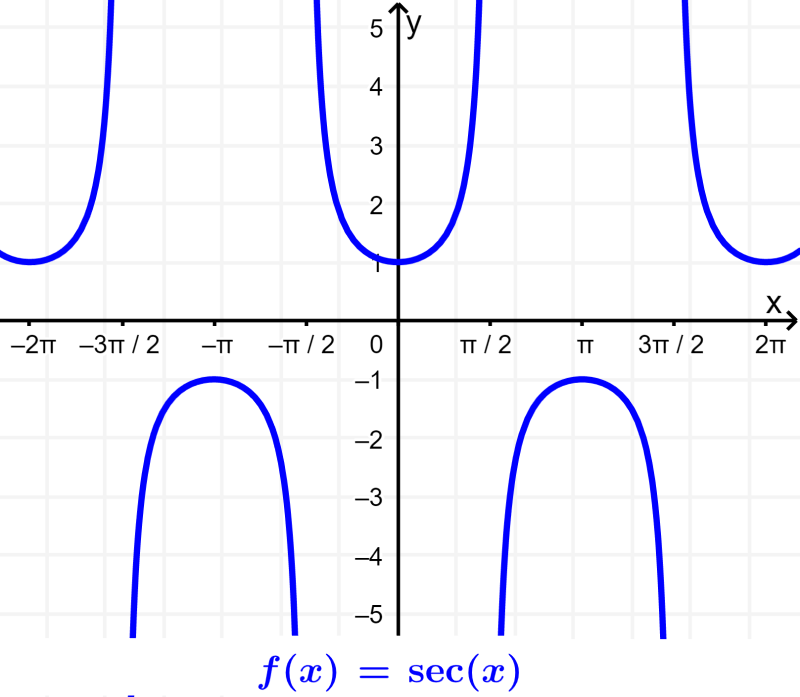
Gráfica de la secante
La secante es la función recíproca del coseno. Es decir, podemos obtener a la función secante al dividir a 1 por el coseno. Entonces, la función secante resulta en indefinido cuando el coseno es igual a 0 (π/2±nπ, en donde n es un número entero).
Las siguientes son algunas características importantes de la función secante:
- La función secante nunca toca al eje x. Esto significa que no tiene raíces o ceros.
- La secante tiene asíntotas en los múltiplos de π/2, ya que es indefinida en estos puntos.
- El rango de la función secante es todos los números reales a excepción de -1<y<1.
- La secante tiene una amplitud indefinida.
- El periodo de la función secante es 2π o 360°.
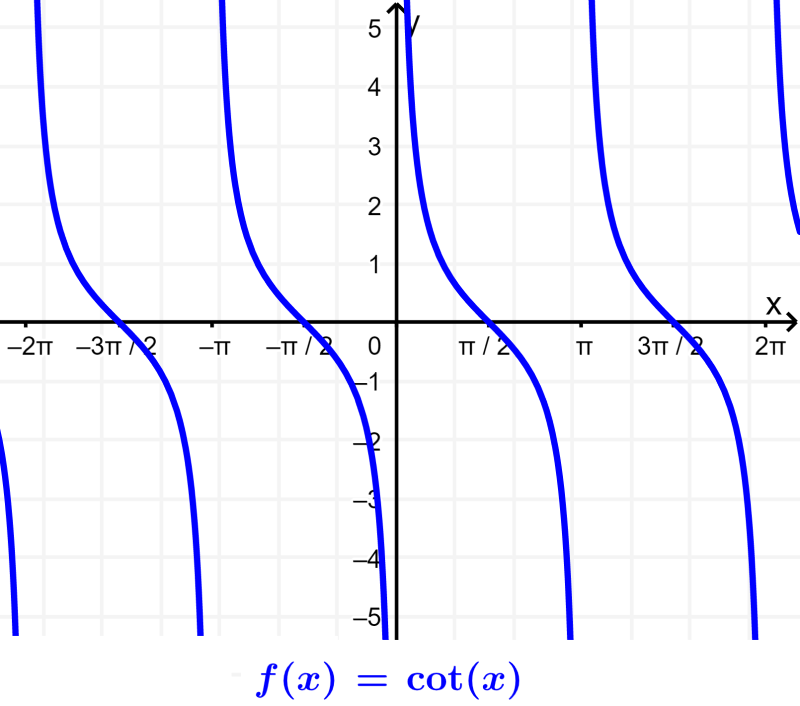
Gráfica de la cotangente
La cotangente es la función recíproca de la tangente. Es decir, la cotangente es equivalente a 1 sobre la función tangente. Entonces, la función cotangente resulta en indefinido cuando la tangente es igual a 0 (múltiplos de π).
Las siguientes son algunas características importantes de la función cotangente:
- Los ceros o raíces de la cotangente están ubicamos en π/2±nπ, en donde n es un número entero.
- La cotangente es indefinida en los múltiplos de π. Es decir, tiene asíntotas en estos puntos.
- El rango de la cotangente es todos los números reales.
- La gráfica de la cotangente tiene una amplitud indefinida.
- El periodo de la función cotangente es π o 180°.
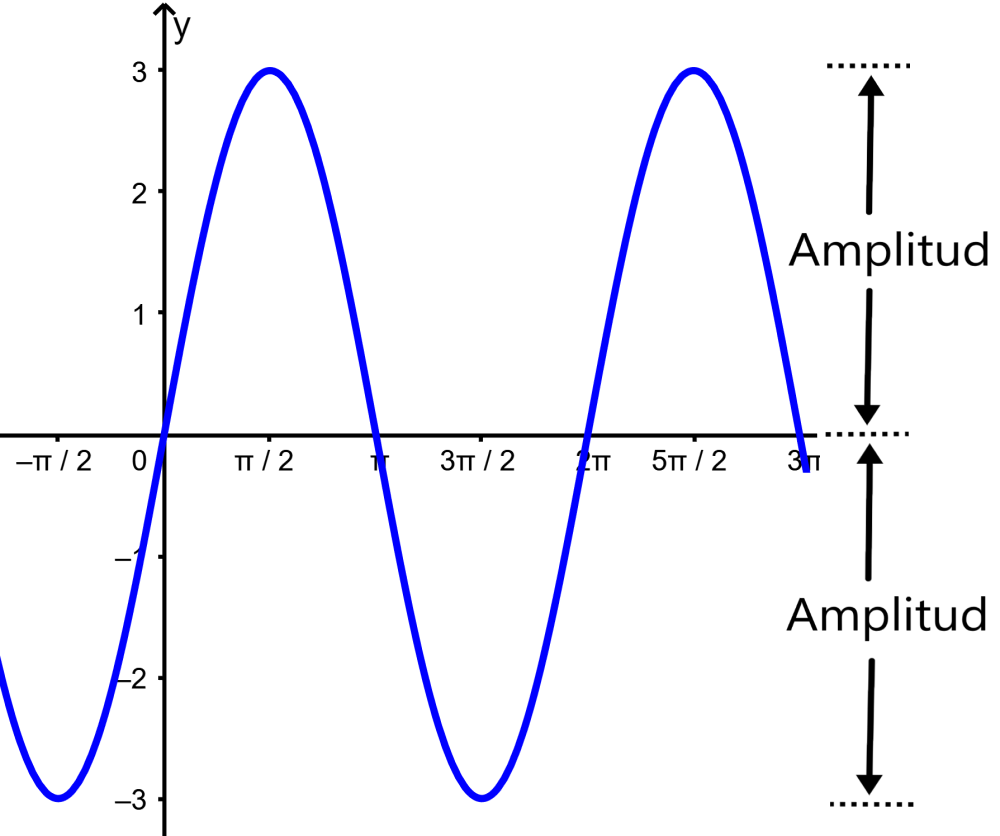
Amplitud
La amplitud es la altura desde la línea central de una función trigonométrica hasta su punto máximo o su punto mínimo. La amplitud es el valor absoluto por el que una función trigonométrica es multiplicada.
La amplitud también puede ser medida al tomar la altura del punto más alto desde el punto más bajo y dividir para 2. La amplitud nos indica qué tan alta o tan baja es la gráfica de una función trigonométrica.
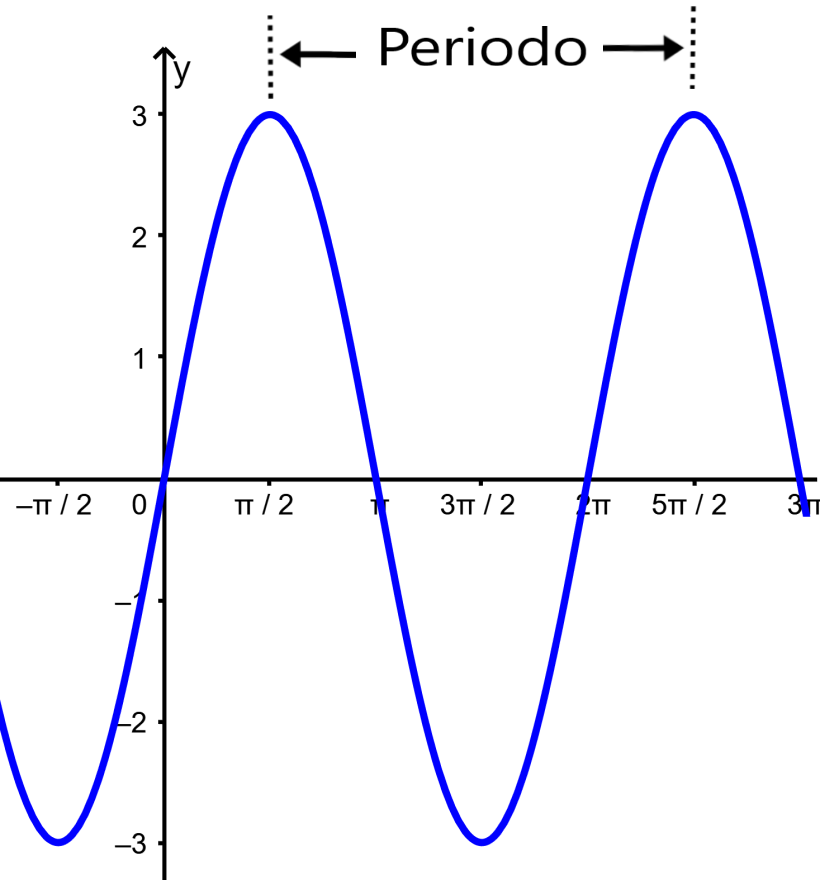
Periodo
El periodo es la medida desde un punto en la gráfica, por ejemplo, un punto máximo, hasta el siguiente punto equivalente. La siguiente es una representación gráfica del periodo de la función seno:
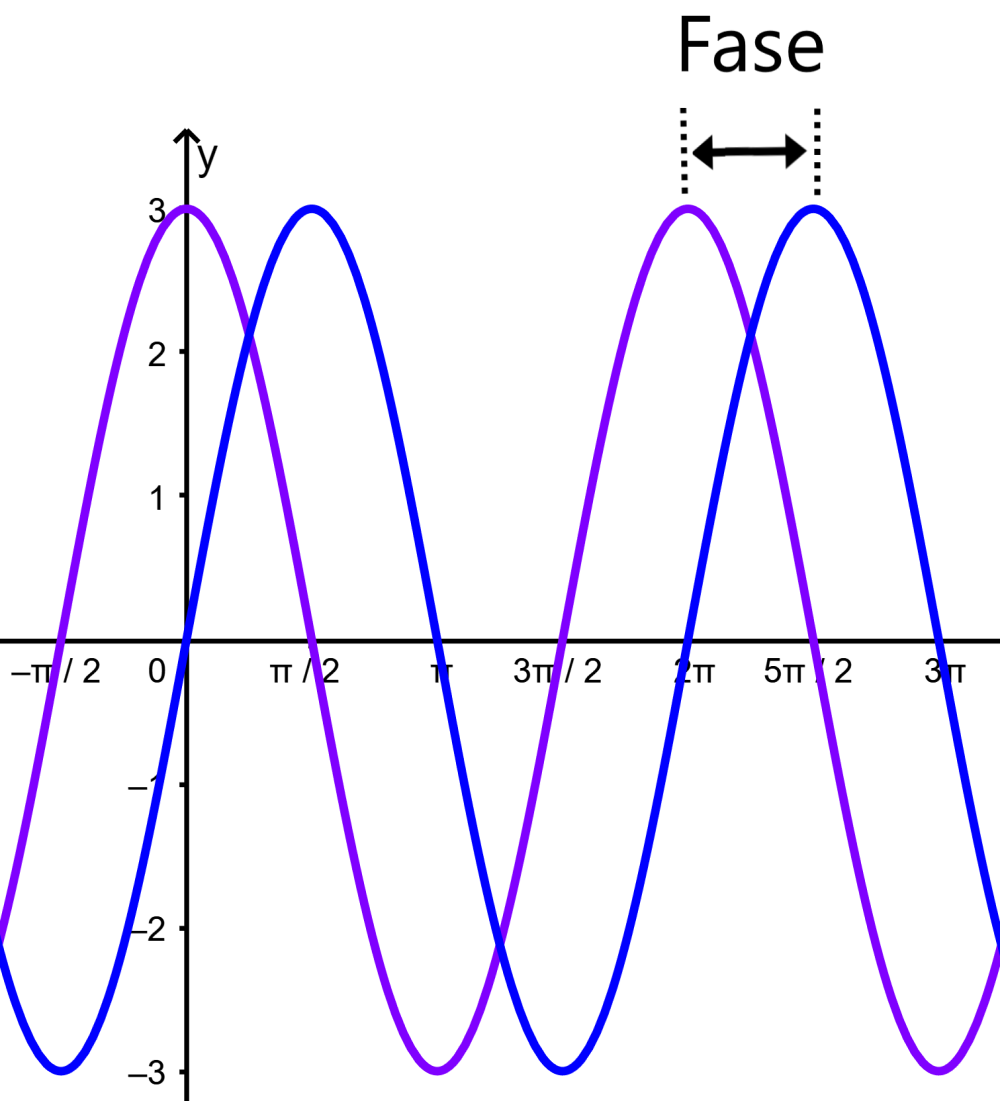
Fase
La fase es una medida de la traslación horizontal de una función trigonométrica desde su posición original. La siguiente es una representación gráfica de la fase de la función seno:
¿Cómo trazar gráficas de funciones trigonométricas?
Existen varios métodos que pueden ser usados para graficar funciones trigonométricas. La siguiente es una explicación detallada de uno de los métodos más eficientes para graficar funciones trigonométricas.
Para trazar la gráfica de funciones trigonométricas, debemos empezar convirtiendo la función dada a la forma general $latex a\sin(bx-c)+d$. En esta forma, podremos encontrar fácilmente los diferentes parámetros como amplitud, fase, periodo y traslación vertical, en donde:
- $latex |a|=$ amplitud
- $latex \frac{{2\pi }}{|b|}=$ periodo
- $latex \frac{{c }}{b}=$ fase
- $latex d=$ traslación vertical
De igual forma, podemos encontrar la gráfica del coseno usando la forma $latex a\cos(bx-c)+d$.
Las gráficas de las funciones trigonométricas fundamentales están mostradas abajo en su forma base:
EJEMPLO 1
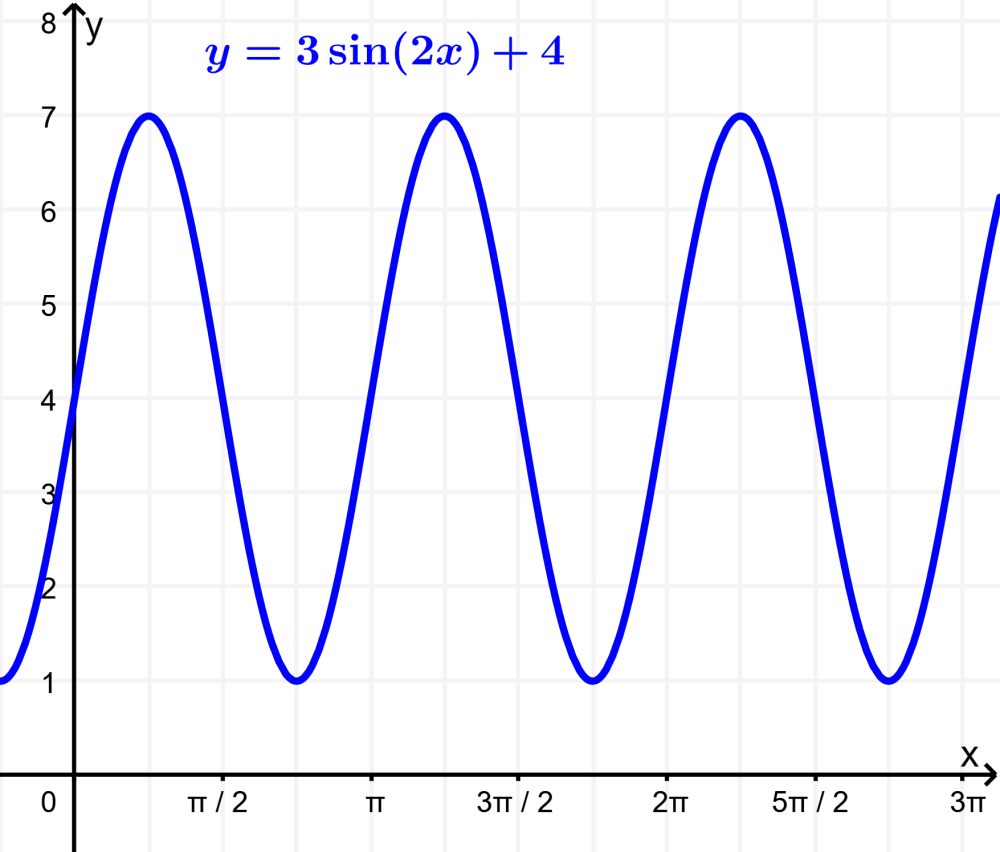
Traza la gráfica de la función $latex y=3\sin \left( {2x} \right)+4$.
Solución:
- La amplitud es 3, por lo que la distancia entre los valores mínimos y los valores máximos es 6.
- El número de ondas es 2. Cada onda tiene un periodo de 360°÷2=180°.
- La gráfica es trasladada hacia arriba por 4 unidades.
- El punto máximo es (3×1)+4=7 y el punto mínimo es (3×-1)+4=1.
- El periodo es $latex \frac{{2\pi }}{2}=\pi $
La gráfica se ve de la siguiente manera:
EJEMPLO 2
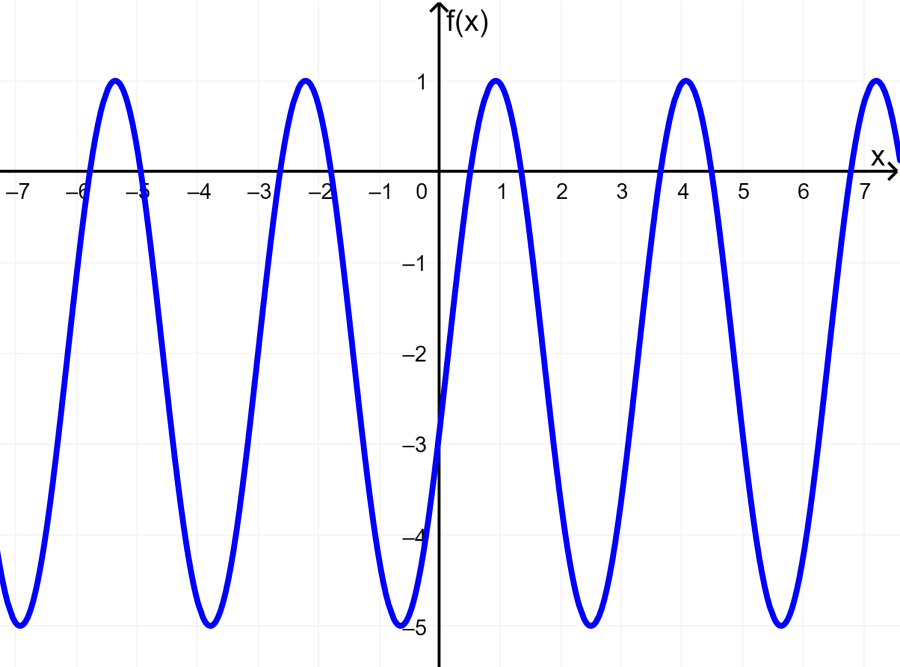
- La siguiente es la gráfica de la función $latex y=3\sin(2(x+3))-2$.
En esta función, tenemos:
- Amplitud: $latex A=2$
- Periodo: $latex \text{periodo}=\frac{2\pi}{B}=\frac{2\pi}{2}=\pi$
- Fase: $latex C=-3$
- Traslación vertical: $latex D=-2$
Véase también
¿Interesado en aprender más sobre gráficas de funciones? Mira estas páginas: