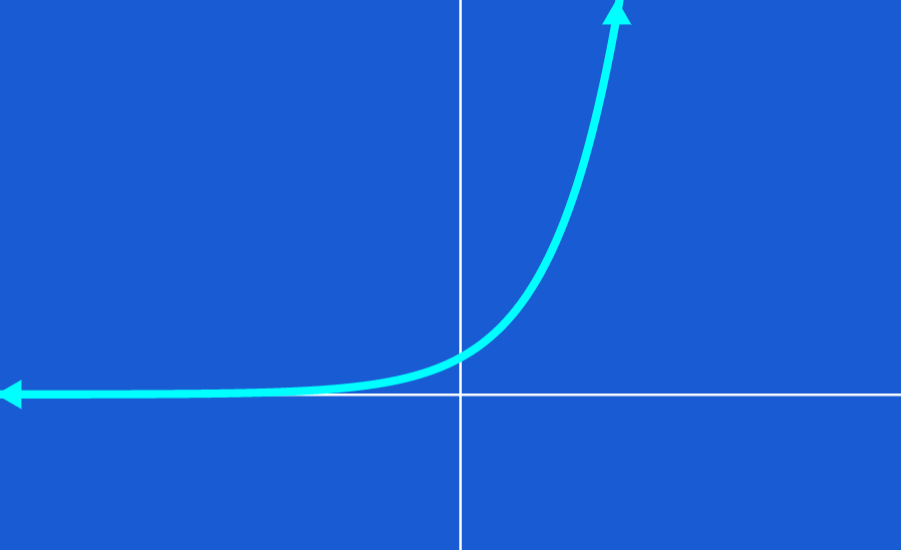
Las funciones exponenciales tienen la forma $latex y={{b}^{x}}$, en donde $latex b>0$. Las funciones exponenciales son funciones que permanecen proporcionales a su valor original a medida que crece o decrece. Si es que b>1, la función crece y si es que 1>b>0, la función decrece.
En este artículo, aprenderemos sobre las gráficas de funciones exponenciales y conoceremos sus propiedades. Veremos algunos ejemplos de práctica.
Definiciones
En su forma más básica, una función exponencial puede ser considerada como una función en donde la variable aparece en el exponente. La función exponencial más simple es una función de la forma $latex y={{b}^{x}}$, en donde b es un número positivo.
Cuando tenemos $latex b>1$, la función crece en una manera que es proporcional a su valor original. Esto es llamado crecimiento exponencial.
Cuando tenemos $latex 1>b>0$, la función decrece en una manera que es proporcional a su valor original. Esto es llamado decrecimiento exponencial.
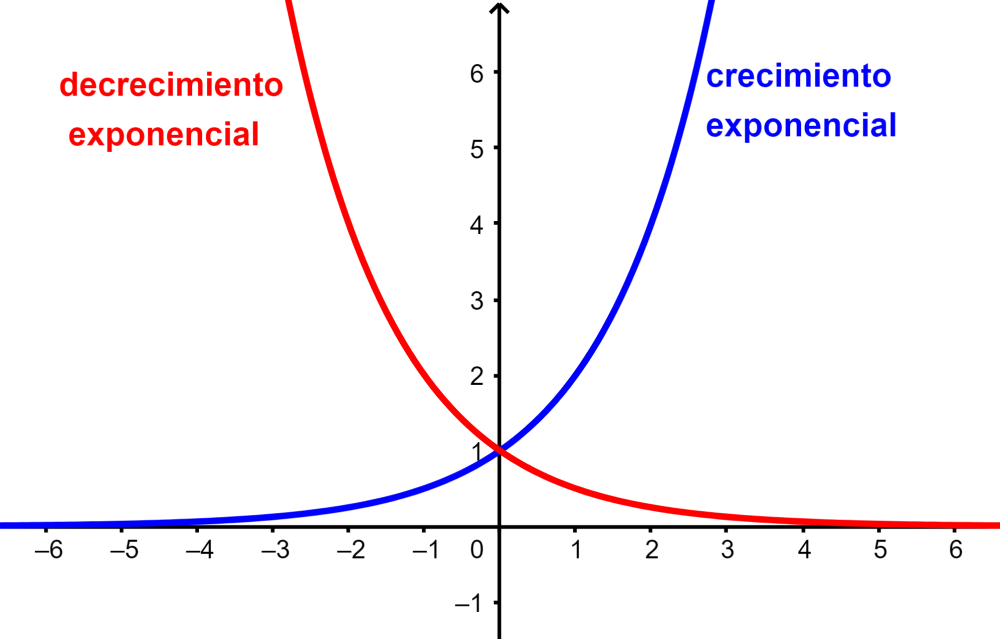
Gráficas de funciones exponenciales
Miremos los siguientes ejemplos de cómo graficar funciones exponenciales.
EJEMPLO 1
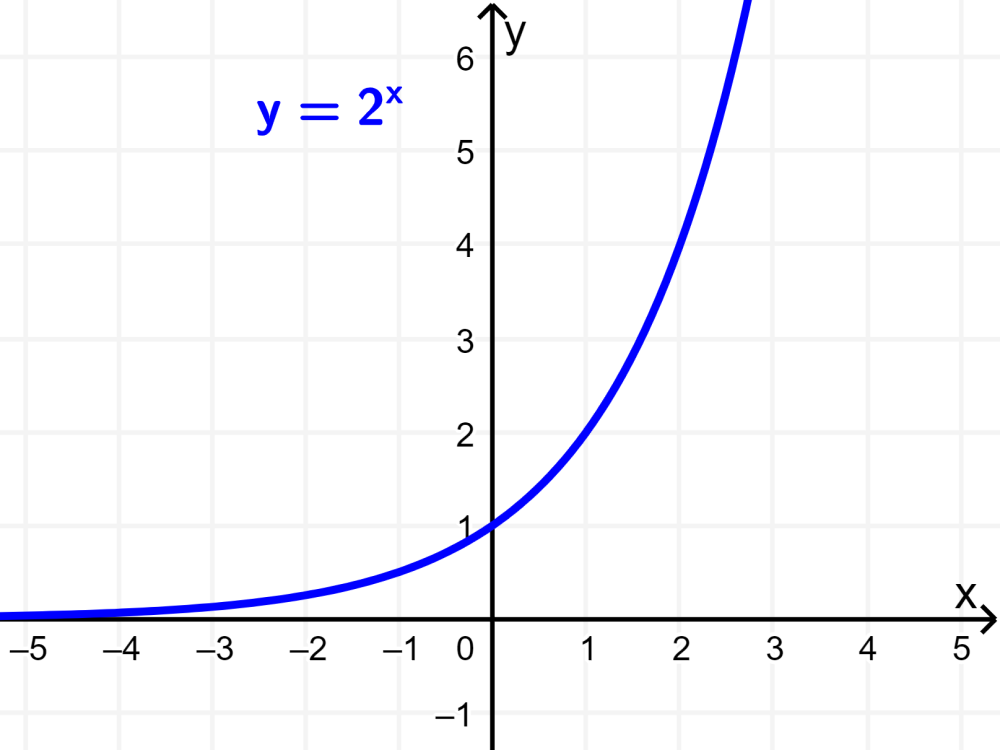
Supongamos que queremos graficar la función $latex y={{2}^{x}}$. Una forma para lograr esto es escoger valores para x y usarlos en la función para generar valores para y. Al hacerlo, podemos obtener los siguientes puntos:
$$\left( {-2,\frac{1}{4}} \right),~\left( {-1,\frac{1}{2}} \right),~\left( {0,~1} \right),~\left( {1,~2} \right)$$ y $latex ( {2,~4}).$
A medida que conectamos estos puntos, podemos observar que formamos una curva que cruza al eje y a través del punto (0, 1). Esta gráfica incrementa a medida que los valores de x se hacen más grandes. Podemos ver que esta gráfica tiende a infinito a medida que los valores de x tienen a infinito.
De igual forma, podemos ver que a medida que los valores de x se hacen más y más pequeños, la curva se acerca más y más al eje x. La curva se acerca a cero a medida que los valores de x se acercan a infinito negativo. Dado que la curva nunca toca al eje x, tenemos que el eje x es una asíntota horizontal de la función.
Para cualquier función exponencial de la forma $latex y={{b}^{x}}$, en donde tenemos que $latex b>1$, tenemos al punto (1, b) en la gráfica.
EJEMPLO 2
Ahora, consideremos a la función $latex y={{\left( {\frac{1}{2}} \right)}^{x}}$ cuando $latex 1>b>0$. Similar al ejemplo anterior, podemos graficar esta función exponencial al usar varios valores de x y sustituirlos en la función para obtener valores de y y formar las siguientes coordenadas cartesianas:
$$ \left( {-2, 4} \right),~\left( {-1, 2} \right),~\left( {0,~1} \right),~\left( {1,~\frac{1}{2}} \right)$$ y $latex ( {2, \frac{1}{4}}).$
Cuando conectamos los puntos formados por esas coordenadas cartesianas, vemos que la curva que es formada cruza al eje y a través del punto (0, 1). La gráfica de esta función exponencial decrece a medida que los valores de x se hacen más grandes.
La gráfica se acerca a cero a medida que los valores de x tienden a infinito. Esto significa que la gráfica tiene una asíntota horizontal en el eje x. También podemos observar que la gráfica tiende a infinito a medida que los valores de x tienen a infinito negativo.
Para cualquier función exponencial de la forma $latex y={{b}^{x}}$, en donde tenemos que $latex 1>b>0$, tenemos al punto (1, b) en la gráfica.
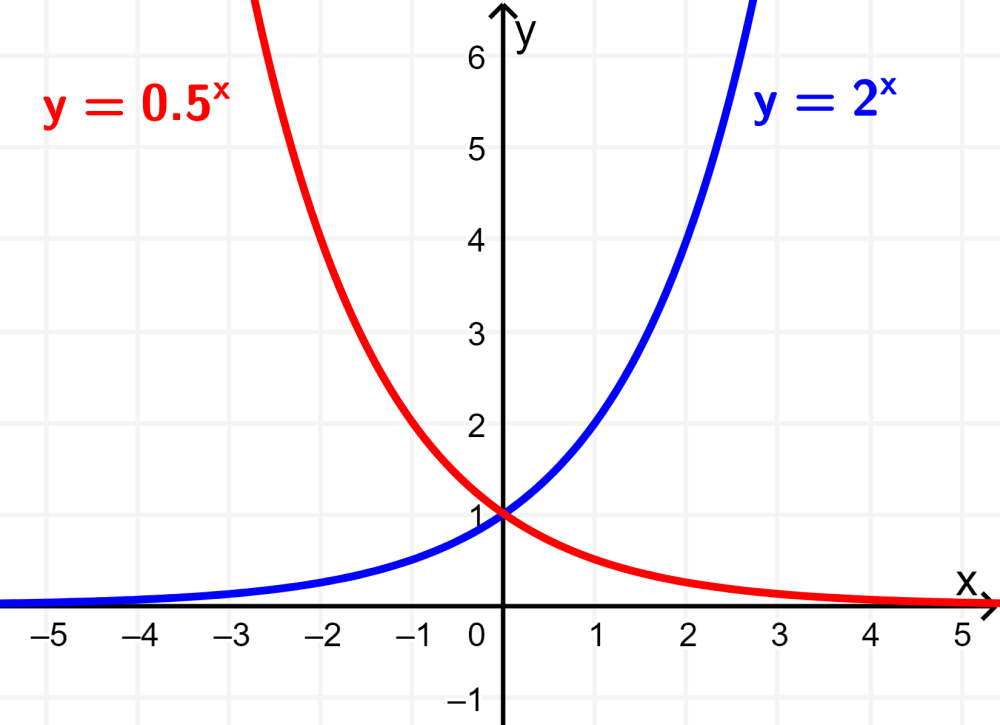
Al comparar sus gráficas, podemos ver que la gráfica de $latex y={{\left( {\frac{1}{2}} \right)}^{x}}$ es simétrica a la gráfica de $latex y={{2}^{x}}$ con respecto al eje y:
Limitaciones de b a números positivos
El valor de b está limitado a números mayores que 1 debido a las siguientes razones:
- Si es que tenemos $latex b=1$, la función se vuelve $latex y={{1}^{x}}$. Sabemos que 1 elevado a cualquier potencia es igual 1, por lo que en realidad tedríamos la función $latex y=1$. Esta función produce una línea horizontal, por lo que no obtendríamos una función exponencial.
- Si es que b es negativo, entonces, cuando elevamos a b a una potencia par, obtendremos números positivos. Sin embargo, cuando elevamos a b a una potencia impar, obtendremos números negativos. Esto significa que es imposible unir los puntos en una manera significativa, por lo que no obtendremos una forma parecida a las gráficas mostradas arriba.
Propiedades de gráficas exponenciales
Las siguientes son propiedades que todas las gráficas exponenciales comparten:
- El punto (0, 1) siempre está en la gráfica de la función exponencial de la forma $latex y={{b}^{x}}$, debido a que b es un número positivo y todos los números positivos elevados a la potencia de cero son iguales a 1.
- El punto (1, b) siempre está en la gráfica de la función exponencial de la forma $latex y={{b}^{x}}$. Esto es debido a que cualquier número b elevado a la potencia de 1 es igual a b.
- La función $latex y={{b}^{x}}$ siempre producirá valores positivos. Dado que b es un número positivo, siempre obtendremos valores positivos cuando sea elevado a cualquier potencia.
- El eje x es una asíntota horizontal de la función $latex y={{b}^{x}}$ debido a que la función siempre se acercará al eje x a medida que x tiende a infinito positivo o negativo, pero nunca cruza al eje x ya que la función nunca es igual a 0.
Véase también
¿Interesado en aprender más sobre gráficas de funciones? Mira estas páginas: