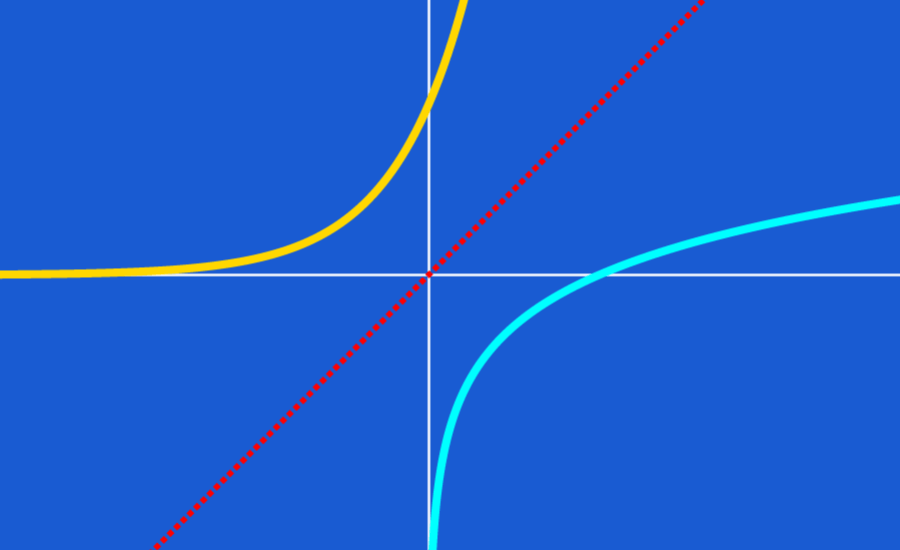
La función logarítmica $latex y={{\log }_{b}}x$ está definida como la función inversa de la función exponencial $latex y={{b}^{x}}$. Sabiendo esto, podemos graficar las funciones logarítmicas al mirar a la relación entre las funciones logarítmicas y funciones exponenciales.
Miraremos varias gráficas de funciones logarítmicas resueltas con traslaciones horizontales y verticales.
- Términos importantes
- ¿Cómo obtener gráficas de funciones logarítmicas?
- Gráficas de funciones logarítmicas básicas
- Gráficas de funciones logarítmicas con traslación horizontal
- Gráficas de funciones logarítmicas con traslación vertical
- Gráficas de funciones logarítmicas con traslación horizontal y vertical
- Véase también
Términos importantes
Antes de empezar con las gráficas de las funciones logarítmicas, es importante que nos familiaricemos con algunos términos que serán usados.
Dominio de una función
El dominio de una función es el conjunto de valores que podemos sustituir en la función para obtener respuestas aceptables. Es decir, el dominio son todos los valores posibles para x.
Rango de una función
El rango es el conjunto de valores que obtenemos al sustituir los valores en el dominio de la variable.
Asíntotas
Una asíntota es una línea a la que se acerca una curva a medida que los valores de x o y tienden a infinito. Tenemos tres tipos de asíntotas: verticales, horizontales e inclinadas. La asíntota vertical es el valor de x en el que la función crece sin límites cuando está cerca a ese valor.
La asíntota horizontal es un valor de y al que la función se acerca a medida que los valores de x crecen sin límites. Las asíntotas inclinadas son ecuaciones lineales a las que la función se acerca cuando los valores de x tienden a infinito.
¿Cómo obtener gráficas de funciones logarítmicas?
Podemos graficar una función logarítmica al examinar la gráfica de una función exponencial y luego intercambiar los valores de x y y.
La gráfica de una función exponencial $latex y={{b}^{x}}$ tiene las siguientes características:
- El dominio de una función exponencial es todos los números reales. Es decir, los valores de x van desde infinito negativo hasta infinito positivo.
- El rango es todos los números positivos reales. Es decir, desde 0 hasta infinito positivo.
- La gráfica de una función exponencial normalmente pasa a través del punto (0, 1), lo que significa que este punto es el intercepto en y.
- La gráfica de una función exponencial $latex y={{b}^{x}}$ tiene una asíntota horizontal en $latex y=0$.
- Si es que tenemos $latex 1>b>0$, la función decrece de izquierda a derecha y es denominada decrecimiento exponencial.
- Si es que tenemos $latex b>1$, la gráfica incrementa de izquierda a derecha y es llamada crecimiento exponencial.
Usando cada una de las características mencionadas, podemos deducir características equivalentes para las funciones logarítmicas:
- El dominio de una función logarítmica es todos los números positivos reales, desde el 0 hasta positivo infinito.
- El rango de una función exponencial es todos los números reales.
- La gráfica de una función logarítmica pasa a través del punto (1, 0).
- La gráfica de una función logarítmica tiene una asíntota vertical en $latex x=0$.
- Si es que tenemos $latex 1>b>0$, la gráfica decrecerá de izquierda a derecha.
- Si es que tenemos $latex b>1$, la gráfica crecerá de izquierda a derecha.
Gráficas de funciones logarítmicas básicas
Podemos considerar a una función logarítmica básica como una función que no tiene traslaciones horizontales o verticales.
Podemos graficar funciones logarítmicas básicas siguiendo los siguientes pasos:
Paso 1: Todas las funciones logarítmicas básicas pasan por el punto (1, 0), por lo que empezamos graficando ese punto.
Paso 2: Sabemos que la gráfica tiene una asíntota en x=0, por lo que la trazamos.
Paso 3: Si es que la base de la función es mayor que 1, la gráfica incrementa de izquierda a derecha. Si es que la base de la función está entre 0 y 1, la gráfica decrece de izquierda a derecha.
EJEMPLO 1
Grafica la función logarítmica $latex y={{\log }_{2}}x$.
Solución: Empezamos colocando un punto en (1, 0). Sabemos que la función logarítmica debe tener el dominio de (0, infinito) y el rango de (-infinito, infinito).
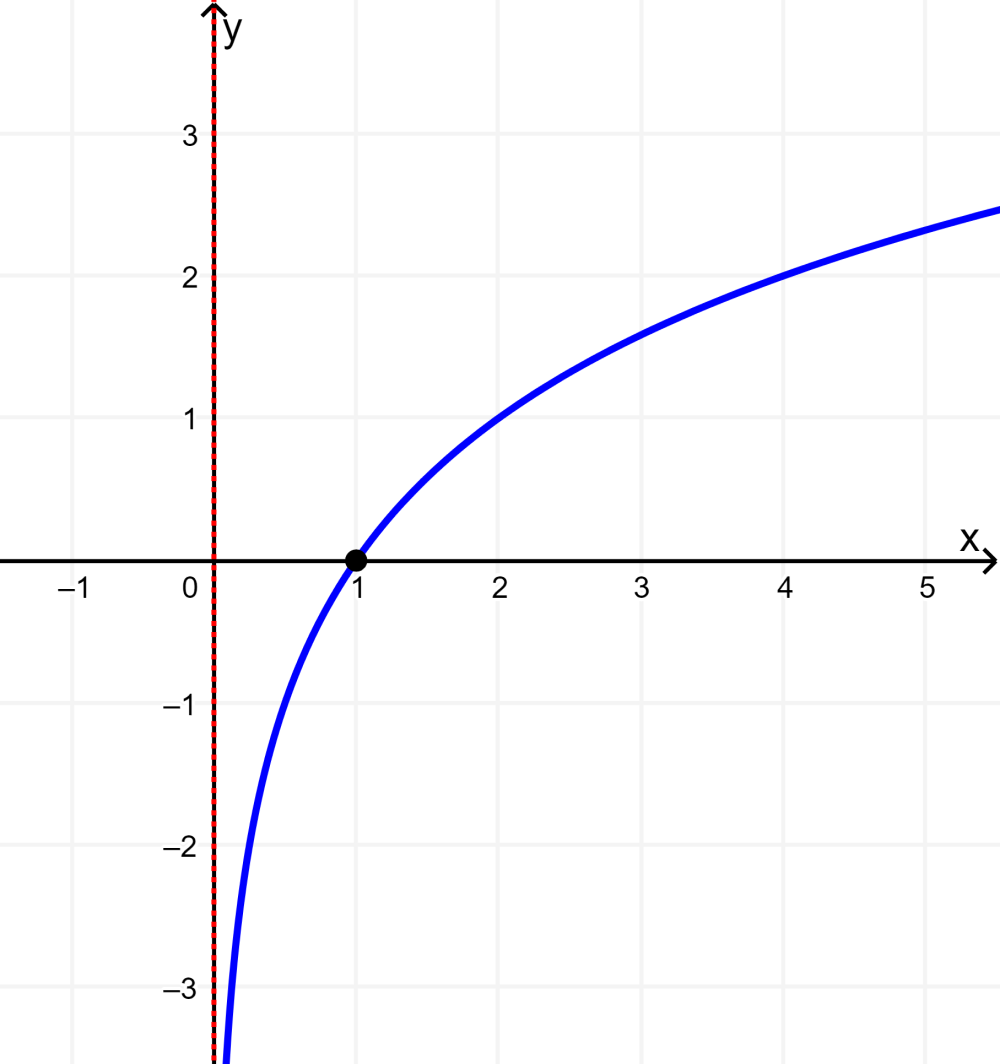
Dado que la función logarítmica $latex y={{\log }_{2}}x$ tiene una base que es mayor que 1, incrementamos la curva de izquierda a derecha como se muestra a continuación.
La asíntota horizontal no puede ser visualizada, ya que se ubica exactamente en el eje x.
EJEMPLO 2
Grafica la función logarítmica $latex y={{\log }_{0.5}}x$.
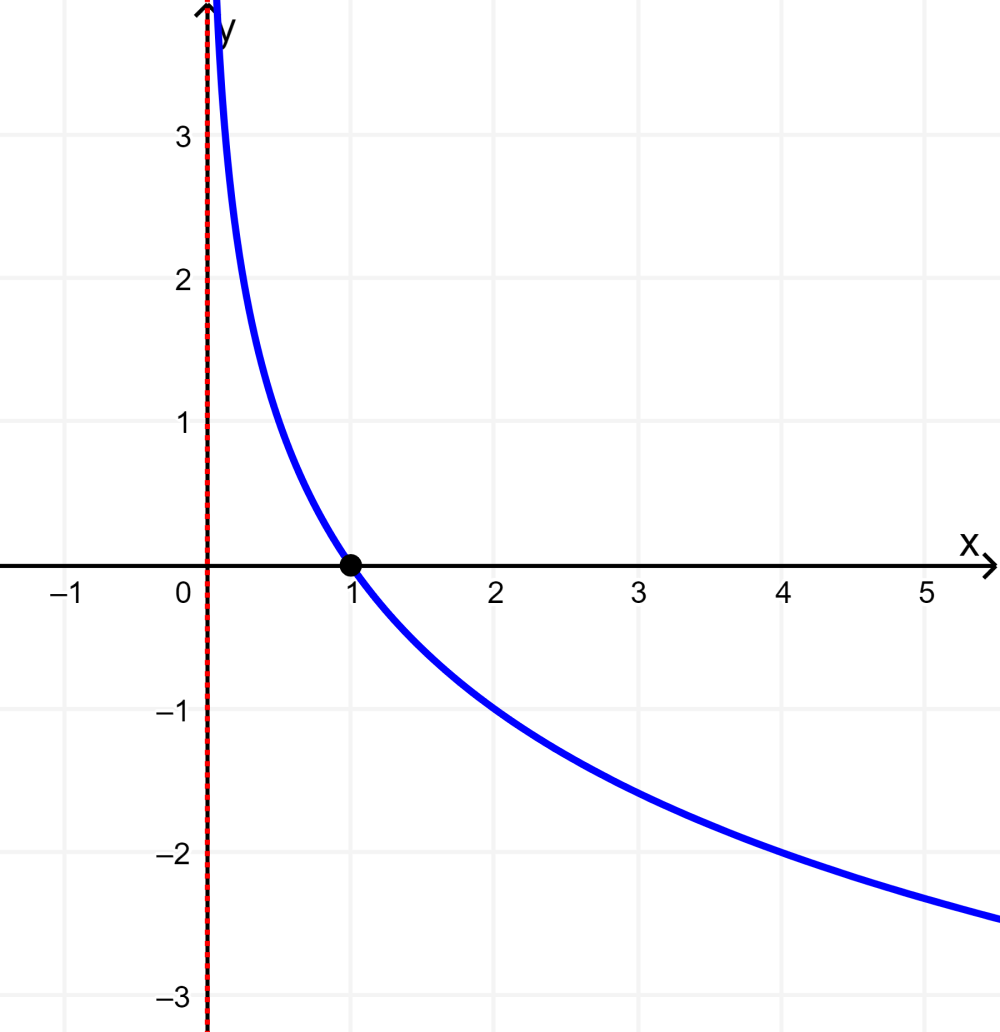
Solución: De igual forma, colocamos un punto en (1, 0). La función tiene el mismo dominio y rango que la anterior. El dominio es (0, infinito) y el rango es (-infinito, infinito).
La asíntota vertical se ubica exactamente en el eje y.
En este caso, la base de la función $latex y={{\log }_{0.5}}x$ es menor que 1, pero mayor que 0, por lo que la función decrece de izquierda a derecha.
Gráficas de funciones logarítmicas con traslación horizontal
Las funciones logarítmicas con traslación horizontal tienen la forma $latex y={{\log }_{b}}(x-h)$, en donde h es la traslación horizontal. Al aplicar una traslación horizontal, producimos los siguientes cambios en las gráficas:
- El intercepto en x se mueve hacia la derecha o hacia la izquierda una distancia que corresponde al valor de h.
- La asíntota vertical se mueve la misma distancia.
- El dominio de la función también es afectado.
EJEMPLO 1
Grafica la función logarítmica $latex y={{\log }_{2}}(x-3)$.
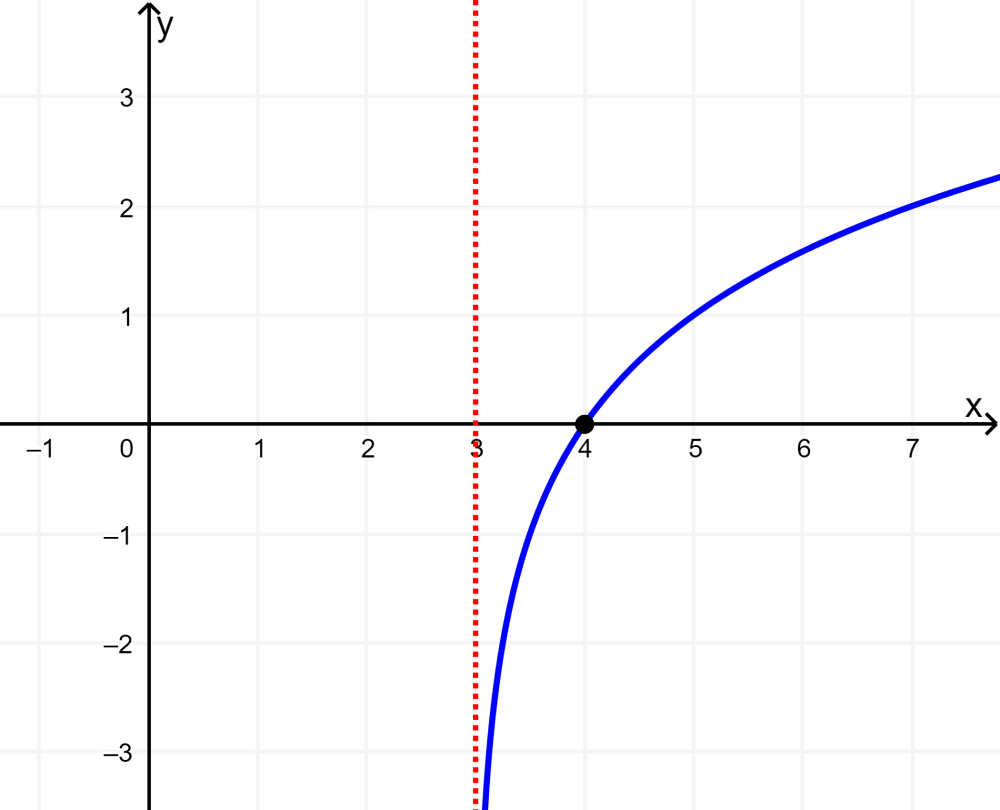
Solución: El intercepto en x se ubica en (4, 0). La función tiene el dominio (3, infinito) y el rango es (-infinito, infinito).
La asíntota vertical se ubica en x=3.
La base de la función es mayor que 1, por lo que la función crece de izquierda a derecha.
EJEMPLO 2
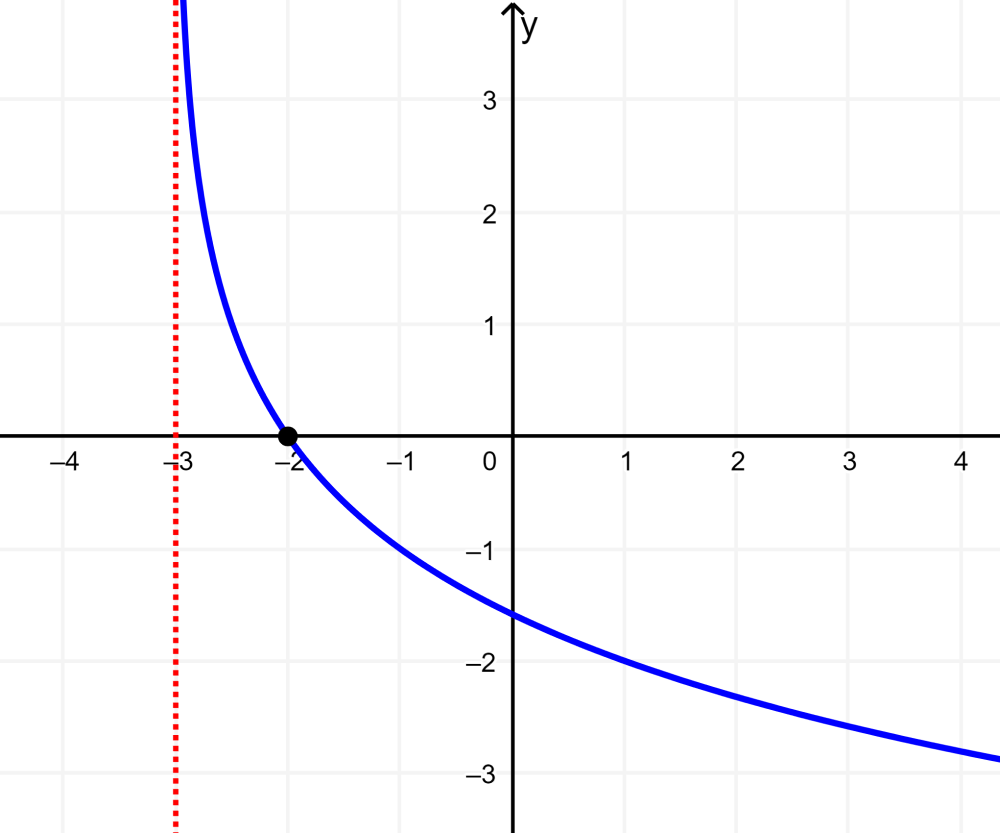
Grafica la función logarítmica $latex y={{\log }_{0.5}}(x+3)$.
Solución: El intercepto en x se ubica en (-2, 0). La función tiene el dominio (-3, infinito) y el rango es (-infinito, infinito).
La asíntota vertical se ubica en x=-3.
En este caso, la base de la función $latex y={{\log }_{0.5}}x$ es menor que 1, pero mayor que 0, por lo que la función decrece de izquierda a derecha.
Gráficas de funciones logarítmicas con traslación vertical
Una función logarítmica con traslación vertical tienen la forma $latex y={{\log }_{b}}(x)+k$, en donde k es la traslación vertical. Con una traslación vertical en la gráfica producimos lo siguiente:
- El intercepto en x se mueve hacia arriba o abajo por una distancia de k.
EJEMPLO
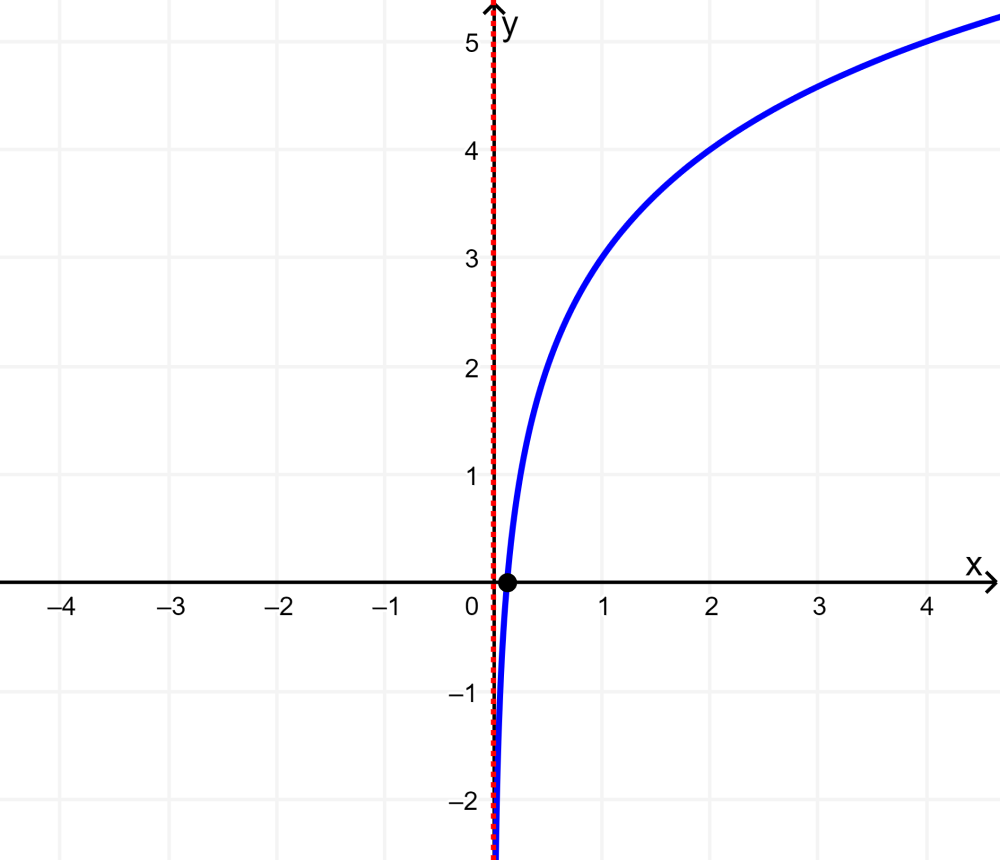
Grafica la función logarítmica $latex y={{\log }_{2}}(x)+3$.
Solución: La función logarítmica tiene el dominio (0, infinito) y el rango es (-infinito, infinito).
La asíntota vertical se ubica en x=0.
La función crece de izquierda a derecha, ya que su base es mayor que 1.
Gráficas de funciones logarítmicas con traslación horizontal y vertical
Una función logarítmica con traslación horizontal y vertical tiene la forma $latex y={{\log }_{b}}(x-h)+k$, en donde h es la traslación horizontal y k es la traslación vertical.
EJEMPLO 1
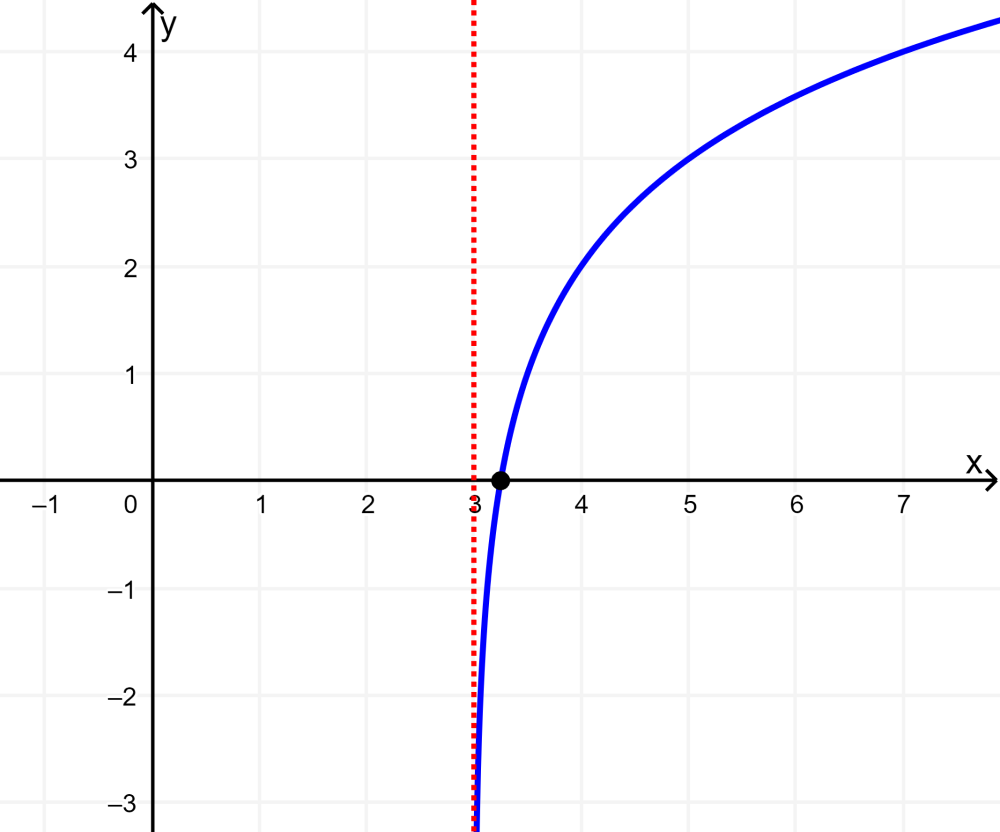
Grafica la función logarítmica $latex y={{\log }_{2}}(x-3)+2$.
Solución: La gráfica se traslada 3 unidades hacia la derecha y 2 unidades hacia arriba. La función tiene el dominio (3, infinito) y el rango es (-infinito, infinito).
La asíntota vertical se ubica en x=3.
La base de la función es mayor que 1, por lo que la función crece de izquierda a derecha..
EJEMPLO 2
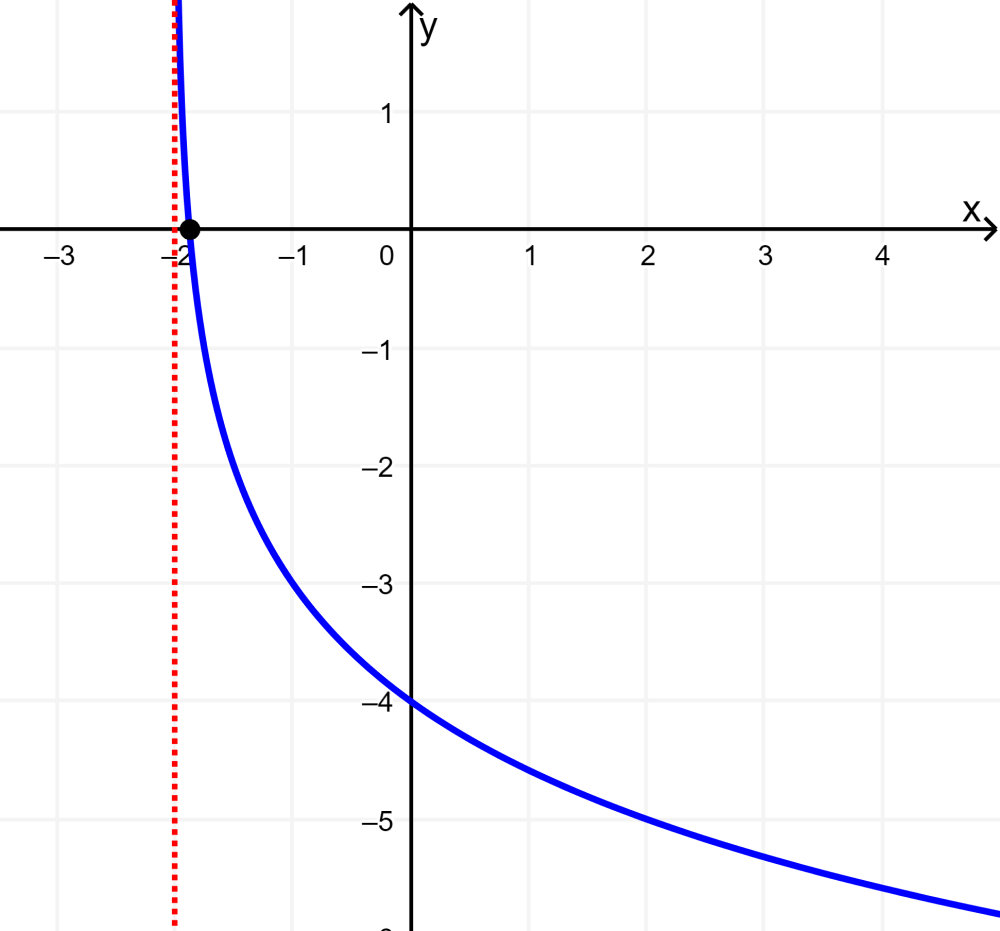
Grafica la función logarítmica $latex y={{\log }_{0.5}}(x+2)-3$.
Solución: La función original es trasladada 2 unidades hacia la izquierda y 3 unidades hacia abajo.
La asíntota vertical se ubica en x=-2.
En la función $latex y={{\log }_{0.5}}x$, la base es menor que 1 y mayor que 0, por lo que la función decrece de izquierda a derecha.
Véase también
¿Interesado en aprender más sobre gráficas de funciones? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
