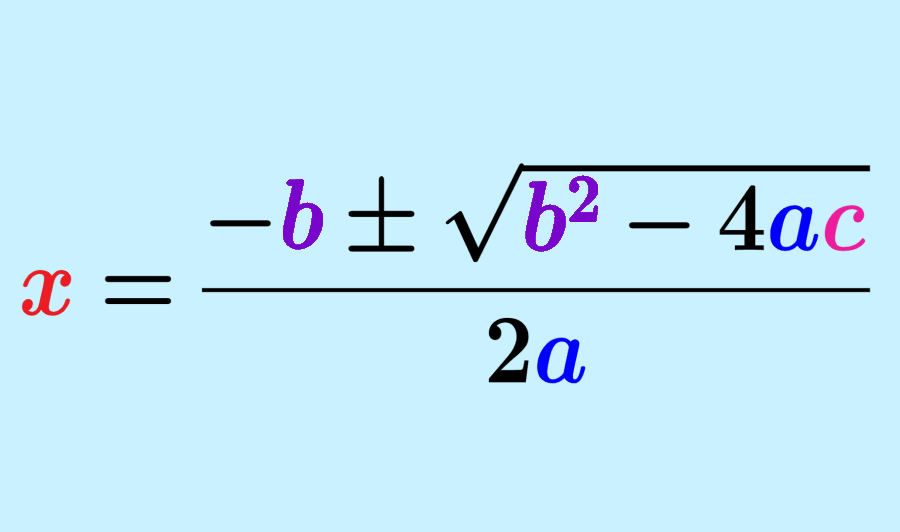Las ecuaciones cuadráticas son ecuaciones algebraicas que tienen la forma ax²+bx+c=0. Existen varios métodos que podemos usar para resolver ecuaciones cuadráticas dependiendo del tipo de ecuación cuadrática que tengamos. Sin embargo, resolver ecuaciones cuadráticas por la fórmula general es un método que siempre nos permite encontrar ambas soluciones a la ecuación.
A continuación, haremos una breve revisión de la fórmula cuadrática general. Luego, conoceremos cómo resolver ecuaciones cuadráticas con esta fórmula y miraremos algunos ejemplos de práctica.
ÁLGEBRA
Relevante para…
Aprender a resolver ecuaciones cuadráticas usando la fórmula general.
ÁLGEBRA
Relevante para…
Aprender a resolver ecuaciones cuadráticas usando la fórmula general.
¿Cómo resolver ecuaciones cuadráticas usando la fórmula general?
Para resolver ecuaciones cuadráticas usando la fórmula cuadrática general, tenemos que empezar escribiendo a la ecuación en la forma $latex a{{x}^2}+bx+c=0$. Una vez tengamos a la ecuación escrita en esa forma, simplemente reemplazamos los coeficientes a, b y c en la fórmula cuadrática:
| $$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$$ |
Nota: El signo ± es muy importante, ya que de esa forma obtendremos ambas soluciones a la ecuación cuadrática cuando sea el caso.
La cantidad que va dentro del signo de raíz cuadrada, es decir, $latex b^2-4ac$ es llamada el discriminante de la ecuación cuadrática.
El número de raíces y el tipo de raíces resultantes de la ecuación cuadrática dependen del valor del discriminante. Entonces, tenemos lo siguiente:
- Si es que $latex b^2-4ac>0$, la ecuación tiene dos raíces reales.
- Si es que $latex b^2-4ac<0$, la ecuación no tiene raíces reales.
- Si es que $latex b^2-4ac=0$, la ecuación tiene una raíz repetida.
En otras palabras, si es que el valor dentro de la raíz cuadrada es positivo, tendremos dos raíces reales. Si es que ese valor es negativo, no tendremos raíces reales (pero sí raíces imaginarias o complejas). Si es que ese valor es igual a cero, tenemos una sola raíz.
Si es que quieres conocer cómo derivar la fórmula cuadrática general, puedes visitar nuestro artículo Fórmula Cuadrática General – Derivación.
Ecuaciones cuadráticas por la fórmula general – Ejercicios resueltos
Los siguientes ejercicios son resueltos usando la fórmula cuadrática general. Cada ejercicio tiene su respectiva respuesta, pero intenta resolver los ejercicios tú mismo antes de mirar la solución.
EJERCICIO 1
Encuentra las soluciones a la ecuación $latex {{x}^2}+3x-4=0$ usando la fórmula cuadrática.
Solución
Usando los valores $latex a=1$, $latex b=3$ y $latex c=-4$ en la fórmula, tenemos:
$$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$$
$$x=\frac{-(3)\pm \sqrt{( 3)^2-4(1)(-4)}}{2(1)}$$
$$=\frac{-3\pm \sqrt{9+16}}{2}$$
$$=\frac{-3\pm \sqrt{25}}{2}$$
$$=\frac{-3\pm 5}{2}$$
$$=\frac{-3-5}{2},~~\frac{-3+5}{2}$$
$$=\frac{-8}{2},~\frac{2}{2}=-4,~1$$
Entonces, las soluciones son $latex x=-4$ y $latex x=1$.
EJERCICIO 2
Resuelve la ecuación $latex x^2-8x+4=0$, dando las respuestas con dos lugares decimales.
Solución
Tenemos los valores $latex a=1$, $latex b=-8$ y $latex c=4$. Entonces, tenemos:
$$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$$
$$x=\frac{-(-8)\pm \sqrt{( -8)^2-4(1)(4)}}{2(1)}$$
$$=\frac{8\pm \sqrt{64-16}}{2}$$
$$=\frac{8\pm \sqrt{48}}{2}$$
$$x=7.46 \text{ o } 0.54$$
Entonces, las soluciones son $latex x=7.46$ y $latex x=0.54$.
EJERCICIO 3
Usando la fórmula cuadrática general, muestra que la ecuación $latex 5x^2+4x+10=0$ no tiene soluciones reales.
Solución
Usando la fórmula cuadrática con los valore $latex a=5$, $latex b=4$ y $latex c=10$, tenemos:
$$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$$
$$x=\frac{-(4)\pm \sqrt{( 4)^2-4(5)(10)}}{2(5)}$$
$$=\frac{-5\pm \sqrt{16-200}}{10}$$
$$=\frac{-5\pm \sqrt{-184}}{10}$$
Tenemos un número negativo dentro de la raíz cuadrada. $latex \sqrt{-184}$ no es un número real, por lo que la ecuación no tiene raíces reales.
EJERCICIO 4
Resuelve la ecuación $latex x^2-10x+25=0$ usando la fórmula cuadrática.
Solución
Usamos los valores $latex a=1$, $latex b=-10$ y $latex c=25$ en la fórmula cuadrática y tenemos:
$$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$$
$$x=\frac{-(-10)\pm \sqrt{( -10)^2-4(1)(25)}}{2(1)}$$
$$=\frac{10\pm \sqrt{100-100}}{2}$$
$$=\frac{10\pm \sqrt{0}}{2}$$
$$=\frac{10}{2}$$
$$=5$$
En este caso, tenemos una sola raíz repetida $latex x=5$.
EJERCICIO 5
Encuentra las soluciones a la ecuación $latex x^2+2x-1=0$ expresándolas con dos lugares decimales.
Solución
Usnado la fórmula general con $latex a=1$, $latex b=2$ y $latex c=-1$, tenemos:
$$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$$
$$x=\frac{-(2)\pm \sqrt{( 2)^2-4(1)(-1)}}{2(1)}$$
$$=\frac{-2\pm \sqrt{4+4}}{2}$$
$$=\frac{-2\pm \sqrt{8}}{2}$$
$$x=-2.41 \text{ o }0.41$$
Entonces, las soluciones son $latex x=-2.41$ y $latex x=0.41$.
EJERCICIO 6
Resuelve la ecuación $latex 2x^2+3x-4=0$ usando la fórmula general. Expresa las soluciones con dos lugares decimales.
Solución
Tenemos los valores $latex a=2$, $latex b=3$ y $latex c=-4$. Entonces, tenemos:
$$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$$
$$x=\frac{-(3)\pm \sqrt{( 3)^2-4(2)(-4)}}{2(2)}$$
$$=\frac{-3\pm \sqrt{9+32}}{4}$$
$$=\frac{-3\pm \sqrt{41}}{2}$$
$$=-2.35 \text{ o }0.85$$
Las soluciones de la ecuación son $latex x=-2.35$ y $latex x=0.85$.
EJERCICIO 7
¿Cuáles son las soluciones a la ecuación $latex 3x^2+x-3=0$ en dos lugares decimales?
Solución
Usando los valores $latex a=3$, $latex b=1$ y $latex c=-3$ en la fórmula general, tenemos:
$$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$$
$$x=\frac{-(1)\pm \sqrt{( 1)^2-4(3)(-3)}}{2(3)}$$
$$=\frac{-1\pm \sqrt{1+36}}{6}$$
$$=\frac{-1\pm \sqrt{37}}{6}$$
$$x=-1.18\text{ o }0.85$$
Las soluciones de la ecuación son $latex x=-1.18$ y $latex x=0.85$.
Ecuaciones cuadráticas por la fórmula general – Ejercicios para resolver
Resuelve los siguientes ejercicios usando la fórmula cuadrática general. Haz clic en «Verificar» para comprobar que tu respuesta es la correcta.
Véase también
¿Interesado en aprender más sobre ecuaciones cuadráticas? Puedes mirar estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
