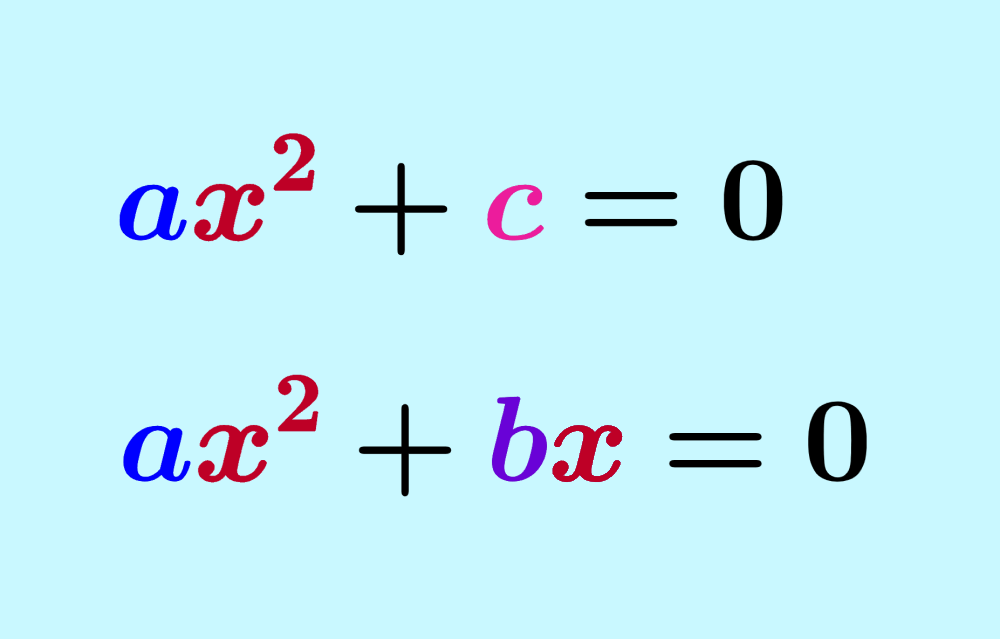Una ecuación cuadrática incompleta es una ecuación cuadrática que no tienen un término de la forma ax²+bx+c=0 (siempre y cuando el término x² siempre esté presente). Estas ecuaciones generalmente son más fáciles de resolver que una ecuación cuadrática completa. Dependiendo del término faltante, tenemos dos tipos de ecuaciones cuadráticas incompletas.
A continuación, conoceremos los dos tipos de ecuaciones cuadráticas incompletas detalladamente. Aprenderemos a resolver este tipo de ecuaciones y miraremos algunos ejemplos de práctica.
¿Cómo resolver ecuaciones cuadráticas incompletas?
Para resolver ecuaciones cuadráticas incompletas, tenemos que empezar determinando cuál es el término faltante de la ecuación cuadrática dada en la forma $latex ax^2+bx+c=0$. Dependiendo de esto, podemos usar dos métodos diferentes para encontrar las soluciones de la ecuación.
Resolver ecuaciones cuadráticas que no tienen el término bx
Estas ecuaciones cuadráticas tienen la forma $latex ax^2+c=0$ y no tienen el término bx. Para resolver estas ecuaciones, tenemos que despejar a x² y luego sacar la raíz cuadrada de ambos lados de la ecuación.
Por ejemplo, vamos a resolver la ecuación $latex x^2-16=0$. Entonces, tenemos que reorganizarla de la siguiente manera:
$latex x^2=16$
Ahora, sacamos la raíz cuadrada de ambos lados:
$latex x=\sqrt{16}$
$latex x=\pm 4$
Nota: La solución negativa también debe ser considerada porque $latex (-4)^2=16$.
Resolver ecuaciones cuadráticas que no tienen el término c
Estas ecuaciones cuadráticas tienen la forma $latex ax^2+bx=0$ y no tienen el término constante c. Para resolver estas ecuaciones, tenemos que factorizar la x del lado izquierdo de la ecuación, formar una ecuación con cada factor y luego resolver.
Por ejemplo, vamos a resolver la ecuación $latex x^2-7x=0$. Entonces, la factorizamos de la siguiente manera:
$latex x(x-7)=0$
Ahora, formamos una ecuación con cada factor y resolvemos:
$latex x=0~~$ o $latex ~~x-7=0$
$latex x=0~~$ o $latex ~~x=7$
Nota: En este tipo de ecuaciones, una de las soluciones siempre sera $latex x=0$.
Ecuaciones cuadráticas incompletas – Ejercicios resueltos
Los métodos para resolver ambos tipos de ecuaciones cuadráticas incompletas son usados en los siguientes ejercicios. Intenta resolver los ejercicios tú mismo antes de mirar la solución.
EJERCICIO 1
Encuentra las soluciones de la ecuación $latex x^2-4=0$.
Solución
Esta ecuación cuadrática no tiene el término bx. Entonces, podemos resolverla al despejar al término cuadrático y sacar la raíz cuadrada de ambos lados de la ecuación:
$latex x^2-4=0$
$latex x^2=4$
$latex x=\pm\sqrt{4}$
$latex x=\pm 2$
Las soluciones de la ecuación son $latex x=2$ y $latex x=-2$.
EJERCICIO 2
Encuentra las soluciones de la ecuación $latex x^2+4x=0$.
Solución
Esta ecuación no tiene el término constante c. Entonces, para resolverla, tenemos que factorizar la x y formar una ecuación con cada factor:
$latex x^2+4x=0$
$latex x(x+4)=0$
$latex x=0 ~~$ o $latex ~~x+4=0$
$latex x=0 ~~$ o $latex ~~x=-4$
Las soluciones de la ecuación son $latex x=0$ y $latex x=-4$
EJERCICIO 3
Encuentra las raíces de la ecuación $latex x^2-10=0$.
Solución
Para resolver esta ecuación, tenemos que despejar al término cuadrático y sacar la raíz cuadrada de ambos lados:
$latex x^2-10=0$
$latex x^2=10$
$latex x=\pm\sqrt{10}$
Las raíces de la ecuación son $latex \sqrt{10}$ y $latex -\sqrt{10}$.
EJERCICIO 4
¿Cuáles son las raíces de la ecuación $latex x^2-10x=0$?
Solución
Para resolver esta ecuación, tenemos que factorizar a la x de ambos términos y luego formamos una ecuación con cada factor de la ecuación cuadrática:
$latex x^2-10x=0$
$latex x(x-10)=0$
$latex x=0 ~~$ o $latex ~~x-10=0$
$latex x=0 ~~$ o $latex ~~x=10$
Las raíces de la ecuación son $latex x=0$ y $latex x=10$.
EJERCICIO 5
Demuestra que la ecuación $latex x^2+9=0$ no tiene raíces reales.
Solución
Podemos despejar al término cuadrático y luego sacar la raíz cuadrada de ambos lados de la ecuación:
$latex x^2+9=0$
$latex x^2=-9$
$latex x=\pm\sqrt{-9}$
Vemos que obtuvimos una raíz cuadrada de un número negativo. Entonces, la ecuación cuadrática no tiene raíces reales.
Nota: Si es que usamos números imaginarios, la ecuación tiene dos raíces complejas.
EJERCICIO 6
Determina las raíces de la ecuación $latex 4x^2+8x=0$.
Solución
En este caso, podemos factorizar el término 4x de la ecuación. Luego, formamos una ecuación con cada término y resolvemos:
$latex 4x^2+8x=0$
$latex 4x(x+2)=0$
$latex 4x=0 ~~ $ o $latex ~~x+2=0$
$latex x=0 ~~$ o $latex ~~x=-2$
Las soluciones de la ecuación son $latex x=0$ y $latex x=-2$.
EJERCICIO 7
Encuentra las soluciones de la ecuación $latex 4x^2-20=0$.
Solución
Para resolver esta ecuación, tenemos que despejar a x² y luego sacar la raíz cuadrada de ambos lados de la ecuación:
$latex 4x^2-20=0$
$latex 4x^2=20$
$latex x^2=5$
$latex x=\pm\sqrt{5}$
Las soluciones de la ecuación son $latex \sqrt{5}$ y $latex -\sqrt{5}$.
Ecuaciones cuadráticas incompletas – Ejercicios para resolver
Resuelve los siguientes ejercicios aplicando los métodos de resolución de ecuaciones cuadráticas incompletas.
Véase también
¿Interesado en aprender más sobre ecuaciones cuadráticas? Puedes mirar estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
