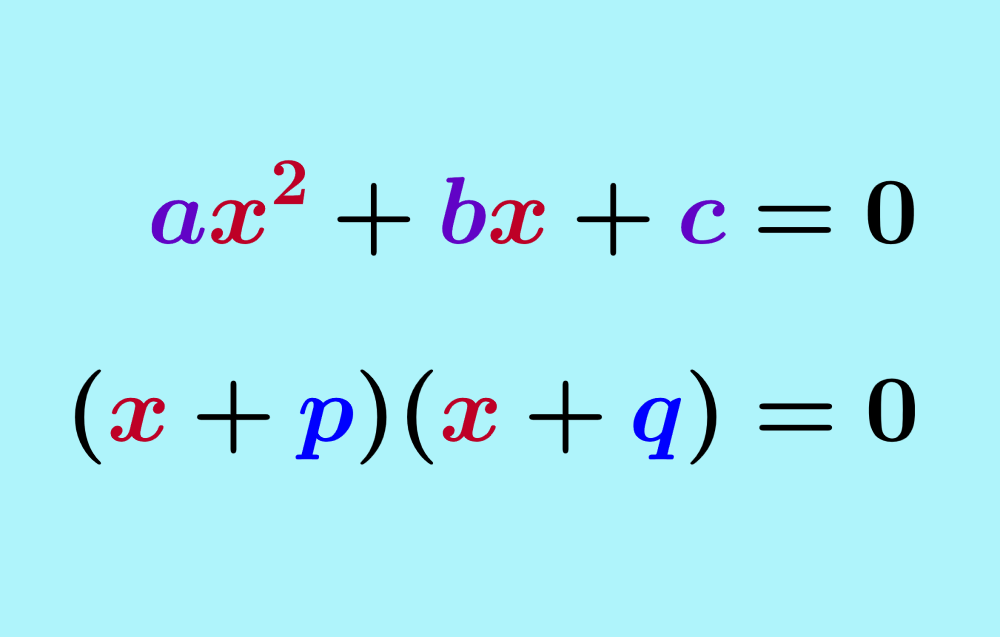Una ecuación cuadrática de la forma ax²+bx+c=0 puede ser resuelta usando el método de factorización. Para esto, tenemos que factorizar la ecuación usando cualquier método que sea aplicable para escribirla en la forma (x+p)(x+q)=0. Al formar una ecuación con cada factor, encontraremos que las raíces de la ecuación cuadrática son x=-p y x=-q.
A continuación, aprenderemos cómo resolver ecuaciones cuadráticas usando el método de factorización. Además, usaremos este método para resolver algunos ejercicios de práctica.
ÁLGEBRA
Relevante para…
Aprender a resolver ecuaciones cuadráticas por factorización.
ÁLGEBRA
Relevante para…
Aprender a resolver ecuaciones cuadráticas por factorización.
¿Cómo resolver ecuaciones cuadráticas por factorización?
Para resolver una ecuación cuadrática por el método de factorización, tenemos que seguir los siguientes pasos:
Paso 1: Simplificar y escribir a la ecuación en la forma $latex ax^2+bx+c=0$.
Paso 2: Factorizar la ecuación cuadrática usando cualquier método, de modo que podamos escribirla en la forma $latex (x+p)(x+q)=0$.
Paso 3: Formar una ecuación con cada factor al igualarlo a cero. Por ejemplo $latex x+p=0$.
Paso 4: Resolver la ecuación de cada factor.
Recordemos que factorizar una ecuación cuadrática consiste en escribir a una ecuación de la forma $latex x^2+bx+c=0$ a la forma $latex (x+p)(x+q)=0$. Para lograr esto, tenemos que encontrar dos factores, los cuales al ser multiplicados, resulten en la ecuación cuadrática original.
Por ejemplo, la ecuación $latex x^2+2x-3=0$ puede ser factorizada en la forma $latex (x+3)(x-2)=0$, ya que al multiplicar los factores, obtenemos la ecuación original.
Si es que necesitas aprender o reforzar las técnicas de factorización de ecuaciones cuadráticas, puedes visitar nuestro artículo: Factorización de Ecuaciones Cuadráticas.
Resolver ecuaciones cuadráticas por factorización – Ejercicios resueltos
Los siguientes ejercicios son resueltos aplicando el método de factorización. Intenta resolver los ejercicios tú mismo antes de mirar la solución.
EJERCICIO 1
Resuelve la ecuación $latex x^2+5x+6=0$.
Solución
Factorizando el lado izquierdo de la ecuación, tenemos:
$latex x^2+5x+6=0$
$latex (x+2)(x+3)=0$
$latex x+2=0~~$ o $latex ~~x+3=0$
$latex x=-2~~$ o $latex ~~x=-3$
Las soluciones de la ecuación son $latex x=-2$ y $latex x=-3$.
EJERCICIO 2
Encuentra las soluciones de la ecuación $latex x^2+2x-8=0$.
Solución
Vamos a factorizar el lado izquierdo de la ecuación y luego formamos ecuaciones con los factores para encontrar las soluciones:
$latex x^2+2x-8=0$
$latex (x+4)(x-2)=0$
$latex x+4=0~~$ o $latex ~~x-2=0$
$latex x=-4~~$ o $latex ~~x=2$
Las soluciones de la ecuación son $latex x=-4$ y $latex x=2$.
EJERCICIO 3
Resuelve la ecuación $latex 2x^2-13x-24=0$ usando el método de factorización.
Solución
Factorizando el lado izquierdo de la ecuación, tenemos:
$latex 2x^2-13x-24=0$
$latex (2x+3)(x-8)=0$
$latex 2x+3=0~~$ o $latex ~~x-8=0$
$latex x=-\frac{3}{2}~~$ o $latex ~~x=8$
Las soluciones de la ecuación son $latex x=-\frac{3}{2}$ y $latex x=8$.
EJERCICIO 4
Resuelve la ecuación $latex x^2-x-10=x+5$ usando el método de factorización.
Solución
Primero, tenemos que simplificar y escribir a la ecuación en la forma $latex ax^2+bx+c=0$. Luego, la factorizamos y encontramos sus raíces:
$latex x^2-x-10=x+5$
$latex x^2-2x-15=0$
$latex (x+3)(x-5)=0$
$latex x+3=0~~$ o $latex ~~x-5=0$
$latex x=-3~~$ o $latex ~~x=5$
Las soluciones son $latex x=-3$ y $latex x=-5$.
EJERCICIO 5
Usa el método de factorización para resolver la ecuación $latex 3x^2-10x+3=0$
Solución
Factorizamos el lado izquierdo de la ecuación, formamos una ecuación con cada factor y resolvemos:
$latex 3x^2-10x+3=0$
$latex (3x-1)(x-3)=0$
$latex 3x-1=0~~$ o $latex ~~x-3=0$
$latex x=\frac{1}{3}~~$ o $latex ~~x=3$
Las raíces de la ecuación son $latex x=\frac{1}{3}$ y $latex x=3$.
EJERCICIO 6
Encuentra las soluciones de la ecuación $latex 5x^2 -5x-10=0$.
Solución
Podemos empezar dividiendo por 5 a ambos lados de la ecuación para simplificarla. Luego, factorizamos el lado izquierdo y resolvemos para los factores:
$latex 5x^2-5x-10=0$
$latex x^2-x-2=0$
$latex (x+1)(x-2)=0$
$latex x+1=0~~$ o $latex ~~x-2=0$
$latex x=-1~~$ o $latex ~~x=2$
Las soluciones de la ecuación son $latex x=-1$ y $latex x=2$.
EJERCICIO 7
Resuelve la ecuación $latex 3x^2+14x-12=2x^2+15x$ usando el método de factorización.
Solución
Para factorizar esta ecuación, tenemos que empezar simplificándola y escribirla en la forma $latex ax^2+bx+c=0$. Luego, la factorizamos y resolvemos para los factores:
$latex 3x^2+14x-12=2x^2+15x$
$latex x^2-x-12=0$
$latex (x+3)(x-4)=0$
$latex x+3=0~~$ o $latex ~~x-4=0$
$latex x=-3~~$ o $latex ~~x=4$
Las soluciones de la ecuación son $latex x=-3$ y $latex x=4$.
Resolver ecuaciones cuadráticas por factorización – Ejercicios para resolver
Usa el método de factorización para encontrar las soluciones de las siguientes ecuaciones cuadráticas.
Véase también
¿Interesado en aprender más sobre ecuaciones cuadráticas? Puedes mirar estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
