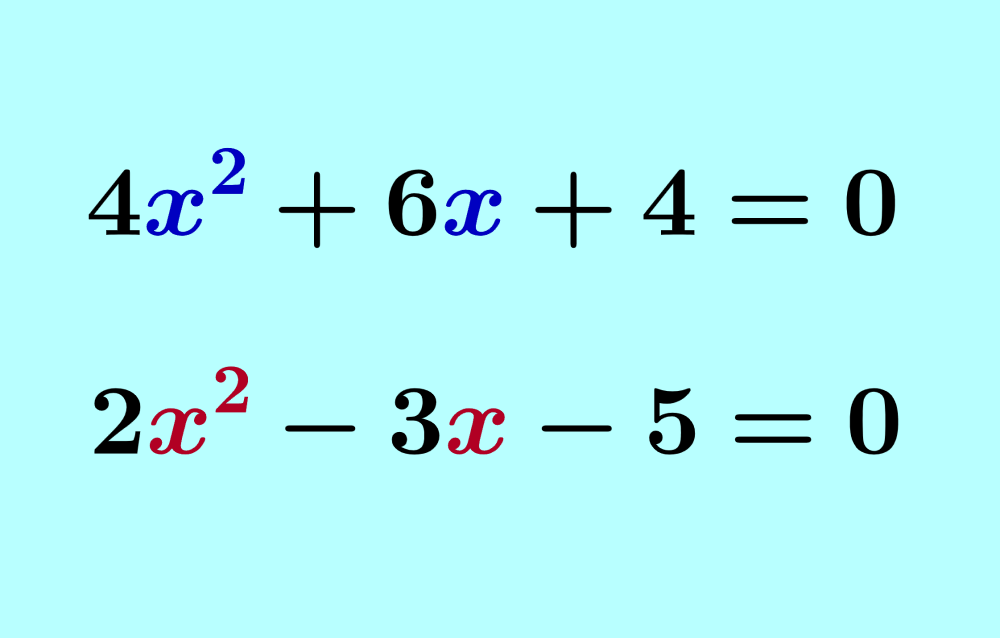Una ecuación cuadrática es una ecuación algebraica de segundo grado que tiene la forma ax²+bx+c=0. Podemos usar varios métodos para resolver ecuaciones cuadráticas. Dependiendo del tipo de ecuación que tengamos, unos métodos serán más fáciles que otros. Algunos de los métodos más importantes incluyen completar el cuadrado, usar factorización o usar la fórmula cuadrática.
A continuación, aprenderemos varios métodos para resolver ecuaciones cuadráticas paso a paso. Luego, aplicaremos estos métodos para resolver algunos ejercicios de práctica.
- Pasos para resolver ecuaciones cuadráticas incompletas
- Pasos para resolver ecuaciones cuadráticas por factorización
- Pasos para resolver ecuaciones cuadráticas completando el cuadrado
- Pasos para resolver ecuaciones cuadráticas con la fórmula cuadrática
- Ejercicios resueltos de ecuaciones cuadráticas
- Ejercicios de ecuaciones cuadráticas para resolver
- Véase también
Pasos para resolver ecuaciones cuadráticas incompletas
Las ecuaciones cuadráticas incompletas son ecuaciones que tienen un término faltante en la forma $latex ax^2+bx+c$. Dependiendo del término faltante, tenemos dos tipos de ecuaciones cuadráticas incompletas.
Resolver ecuaciones cuadráticas que no tienen el término bx
Las ecuaciones cuadráticas que no tienen el término bx tienen la forma $latex ax^2+c=0$. Para resolver estas ecuaciones, seguimos los siguientes pasos:
Paso 1: Simplificar la ecuación de ser posible.
Paso 2: Escribir a la ecuación de la siguiente forma:
$latex ax^2=-c$
Paso 3: Despejar a x² completamente. Para esto, dividimos a la ecuación por a. Muchas veces, el valor de a es 1, por lo que no tenemos que aplicar este paso.
$latex x^2=-\frac{c}{a}$
Paso 4: Sacamos la raíz cuadrada de ambos lados:
$latex x=\pm\sqrt{-\frac{c}{a}}$
Nota: Tanto la solución positiva como negativa deben ser consideradas porque $latex (-a)^2=a^2$.
Resolver ecuaciones cuadráticas que no tienen el término c
Las ecuaciones cuadráticas incompletas que no tienen el término c tienen la forma $latex ax^2+bx=0$. Para resolver estas ecuaciones, podemos seguir los siguientes pasos:
Paso 1: Simplificar la ecuación si es que es posible.
Paso 2: Factorizar la x del lado izquierdo de la ecuación:
$latex x(ax+b)=0$
Paso 3: Formar una ecuación con cada factor:
$latex x=0~~$ y $latex ~~ax+b=0$
Paso 4: Resolver las ecuaciones:
$latex x=0~~$ o $latex ~~x=-\frac{b}{a}$
Nota: Una de las soluciones siempre será $latex x=0$.
Pasos para resolver ecuaciones cuadráticas por factorización
Factorizar una ecuación cuadrática consiste en encontrar dos factores de la ecuación para escribirla en la forma $latex (x+p)(x+q)=0$. De esta forma, podremos fácilmente identificar las raíces de la ecuación cuadrática.
Para resolver ecuaciones cuadráticas por factorización, tenemos que seguir los siguientes pasos:
Paso 1: Simplifica si es que es posible y escribir a la ecuación en la forma $latex ax^2+bx+c=0$.
Paso 2: Usa cualquier método para factorizar a la ecuación cuadrática y escribirla en la forma $latex (x+p)(x+q)=0$.
Paso 3: Obtén una ecuación con cada factor al igualarlo a cero. Por ejemplo $latex x+p=0$.
Paso 4: Resuelve ambas ecuaciones lineales de los factores.
Recordemos que para factorizar una ecuación cuadrática tenemos que transformar a la ecuación de la forma $latex x^2+bx+c=0$ a la forma $latex (x+p)(x+q)=0$. Para lograr esto, tenemos que encontrar dos factores, los cuales al ser multiplicados, resulten en la ecuación cuadrática original.
Por ejemplo, la ecuación $latex x^2+2x-3=0$ puede ser factorizada en la forma $latex (x+3)(x-2)=0$, ya que al multiplicar los factores, obtenemos la ecuación original.
Puedes hacer una revisión de los métodos de factorización de ecuaciones cuadráticas al visitar nuestro artículo: Factorización de Ecuaciones Cuadráticas.
Pasos para resolver ecuaciones cuadráticas completando el cuadrado
Completar el cuadrado es una técnica de factorización que consiste en transformar una ecuación cuadrática de la forma $latex ax^2+bx+c=0$ a la forma $latex (x-h)^2+k=0$. Esta técnica nos permite resolver ecuaciones que no pueden ser factorizadas fácilmente.
Paso 1: Simplifica y escribe a la ecuación en la forma $latex ax^2+bx+c=0$.
Paso 2: Si es que el coeficiente a es diferente de 1, dividimos a toda la ecuación por a para lograr que el coeficiente del término cuadrático sea igual a 1:
$latex x^2+bx+c=0$
Paso 3: Divide al coeficiente b por 2:
$$\left(\frac{b}{2}\right)$$
Paso 4: Eleva al cuadrado a la expresión del paso 3:
$$\left(\frac{b}{2}\right)^2$$
Paso 5: Suma y resta la expresión obtenida en el paso 4 a la ecuación obtenida en el paso 2:
$$x^2+bx+\left(\frac{b}{2}\right)^2-\left(\frac{b}{2}\right)^2+c=0$$
Paso 6: Factoriza la ecuación aplicando la identidad $latex x^2+2xy+y^2=(x+y)^2$:
$$\left(x+\frac{b}{2}\right)^2-\left(\frac{b}{2}\right)^2+c=0$$
Paso 7: Simplifica para obtener una ecuación de la siguiente forma:
$latex (x-h)^2+k=0$
Paso 8: Reorganiza a la ecuación de la siguiente forma:
$latex (x-h)^2=-k$
Paso 9: Saca la raíz cuadrada de ambos lados de la ecuación:
$latex x-h=\sqrt{-k}$
Paso 10: Resuelve para x:
$latex x=h\pm \sqrt{-k}$
Pasos para resolver ecuaciones cuadráticas con la fórmula cuadrática
La fórmula cuadrática nos permite encontrar ambas soluciones de cualquier ecuación cuadrática. Podemos usar este método cuando no es posible resolver ecuaciones cuadráticas por ningún otro método.
Para resolver ecuaciones cuadráticas usando la fórmula cuadrática general, podemos seguir los siguientes pasos:
Paso 1: Simplifica y escribe a la ecuación en la forma $latex a{{x}^2}+bx+c=0$.
Paso 2: Sustituye los coeficientes a, b y c en la fórmula cuadrática:
| $$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$$ |
Paso 3: Usa el signo ±. El resultado de la raíz cuadrada debe ser sumado y restado separadamente para obtener ambas soluciones de la ecuación.
Una ecuación cuadrática puede tener dos raíces reales, una raíz real repetida o ninguna raíz real. Esto depende del discriminante de la ecuación, el cual es el valor que va dentro del signo de raíz cuadrada, es decir, $latex b^2-4ac$.
Entonces, dependiendo del valor del discriminante, tenemos lo siguiente:
- Cuando $latex b^2-4ac>0$, la ecuación tiene dos raíces reales.
- Cuando $latex b^2-4ac<0$, la ecuación no tiene raíces reales.
- Cuando $latex b^2-4ac=0$, la ecuación tiene una raíz repetida.
Si es que el valor dentro de la raíz cuadrada es positivo, tendremos dos raíces reales. Si es que ese valor es negativo, no tendremos raíces reales (pero sí raíces imaginarias o complejas). Si es que ese valor es igual a cero, tenemos una sola raíz.
Para aprender cómo derivar la fórmula cuadrática general, puedes visitar nuestro artículo Fórmula Cuadrática General – Derivación.
Ejercicios resueltos de ecuaciones cuadráticas
Los siguientes ejercicios son resueltos usando los métodos vistos arriba. Cada ejercicio tiene su respectiva solución, pero intenta resolver los ejercicios tú mismo antes de mirar la respuesta.
EJERCICIO 1
Encuentra las soluciones de la ecuación $latex x^2-36=0$.
Solución
Esta ecuación es una ecuación cuadrática incompleta que no tiene el término bx. Entonces, podemos resolverla al despejar al término x² y sacar la raíz cuadrada de ambos lados:
$latex x^2-36=0$
$latex x^2=36$
$latex x=\pm\sqrt{36}$
$latex x=\pm 6$
Las soluciones de la ecuación son $latex x=6$ y $latex x=-6$.
EJERCICIO 2
Encuentra las soluciones de la ecuación $latex 2x^2-9x=0$.
Solución
Esta ecuación es una ecuación cuadrática incompleta que no tiene el término c. Podemos resolverla al factorizar la x y formar una ecuación con cada factor:
$latex 2x^2-9x=0$
$latex x(2x-9)=0$
$latex x=0 ~~$ o $latex ~~2x-9=0$
$latex x=0 ~~$ o $latex ~~x=\frac{9}{2}$
Las soluciones de la ecuación son $latex x=0$ y $latex x=\frac{9}{2}$
EJERCICIO 3
Aplica el método de factorización para resolver la ecuación $latex x^2+2x-15=0$.
Solución
Podemos factorizar a la ecuación de la siguiente forma:
$latex x^2+2x-15=0$
$latex (x+5)(x-3)=0$
Formando una ecuación con cada factor y resolviendo, tenemos:
$latex x+5=0~~$ o $latex ~~x-3=0$
$latex x=-5~~$ o $latex ~~x=3$
Las soluciones de la ecuación son $latex x=-5$ y $latex x=3$.
EJERCICIO 4
Encuentra las soluciones de la ecuación $latex 2x^2-3x-20=0$ usando el método de factorización.
Solución
Factorizando el lado izquierdo de la ecuación, tenemos:
$latex 2x^2-3x-20=0$
$latex (2x+5)(x-4)=0$
Formando una ecuación con cada factor y resolviendo, tenemos:
$latex 2x+5=0~~$ o $latex ~~x-4=0$
$latex x=-\frac{5}{2}~~$ o $latex ~~x=4$
Las soluciones de la ecuación son $latex x=-\frac{5}{2}$ y $latex x=4$.
EJERCICIO 5
Resuelve la ecuación $latex x^2-3x+1=0$ usando el método de completar el cuadrado.
Solución
El coeficiente b de esta ecuación cuadrática es -3. Entonces, tenemos:
$$\left(\frac{b}{2}\right)^2=\left(\frac{-3}{2}\right)^2$$
Al sumar y restar esta expresión a la ecuación cuadrática original, tenemos:
$$x^2-3x+1=x^2-2x+\left(\frac{-3}{2}\right)^2-\left(\frac{-3}{2}\right)^2+1$$
Ahora, podemos completar el cuadrado y simplificar:
$latex = (x-\frac{3}{2})^2-\left(\frac{-3}{2}\right)^2+1$
$latex = (x-\frac{3}{2})^2-\frac{5}{4}$
Reorganizamos a la ecuación de la siguiente forma:
$latex ⇒ (x-\frac{3}{2})^2=\frac{5}{4}$
Sacando la raíz cuadrada de ambos lados, tenemos:
⇒ $latex x-\frac{3}{2}=\sqrt{\frac{5}{4}}$
⇒ $latex x-\frac{3}{2}=\frac{\sqrt{5}}{2}$
Resolviendo, tenemos:
⇒ $latex x=\frac{3}{2}\pm \frac{\sqrt{5}}{2}$
EJERCICIO 6
Resuelve la ecuación $latex 2x^2+8x-10=0$ usando el método de completar el cuadrado.
Solución
En este caso, tenemos que empezar dividiendo a toda la ecuación por 2 para lograr que el coeficiente del término cuadrático sea igual a 1:
⇒ $latex x^2+4x-5=0$
El coeficiente b de la ecuación cuadrática simplificada es igual a 4. Entonces, tenemos:
$$\left(\frac{b}{2}\right)^2=\left(\frac{4}{2}\right)^2$$
$$=2^2$$
Ahora, vamos a sumar y restar ese valor de la ecuación para obtener:
$$x^2+4x-5=x^2+4x+2^2-2^2-5$$
Cuando completamos el cuadrado y simplificamos, tenemos:
$latex = (x+2)^2-4-5$
$latex = (x+2)^2-9$
Ahora, reorganizamos a la ecuación de la siguiente manera:
⇒ $latex (x+2)^2=9$
Y sacamos la raíz cuadrada de ambos lados:
⇒ $latex x+2=\pm 3$
Resolviendo, tenemos:
⇒ $latex x=1$, $latex x=-5$
EJERCICIO 7
Encuentra las soluciones a la ecuación $latex 3x^2+x-3=0$ usando la fórmula cuadrática. Usa dos lugares decimales.
Solución
Podemos identificar los valores $latex a=3$, $latex b=1$ y $latex c=-3$. Entonces, al sustituir esos valores en la fórmula general, tenemos:
$$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$$
$$x=\frac{-(1)\pm \sqrt{( 1)^2-4(3)(-3)}}{2(3)}$$
$$=\frac{-1\pm \sqrt{1+36}}{6}$$
$$=\frac{-1\pm \sqrt{37}}{6}$$
$$x=-1.18\text{ o }0.85$$
Las soluciones de la ecuación son $latex x=-1.18$ y $latex x=0.85$.
Ejercicios de ecuaciones cuadráticas para resolver
Usa los métodos estudiados arriba para resolver las siguientes ecuaciones cuadráticas.
Véase también
¿Interesado en aprender más sobre ecuaciones cuadráticas? Puedes mirar estas páginas: