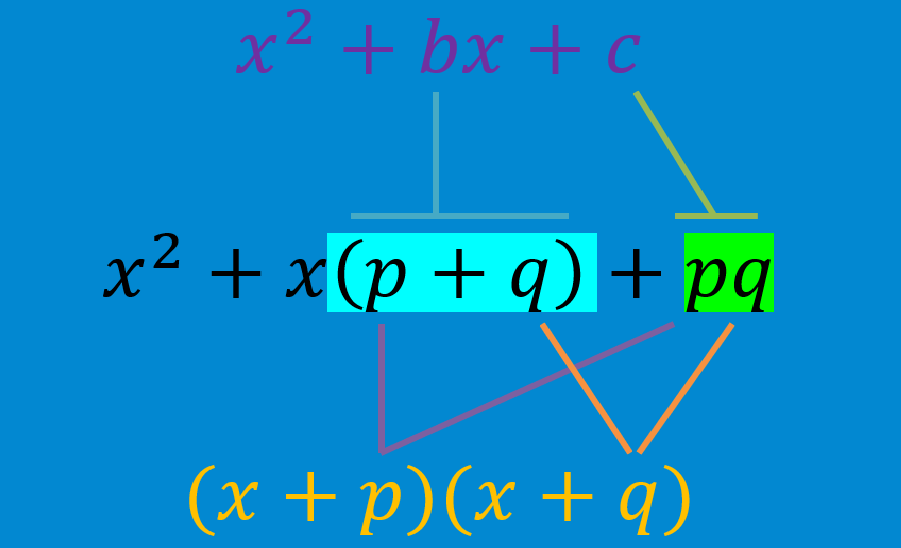La factorización de ecuaciones cuadráticas consiste en descomponer a la ecuación cuadrática y formar un producto de sus factores. La factorización puede ser considerada como el proceso reverso de la distribución de la multiplicación.
A continuación, aprenderemos sobre dos casos de factorización de ecuaciones cuadráticas. El primer caso se trata de ecuaciones cuadráticas con un coeficiente líder de 1 y el segundo caso se trata de ecuaciones cuadráticas con un coeficiente líder que es mayor que 1.
Resolver ecuaciones cuadráticas por factorización
Podemos usar la factorización para resolver ecuaciones cuadráticas que tienen la forma general $latex a{{x}^2}+bc+c=0$ con los siguientes pasos:
Paso 1: Simplificar la ecuación. Esto incluye eliminar paréntesis y fracciones si es que es necesario.
Paso 2: Ubicar a todos los términos en el lado izquierdo de la ecuación si es que no lo están.
Paso 3: Obtén la factorización de la ecuación al separar el término del medio.
Paso 4: Cada factor contiene a una solución.
EJEMPLO 1
Resuelve la ecuación cuadrática $latex 3({{x}^2}-2)=-3x$.
Solución: Tenemos que eliminar los paréntesis y mover a todos los términos hacia la izquierda de la ecuación:
$latex 3({{x}^2}-2)=-3x$
⇒ $latex 3{{x}^2}-6=-3x$
⇒ $latex 3{{x}^2}-3x-6=0$
Ahora, factorizamos la ecuación separando al término del medio (aprenderemos estos métodos más adelante):
⇒ $latex 3{{x}^2}-3x-6=0$
⇒ $latex (x+2)(3x-3)=0$
Ahora, podemos encontrar la respuesta de cada factor:
⇒ $latex (x+2)=0$ y $latex (3x-3)=0$
⇒ $latex x=-2$ y $latex x=1$
EJEMPLO 2
Resuelve la ecuación cuadrática $latex 3{{x}^2}-8x-5=0$.
Solución: Aquí no tenemos nada para simplificar y todos los términos ya están en la izquierda. Entonces, tenemos que separar los términos del medio para factorizar (veremos estos métodos más adelante):
$latex 3{{x}^2}-8x-5=0$
⇒ $latex 3x(x-3)+1(x-3)=0$
⇒ $latex (3x+1)(x-3)=0$
Ahora, podemos resolver para cada factor:
⇒ $latex (3x+1)=0$ y $latex (x-3)=0$
⇒ $latex x=-\frac{1}{3}$ y $latex x=3$
EJEMPLO 3
Resuelve la ecuación ecuadrática $latex {{(2x-3)}^2}=25$.
Solución: Tenemos que aplicar el exponente para eliminar el paréntesis y simplficar. También, movemos todos los términos hacia la izquierda:
$latex 4{{x}^2}-12x+9-25=0$
⇒ $latex 4{{x}^2}-12x-16=0$
Simplificamos al dividir toda la ecuación por 4 y factorizamos:
⇒ $latex {{x}^2}-3x-4=0$
⇒ $latex (x-4)(x+1)=0$
Resolvemos en cada factor:
⇒ $latex (x-4)=0$ y $latex (x+1)=0$
⇒ $latex x=4$ y $latex x=-1$
Existen diferentes métodos que pueden ser usados para factorizar ecuaciones cuadráticas. Nuestro enfoque aquí será aprender a factorizar ecuaciones cuadráticas en las cuales el coeficiente de x² es o bien 1 o mayor que 1.
Aprenderemos a factorizar usando el método de prueba y error, el cual nos permitirá obtener los factores correctos para factorizar las ecuaciones cuadráticas.
Factorización de ecuaciones cuadráticas cuando el coeficiente de x² es igual a 1
Este es el caso más fácil de factorización de ecuaciones cuadráticas. Para factorizar ecuaciones cuadráticas de la forma $latex {{x}^2}+bx+c$, en donde el coeficiente líder es 1, tenemos que encontrar dos números de forma que al multiplicarlos, obtengamos la constante c y al sumarlos, obtengamos el coeficiente b.
Primer caso: Cuando b y c son ambos positivos
EJEMPLO 1
Factoriza y obtén la solución a la ecuación cuadrática $latex {{x}^2}+6x+8=0$.
Solución: Podemos formar una lista con los factores de 8: 1×8, 2×4.
Tenemos que encontrar los factores que tienen una suma de 6 y un producto de 8:
1+8≠6
2+4=6
Podemos verificar estos factores usando la propiedad distributiva:
$$(x+2)(x+4)={{x}^2}+2x+4x+8$$
$latex ={{x}^2}+6x+8$
Entonces, ya hemos factorizado a la ecuación:
$latex (x+2)(x+4)=0$
Ahora, resolvemos para cada factor:
⇒ $latex (x+2)=0$ y $latex (x+4)=0$
⇒ $latex x=-2$ y $latex x=-4$
EJEMPLO 2
Resuelve la ecuación $latex {{x}^2}+8x+15=0$ usando factorización.
Solución: Los factores con un producto de 15 y una suma 8 son:
3×5=15 y 3+5=8
Usamos la propiedad distributiva para verificar:
$$(x+3)(x+5)={{x}^2}+3x+5x+15$$
$latex ={{x}^2}+8x+15$
La ecuación factorizada es:
$latex (x+3)(x+5)=0$
Resolvemos cada factor:
⇒ $latex (x+3)=0$ y $latex (x+5)=0$
⇒ $latex x=-3$ y $latex x=-5$
Segundo caso: Cuando b es positivo y c es negativo
EJEMPLO
Resuelve la ecuación $latex {{x}^2}+6x-7=0$ por factorización.
Solución: Los factores de -7 son: -1×7, 1×-7.
Encontramos los factores con un producto de -7 y una suma de 6:
-1+7=6
1-7≠6
Verificamos con la propiedad distributiva:
$latex (x-1)(x+7)={{x}^2}-x+7x-7$
$latex ={{x}^2}+6x-7$
Ya hemos obtenido la factorización de la ecuación:
$latex (x-1)(x+7)=0$
Resolvemos para cada factor:
⇒ $latex (x-1)=0$ y $latex (x+7)=0$
⇒ $latex x=1$ y $latex x=-7$
Tercer caso: Cuando b y c son ambos negativos
EJEMPLO
Factoriza y resuelve la ecuación $latex {{x}^2}-3x-10=0$.
Solución: Los factores de -10 son: -1×10, 1×-10, -2×5, 2×-5.
Identificamos los factores que produzcan un producto de -10 y una suma de -3:
2-5=-3
Usando la propiedad distributiva, podemos verificar los factores:
$$(x+2)(x-5)={{x}^2}+2x-5x-10$$
$latex ={{x}^2}-3x-10$
Entonces, la factorización de la ecuación es:
$latex (x+2)(x-5)=0$
Resolvemos a cada factor:
⇒ $latex (x+2)=0$ y $latex (x-5)=0$
⇒ $latex x=-2$ y $latex x=5$
Cuarto caso: Cuando b es negativo y c es positivo
EJEMPLO
Resuelve la ecuación $latex {{x}^2}-9x+14=0$ por factorización.
Solución: Empezamos encontrando los factores de 14: -1×-14, -2×-7.
Los factores con un producto de 14 y una suma de -9 son:
-2-7=-9
-1-14≠-9
Verificando con la propiedad distributiva, tenemos:
$$(x-2)(x-7)={{x}^2}-2x-7x+14$$
$latex ={{x}^2}-9x+14$
La factorización es:
$latex (x-2)(x-7)=0$
Resolviendo para cada factor, tenemos:
⇒ $latex (x-2)=0$ y $latex (x-7)=0$
⇒ $latex x=2$ y $latex x=7$
Factorización de ecuaciones cuadráticas cuando el coeficiente de x² es mayor que 1
Los métodos que acabamos de ver no funcionan cuando el coeficiente líder es diferente de 1. Para estos casos, tenemos que tener en cuenta el coeficiente de $latex {{x}^2}$ y los factores de c para encontrar números que tienen una suma igual a b.
EJEMPLO 1
Resuelve la ecuación $latex 2{{x}^2}-16x+30=0$ por factorización.
Solución: Tenemos que determinar si es que hay factores comunes en la expresión. En este caso, podemos extraer el 2:
⇒ $latex 2({{x}^2}-8x+15)=0$
Podemos factorizar a $latex ({{x}^2}-8x+15)$. Los factores de 15 son: -1×-15 , -3×-5.
Determinamos cuáles factores producen una suma de -8:
-3-5=-8
-1-15≠-8
Usamos la propiedad distributiva para verificar:
$$2(x-3)(x-5)=2({{x}^2}-3x-5x+15)$$
$latex =2({{x}^2}-8x+15)$
$latex =2{{x}^2}-16x+30$
La ecuación factorizada es:
$latex 2(x-3)(x-5)=0$
Resolvemos para cada factor:
⇒ $latex (x-3)=0$ y $latex (x-5)=0$
⇒ $latex x=3$ y $latex x=5$
EJEMPLO 2
Factoriza y resuelve la ecuación cuadrática $latex 7{{x}^2}+18x+11=0$.
Solución: Tenemos que encontrar los factores de 7 y 11:
1×7=7
1×11=11
Ahora, usamos la la propiedad distributiva para verificar los factores:
$$(7x+1)(x+11)\ne 7{{x}^2}+18x+11$$
$$(7x+11)(x+1)=7{{x}^2}+18x+11$$
La factorización de la ecuación cuadrática es:
$latex (7x+11)(x+1)=0$
Resolvemos para cada factor:
⇒ $latex (7x+11)=0$ y $latex (x+1)=0$
⇒ $latex x=-\frac{11}{7}$ y $latex x=-1$
EJEMPLO 3
Obtén la factorización y resuelve la ecuación $latex 9{{x}^2}+6x+1=0$.
Solución: Usando el mismo proceso de los anteriores ejercicios, podemos obtener la factorización de la ecuación cuadrática:
$latex (3x+1)(3x+1)=0$
Resolvemos para cada factor:
⇒ $latex (3x+1)=0$ y $latex (3x+1)=0$
⇒ $latex x=-\frac{1}{3}$
EJEMPLO 4
Resuelve la ecuación $latex 6{{x}^2}-7x+2=0$ por factorización.
Solución: En este caso, es conveniente que empecemos separando el término del medio:
$latex 6{{x}^2}-4x-3x+2=0$
Siguiendo el mismo proceso de los ejercicios anteriores, tenemos:
$latex 2x(3x-2)-1(3x-2)=0$
$latex (3x-2)(2x-1)=0$
Resolviendo para cada factor, tenemos:
⇒ $latex (3x-2)=0$ y $latex (2x-1)=0$
⇒ $latex x=\frac{2}{3}$ y $latex x=\frac{1}{2}$
Véase también
¿Interesado en aprender más sobre factorización? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
