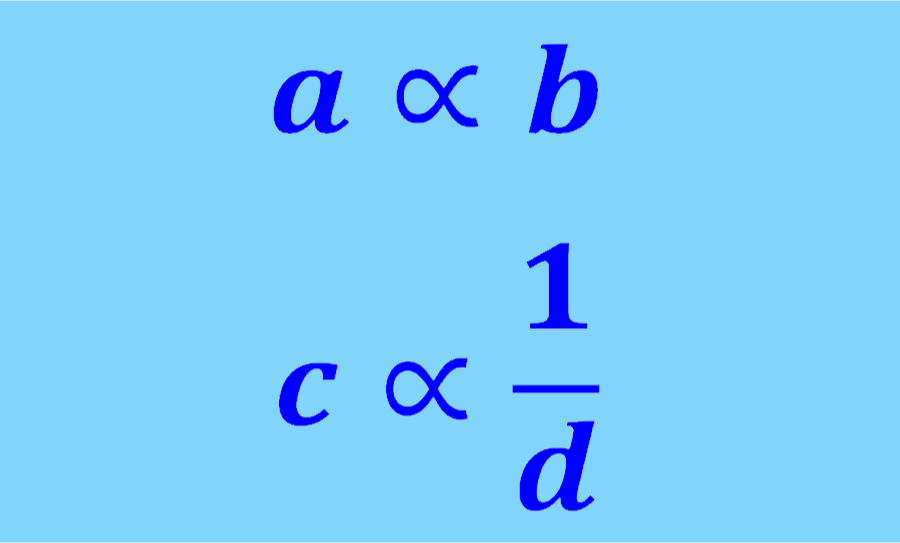La proporcionalidad directa e inversa nos permite comparar dos cantidades y entender cómo se relacionan. Cuando dos cantidades son directamente proporcionales, al incrementar una cantidad, la otra cantidad también incrementa. Cuando dos cantidades son inversamente proporcionales, al incrementar una cantidad, la otra cantidad disminuye.
En este artículo, miraremos la proporcionalidad directa y la proporcionalidad inversa detalladamente. También, aprenderemos sobre la regla del 3, la cual nos permite resolver problemas de proporcionalidad fácilmente.
Proporcionalidad directa e inversa definiciones
La proporcionalidad directa e inversa es usada para mostrar cómo dos cantidades se relacionan la una con la otra. El símbolo usado para denotar la proporcionalidad es “∝”. Por ejemplo, si es que decimos que a es proporcional a b, esto es representado por “a∝b“.
Si es que decimos que a es inversamente proporcional a b, esto es denotado como “a∝1/b“. Estas relaciones están gobernadas por las mismas reglas de probabilidad. En ambos casos, el valor de a cambia cuando b cambia o el valor de b cambia cuando a cambia.
El cambio en ambos valores está igualado con una constante de proporcionalidad. Veremos ejemplos más adelante para entender esto completamente.
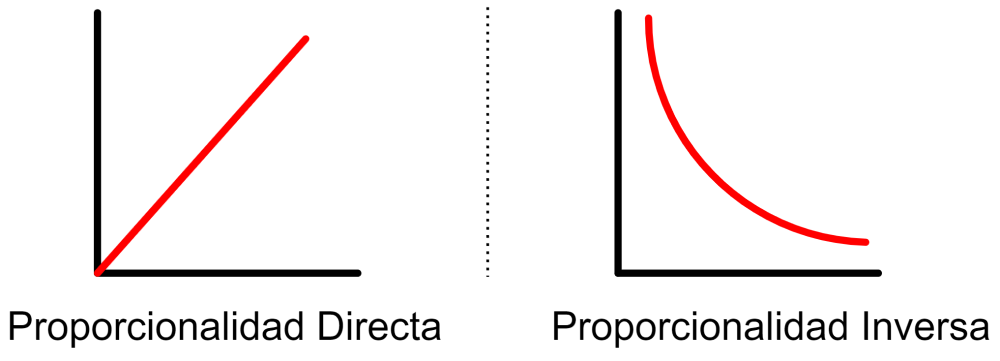
Proporcionalidad directa
Dos cantidades a y b tienen una proporcionalidad directa si es que incrementan o decrecen juntas, es decir, la razón de sus valores correspondientes permanece constante. Esto significa que tenemos:
$latex \frac{a}{b}=k$
en donde k es un número positivo, entonces las variables a y b están variando directamente.
El símbolo usado para representar la proporción directa es “∝”.
Supongamos que a es proporcional a b. Esto puede ser escrito como:
a∝b
EJEMPLO
Supongamos que tenemos $latex a=3b$. Esto muestra que a es proporcional a b y el valor de una variable puede ser encontrado si es que conocemos el valor de la otra variable.
Si tenemos que el valor de b es 5, $latex b=5$, entonces tenemos:
$latex a=3(5)=15$
De igual forma, si tenemos que el valor de a es 15, podemos encontrar el valor de b:
$latex 15=3b$
$latex b=5$
Regla del 3 directa
La regla del 3 es una operación que nos ayuda a resolver problemas de proporcionalidad directa e inversa rápidamente.
Para poder usar la regla del 3, necesitamos tres valores: dos que son proporcionales el uno con el otro y un tercero. Con estos valores, podemos encontrar un cuarto.
Veamos el caso de proporciones directas. Vamos a colocar los tres valores a, b, c y el valor desconocido x de la siguiente manera y luego aplicaremos la fórmula:
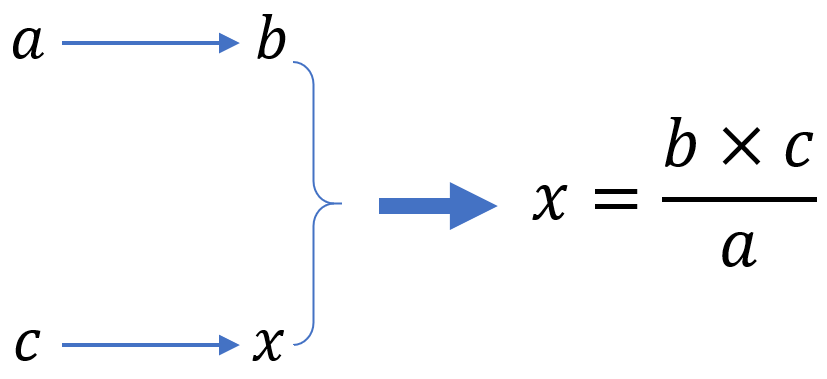
EJEMPLO
Felipe es un albañil y construye casas. Él dice que para construir 2 casas se tarda 11 meses. Hoy recibió una oferta para construir 5 casas. ¿Cuántos meses le tomaría para construir las 5 casas?
Solución: Formemos una tabla con los valores que conocemos y encontraremos el valor desconocido usando la fórmula:
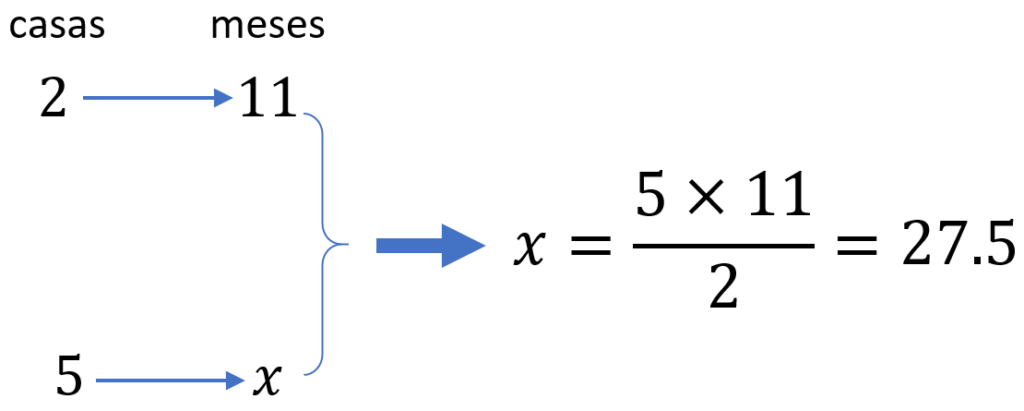
Entonces, le tomará 27.5 meses para construir 5 casas.
Inténtalo tú mismo – Resuelve el ejercicio
Proporcionalidad inversa
Dos valores son inversamente proporcionales cuando un valor incrementa mientras el otro decrece. Por ejemplo, a y b son inversamente proporcionales si es que cuando a incrementa, b decrece y viceversa. Esto significa que el producto de sus valores correspondientes debe permanecer constante. Es decir, si es que $latex ab=k$, entonces a y b son inversamente proporcionales.
El símbolo de probabilidad es usado en una forma distinta. Lo siguiente nos dice que a es inversamente proporcional a b:
a∝$latex \frac{1}{b}$
EJEMPLO
Supongamos que tenemos $latex a=\frac{2}{b}$. Esto muestra que a es inversamente proporcional a b y el valor de una variable puede ser encontrado si es que conocemos el valor de la otra variable.
Si tenemos que el valor de b es 4, $latex b=4$, entonces tenemos:
$latex a=\frac{2}{4}=\frac{1}{2}$
De igual forma, si tenemos que el valor de a es 6, podemos encontrar el valor de b:
$latex 6=\frac{1}{b}$
$latex b=\frac{1}{6}$
Regla del 3 inversa
Ahora veamos cómo aplicar la regla del 3 en el caso de proporcionalidad inversa. Colocaremos los 3 valores conocidos en la tabla similar al caso anterior, pero usaremos una fórmula distinta:
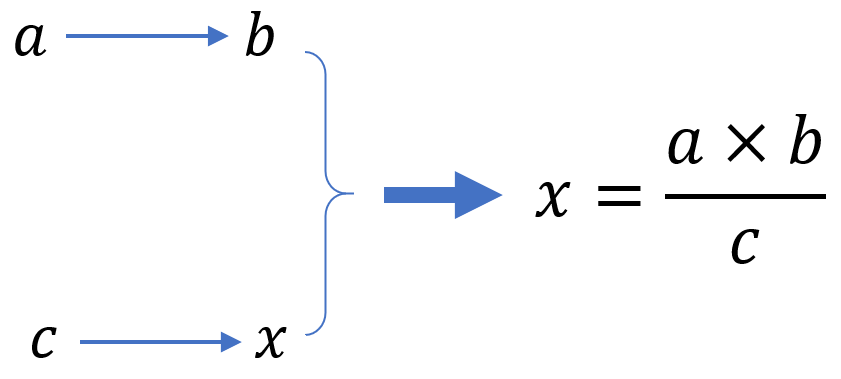
EJEMPLO
En una bodega están transportando grandes cantidades de arroz. Usando 4 camiones, les tomaría 10 viajes cada uno para trasportar toda la mercancía. Si es que usan 5 camiones, ¿cuántos viajes les tomaría a cada uno para transportar esa mercancía?
Solución: Vamos a formar una tabla con los valores que conocemos y usaremos la fórmula para obtener el valor desconocido:
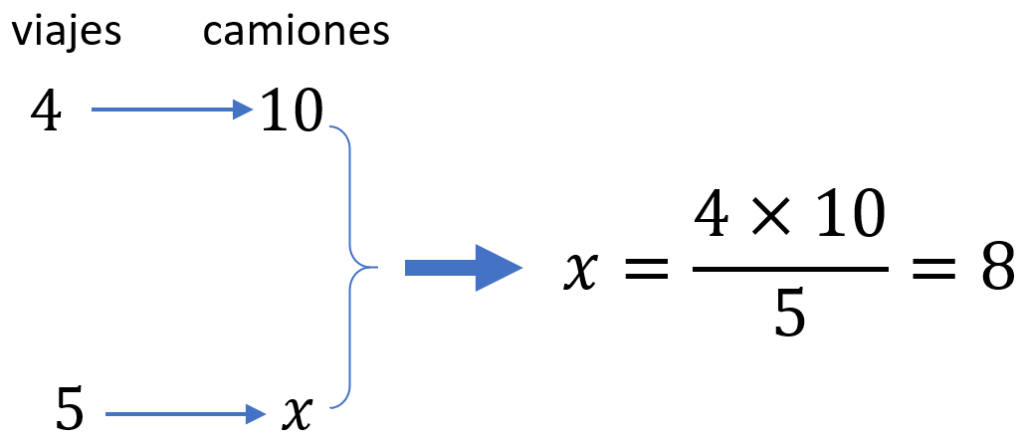
Entonces, usando 5 camiones, les tomaría 8 viajes a cada uno para transportar toda la mercancía.
Inténtalo tú mismo – Resuelve el ejercicio
Véase también
¿Interesado en aprender más sobre otros temas algebraicos? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
