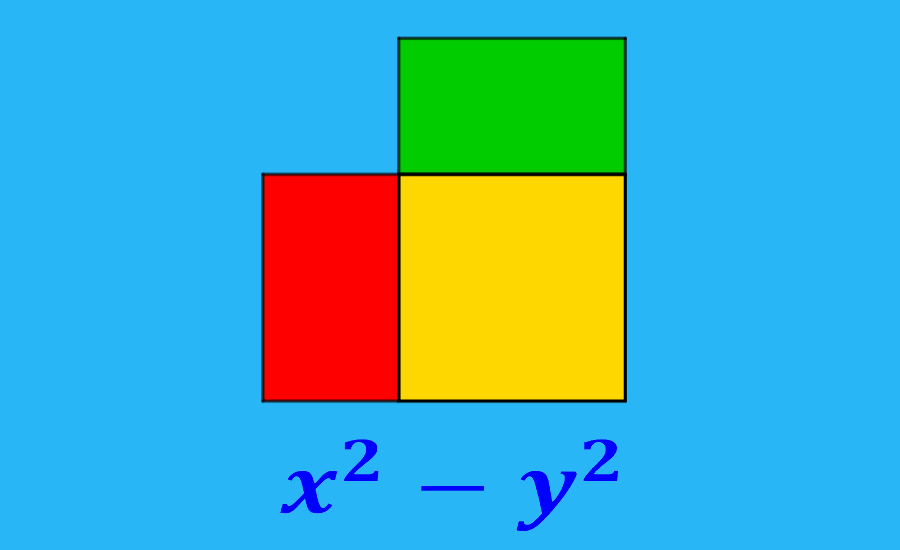Cuando aprendemos a factorizar, usualmente exploramos fórmulas importantes al mismo tiempo. Una de estas fórmulas es la diferencia de cuadrados. El teorema de la diferencia de cuadrados nos dice que si es que tenemos una expresión de la forma a²-b², esto es equivalente a (a+b)(a–b).
En este artículo, aprenderemos qué es la diferencia de cuadrados, miraremos cómo factorizar usando esta fórmula y veremos ejemplos resueltos para entender los conceptos.
¿Qué es la diferencia de cuadrados?
La diferencia de dos cuadrados es un teorema que nos dice si es que una ecuación cuadrática puede ser escrita como un producto de dos binomios, en donde uno muestra la diferencia de las raíces cuadradas y el otro muestra la suma de las raíces cuadradas.
Una diferencia de cuadrados es algo que se ve como $latex x^2-4$. Esto es debido a que $latex 2^2=4$, por lo que en realidad tenemos $latex x^2-2^2$, algo que es una diferencia de cuadrados.
Diferencia de cuadrados fórmula
La fórmula de la diferencia de cuadrados es una forma algebraica que es usada para expresar la diferencia entre dos valores elevados al cuadrado. Una diferencia de cuadrados es expresada en la forma:
$latex a^2-b^2$
en donde el primero y el último término son cuadrados perfectos.
Factorizando la diferencia de cuadrados, tenemos:
$latex a^2-b^2=(a+b)(a-b)$
Esto es verdadero debido a que $$(a+b)(a-b)=a^2+ab-ab-b^2=a^2-b^2$$
¿Cómo factorizar la diferencia de cuadrados?
Los siguientes son los pasos requeridos para factorizar una diferencia de cuadrados:
1. Factoriza la expresión inicial si es posible.
Determina si es que los términos tienen un factor común. Si es que es así, factoriza ese factor común y no olvides incluirlo en la respuesta final. Por ejemplo, $latex 2x^2-32=2(x^2-16)$.
2. Aplica la fórmula de la diferencia de cuadrados.
La fórmula de la diferencia de cuadrados es $latex a^2-b^2=(a+b)(a-b)$. Por ejemplo, $latex 2(x^2-16)$ es igual a $latex 2(x+4)(x-4)$.
3. Factoriza y simplifica el resultado final.
Determina si es que los factores restantes pueden ser factorizados aún más o simplificados.
Ejemplos resueltos
EJEMPLO 1
Factoriza $latex {{x}^{2}}-9$.
Solución
Paso 1: En este caso, la expresión no necesita ser factorizada.
Paso 2: Para factorizar al problema en la forma $latex (a+b)(a-b)$ necesitamos determinar el valor al que tenemos que elevar al cuadrado para obtener $latex {{x}^{2}}$ y el valor al que tenemos que elevar al cuadrado para obtener 9.
En este caso, tenemos x y 3, ya que $latex (x)(x)={{x}^{2}}$ y $latex (3)(3)=9$.
$latex {{x}^{2}}-9$
$latex =(x+3)(x-3)$
Paso 3: La expresión ya está en su forma más simple.
EJEMPLO 2
Usa la diferencia de cuadrados para factorizar $latex 4x^2-49$.
Solución
Paso 1: Los términos no tienen un factor común.
Paso 2: Para factorizar al problema en la forma $latex (a+b)(a-b)$ necesitamos determinar el valor al que tenemos que elevar al cuadrado para obtener $latex 4x^2$ y al valor que tenemos que elevar al cuadrado para obtener 49.
En este caso, tenemos 2x y 7 porque $latex (2x)(2x)=4x^2$ y $latex (7)(7)=49$.
$latex 4x^2-49$
$latex =(2x+7)(2x-7)$
Paso 3: La expresión ya está en su forma más simple.
EJEMPLO 3
Factoriza la expresión $latex 18x^2-98$.
Solución
Paso 1: Los términos tienen un factor común:
$latex 2(9x^2-49)$
Paso 2: Necesitamos determinar el valor al que tenemos que elevar al cuadrado para obtener $latex 9x^2$ y el valor al que tenemos que elevar al cuadrado para obtener 49.
En este caso, tenemos 3x y 7 porque $latex (3x)(3x)=3x^2$ y $latex (7)(7)=49$.
$latex 2(9x^2-49)$
$latex =2(3x+7)(3x-7)$
Paso 3: La expresión ya está en su forma más simple.
EJEMPLO 4
Usa la diferencia de cuadrados en la expresión $latex 4x^2-64$.
Solución
Paso 1: Los términos tienen un factor común.
$latex 4(x^2-16)$
Paso 2: Tenemos que encontrar el valor al que tenemos que elevar al cuadrado para obtener $latex x^2$ y el valor que tenemos que elevar al cuadrado para obtener 16.
Entonces, tenemos x y 4 porque $latex (x)(x)=x^2$ y $latex (4)(4)=16$.
$latex 4(x^2-16)$
$latex =4(x+4)(x-4)$
Paso 3: El resultado ya no puede ser simplificado.
EJEMPLO 5
Factoriza la expresión $latex 16x^4-1$.
Solución
Paso 1: No tenemos factores comunes.
Paso 2: Tenemos que encontrar el valor al que tenemos que elevar al cuadrado para obtener $latex 16x^4$ y el valor al que tenemos que elevar al cuadrado para obtener 1.
En este caso, tenemos $latex 4x^2$ y 1 porque $latex (4x^2)(4x^2)=16x^4$ y $latex (1)(1)=1$.
$latex (4x^2+1)(4x^2-1)$
Paso 3: Uno de los factores es una diferencia de cuadrados, por lo que podemos factorizarlo: necesitamos determinar el valor al que tenemos que elevar al cuadrado para obtener $latex 4x^2$ y el valor al que tenemos que elevar al cuadrado para obtener 1.
En este caso, tenemos $latex 2x$ y 1 porque $latex (2x)(2x)=4x^2$ y $latex (1)(1)=1$.
$latex (4x^2+1)(2x+1)(2x-1)$
Si es que quieres explorar más ejemplos de diferencia de cuadrados, puedes visitar nuestro artículo: Ejercicios de Diferencia de Cuadrados.
Ejercicios de práctica de diferencia de cuadrados
Factoriza la expresión $latex 4x^2-36$ usando la diferencia de cuadrados.
Escribe la respuesta en la casilla.
Véase también
¿Interesado en aprender más sobre diferencia de cuadrados y otros temas algebraicos? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
