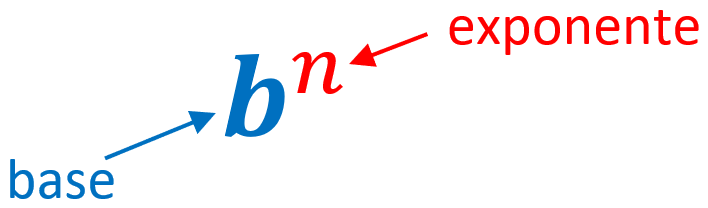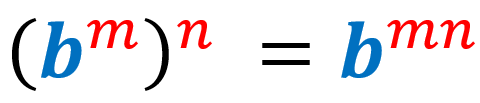Cuando tenemos la potencia de la potencia en expresiones exponenciales, encontramos la nueva potencia al multiplicar las dos potencias. Por ejemplo, en la siguiente expresión, x al cuadrado está siendo elevada a la potencia de 5, por lo que multiplicamos el 2 y el 5 para encontrar la nueva potencia.
$latex \left(x^2\right)^5=x^{(2)(5)}=x^{10}$
ÁLGEBRA
Relevante para…
Resolver ejercicios de expresiones con potencia de la potencia.
ÁLGEBRA
Relevante para…
Resolver ejercicios de expresiones con potencia de la potencia.
Regla de la potencia de la potencia
Recordemos que las expresiones exponenciales tienen dos partes. La primera parte es la base y la segunda es el exponente como puede verse en la ilustración:
- El exponente es el número que indica cuántas veces la base será multiplicada por sí misma.
- La base es el número o variable que está siendo multiplicada repetidamente.
La regla de la potencia de la potencia nos dice que, cuando tenemos una expresión exponencial elevada a una potencia, simplemente tenemos que copiar la base y multiplicar los exponentes. Aquí asumimos que la base es diferente de cero y los exponentes son números enteros:
Ejemplos resueltos
Los siguientes ejemplos nos muestran cómo podemos resolver expresiones en las que tenemos una potencia de la potencia:
EJEMPLOS 1
Cada factor dentro del paréntesis es elevado al exponente que está afuera del paréntesis:
- $latex {{\left( {{{3}^{4}}} \right)}^{5}}={{3}^{{\left( 4 \right)\left( 5 \right)}}}={{3}^{{20}}}$
- $latex {{\left( {{{4}^{{-2}}}} \right)}^{3}}={{4}^{{\left( {-2} \right)\left( 3 \right)}}}={{4}^{{-6}}}=\frac{1}{{{{4}^{6}}}}$
- $latex {{\left( {{{x}^{3}}} \right)}^{5}}={{x}^{{\left( 3 \right)\left( 5 \right)}}}={{x}^{{15}}}$
- $latex {{\left( {{{x}^{2}}{{y}^{4}}} \right)}^{3}}={{x}^{{\left( 2 \right)\left( 3 \right)}}}{{y}^{{\left( 4 \right)\left( 3 \right)}}}={{x}^{6}}{{y}^{{12}}}$
EJEMPLO 2
En el siguiente ejemplo, usamos el orden de las operaciones para resolver. Primero elevamos las expresiones dentro del paréntesis a sus potencias. Luego multiplicamos las dos expresiones. Aplicamos la regla del producto para simplificar las expresiones al combinar las bases iguales y sumar los exponentes:
$latex {{\left( {2{{x}^{2}}{{y}^{4}}} \right)}^{3}}{{\left( {4{{x}^{3}}{{y}^{2}}} \right)}^{2}}$
$latex =\left( {{{2}^{3}}{{x}^{{2\times 3}}}{{y}^{{4\times 3}}}} \right)\left( {{{4}^{2}}{{x}^{{3\times 2}}}{{y}^{{2\times 2}}}} \right)$
$latex =\left( {8{{x}^{6}}{{y}^{{12}}}} \right)\left( {16{{x}^{6}}{{y}^{4}}} \right)$
$latex =128{{x}^{{12}}}{{y}^{{16}}}$
EJEMPLOS 3
El siguiente ejemplo es similar al anterior, pero con exponentes negativos:
$latex {{\left( {{{x}^{2}}{{y}^{3}}} \right)}^{-3}}{{\left( {{{x}^{-3}}{{y}^{-4}}} \right)}^{-4}}$
$latex =\left( {{{x}^{{2\times -3}}}{{y}^{{3\times -3}}}} \right)\left( {{{x}^{{-3\times -4}}}{{y}^{{-4\times -4}}}} \right)$
$latex =\left( {{{x}^{-6}}{{y}^{{-9}}}} \right)\left( {{{x}^{12}}{{y}^{16}}} \right)$
$latex ={{x}^{{6}}}{{y}^{{7}}}$
Inténtalo tú mismo – Resuelve los ejercicios
Véase también
¿Interesado en aprender más sobre otros temas algebraicos? Mira estas páginas: