Las reglas de los exponentes son unas de las reglas en el álgebra con las que más tenemos que estar familiarizados. El dominio de las reglas de los exponentes básicas hará que tu estudio del álgebra sea más fácil y productivo. En este artículo, conoceremos todas las reglas de los exponentes y usaremos ejemplos para facilitar el dominio de estas reglas.
Partes de expresiones exponenciales
Empecemos explorando las partes de una expresión exponencial.
Una expresión exponencial está compuesta de dos partes. La primera parte es la base, la cual “lleva” al exponente, el cual es la segunda parte y está ubicada en la parte superior derecha, como puede verse en la ilustración:
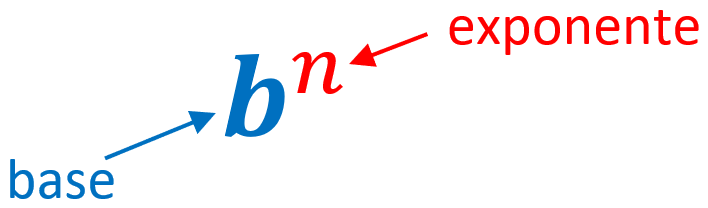
- El exponente es el número que indica cuántas veces la base será multiplicada por sí misma.
- La base es el número o variable que está siendo multiplicada repetidamente.
Por ejemplo, intentemos escribir $latex 3\times 3\times 3\times 3$ en notación de exponentes.
El número 3 es el número que está siendo multiplicado repetidamente, por lo que inmediatamente sabemos que el 3 es la base. Observamos que está escrito 4 veces. Este número indica el número de veces que la base está siendo multiplicada, por lo que sabemos que es el exponente.
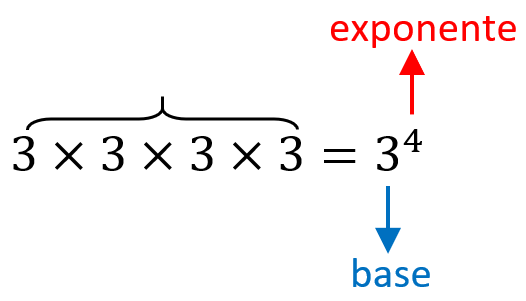
La base de una expresión algebraica también puede ser una letra o variable. Por ejemplo, si es que tenemos a la variable $latex x$ multiplicada repetidamente por sí misma, podemos escribirla en notación de exponentes:
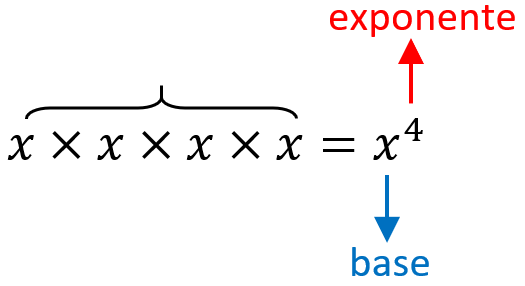
Resumen rápido de las reglas de los exponentes
En las siguientes reglas, a y b son números reales diferentes de cero y m y n son números enteros:
1) Regla del cero de exponentes:
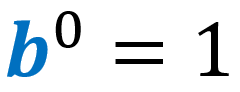
2) Regla de exponentes negativos:
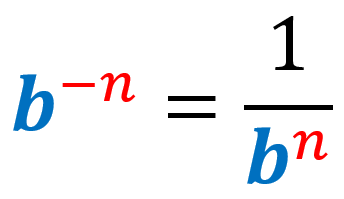
3) Regla del producto de exponentes:
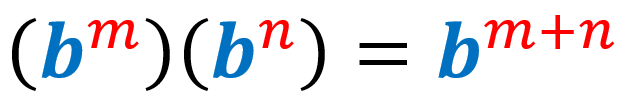
4) Regla del cociente de exponentes:
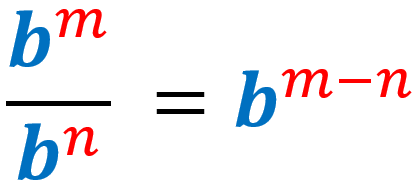
5) Potencia de una potencia de exponentes:
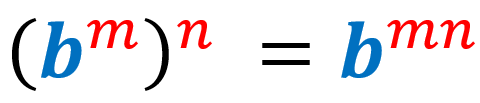
6) Potencia de un producto de exponentes:
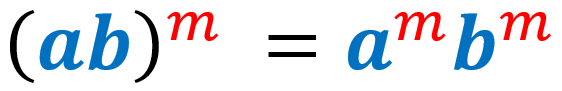
7) Potencia de un cociente de exponentes:
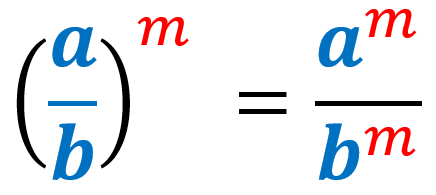
Descripción de las reglas de los exponentes con ejemplos
1) Regla del cero de exponentes
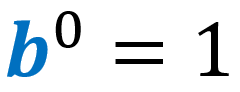
Cualquier número elevado a la potencia de cero es igual a 1.
EJEMPLOS
- Simplifica la expresión exponencial $latex {{4}^{0}}$.
Aquí, la base es 4 y el exponente es 0. Podemos aplicar la regla del cero directamente. Entonces, $latex {{4}^{0}}=1$.
- Simplifica la expresión exponencial $latex {{\left( {3x{{y}^{2}}} \right)}^{0}}$.
La base es toda la expresión que está dentro de los paréntesis. Esto es más fácil de lo que parece. Siempre y cuando las variables $latex x$ y $latex y$ sean diferentes de cero, la regla del cero aplica y tenemos $latex {{\left( {3x{{y}^{2}}} \right)}^{0}}=1$.
2) Regla de exponentes negativos
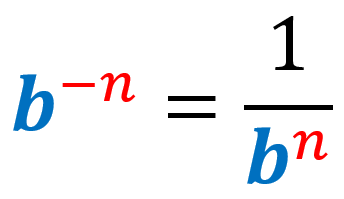
Cualquier número que está elevado a un exponente negativo no está en su forma estándar. Tendremos que reorganizarlo. Para lograr esto, movemos la base con el exponente negativo al lado opuesto de la fracción y luego hacemos positivo al exponente.
EJEMPLOS
- Simplifica la expresión exponencial $latex {{2}^{{-3}}}$.
Aquí, la base es 2 y tiene un exponente negativo de -3. Usando la regla de los exponentes negativos, podemos moverlo al denominador de la fracción y cambiar el exponente de negativo a positivo:
$latex {{2}^{{-3}}}=\frac{1}{{{{2}^{3}}}}$
$latex =\frac{1}{8}$
- Simplifica la expresión exponencial $latex \frac{1}{{{{x}^{-5}}}}$.
La base con exponente negativo está en el denominador. Podemos moverla al numerador y cambiar el exponente de negativo a positivo:
$latex \frac{1}{{{{x}^{-5}}}}={{x}^{{5}}}$
3) Regla del producto de exponentes
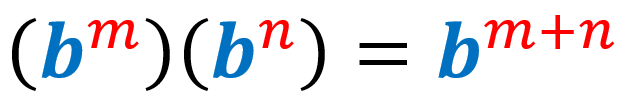
Cuando multiplicamos dos expresiones exponenciales, en donde tenemos la misma base, copiamos la base y sumamos sus exponentes. Aquí asumimos que la base b es diferente de cero y los exponentes m y n son números enteros.
EJEMPLOS
- Simplifica el producto de las expresiones exponenciales $latex ({{x}^{{3}}})({{x}^{{5}}})$.
Usando la regla del producto de exponentes, simplemente copiamos la base y sumamos los exponentes
$latex ({{x}^{{3}}})({{x}^{{5}}})={{x}^{{5+3}}}$
$latex ={{x}^{{8}}}$
- Simplifica el producto de las expresiones exponenciales $latex (2{{x}^{{2}}}{{y}^{{3}}})(3{{x}^{{3}}}{{y}^{{4}}})$.
En este caso, cada paréntesis contiene un número, la variable x y la variable y. Para resolver esto, tenemos que asegurarnos de multiplicar solo los términos del mismo tipo, es decir, multiplicamos los números y las variables separadamente:
$latex (2{{x}^{{2}}}{{y}^{{3}}})(3{{x}^{{3}}}{{y}^{{4}}})$
$latex =(2\times 3)({{x}^{{2}}}\times {{x}^{{3}}})({{y}^{{3}}}\times {{y}^{{4}}})$
$latex =6({{x}^{{2+3}}})({{y}^{{3+4}}})$
$latex =6({{x}^{{5}}})({{y}^{{7}}})$
4) Regla del cociente de exponentes
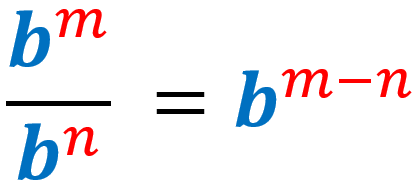
Cuando tenemos una división de expresiones exponenciales con la misma base, copiamos la base y restamos al exponente de la expresión del numerador por el exponente de la expresión del denominador.
Aquí asumimos que la base b es diferente de cero y los exponentes m y n son números enteros.
EJEMPLOS
- Simplifica la división de expresiones exponenciales $latex \frac{{{{x}^{4}}}}{{{{x}^{2}}}}$.
Aplicando la regla del cociente, copiamos la base y restamos el exponente de abajo al exponente de arriba:
$latex \frac{{{{x}^{4}}}}{{{{x}^{2}}}}={{{x}^{4-2}}}$
$latex ={{{x}^{2}}}$
- Simplifica la división de expresiones exponenciales $latex \frac{{{{x}^{3}}}{{{y}^{4}}}}{{{{x}^{4}}}{{{y}^{3}}}}$.
Vemos que tenemos las variables x y y, por lo tanto, aplicamos la regla del cociente a cada variable separadamente:
$latex \frac{x^3y^4}{x^4y^3}=(x^{3-4})(y^{4-3})$
$latex ={{{x}^{-1}}}{{{y}^{1}}}$
$latex =\frac{y}{x}$
5) Potencia de una potencia de exponentes
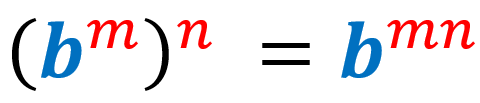
Cuando una expresión exponencial es elevada a una potencia, copiamos la base y multiplicamos los exponentes. Nuevamente, asumimos que la base es diferente de cero y los exponentes son números enteros.
EJEMPLOS
- Simplifica la expresión exponencial $latex {{\left( {{{x}^{2}}} \right)}^{3}}$.
Esta expresión tiene un exponente interior y otro exterior. La regla de la potencia de una potencia nos dice que copiemos la base y multipliquemos los exponentes:
$latex {{\left( {{{x}^{2}}} \right)}^{3}}= {{{x}^{(2)(3)}}}$
$latex ={{{x}^{6}}}$
- Simplifica la expresión exponencial $latex {{\left( {{{x}^{3}}}{{{y}^{5}}} \right)}^{4}}$.
Aplicamos la regla de la potencia de una potencia separadamente:
$latex {{\left( {{{x}^{3}}}{{{y}^{5}}} \right)}^{4}}={{{x}^{(3)(4)}}}{{{y}^{(4)(5)}}}$
$latex ={{{x}^{12}}}{{{y}^{20}}}$
6) Potencia de un producto de exponentes
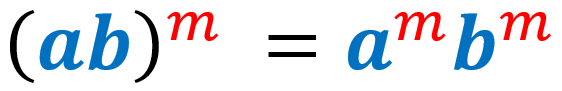
Cuando tenemos el producto de dos o más factores elevados a una potencia, copiamos cada factor y luego multiplicamos el exponente exterior por su exponente. Tenemos que realizar esto para cada factor dentro del paréntesis. Aquí asumimos que las bases son diferentes de cero y los exponentes son números enteros.
EJEMPLOS
- Simplifica la expresión exponencial $latex {{\left( {{{3}^{2}}{{x}^{3}}{{y}^{4}}} \right)}^{3}}$.
Aquí tenemos tres factores, cada uno con exponentes. Simplemente, tenemos que copiar cada factor y multiplicar su exponente por el exponente exterior:
$latex {{\left( {{{3}^{2}}{{x}^{3}}{{y}^{4}}} \right)}^{3}}=({{{3}^{(2)(3)}}{{x}^{(3)(3)}}{{y}^{(4)(3)}}})$
$latex ={{{3}^{6}}{{x}^{9}}{{y}^{12}}}$
7) Potencia de un cociente de exponentes
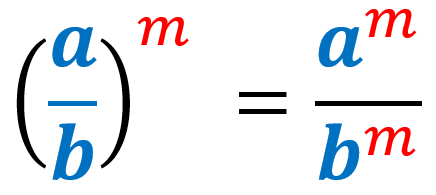
Cuando un cociente está elevado a una potencia, copiamos el factor en el numerador y multiplicamos su exponente por el exponente exterior. Luego, realizamos lo mismo con el factor en el denominador. Asumimos que las bases son diferentes de cero y que los exponentes son números enteros.
EJEMPLOS
- Simplifica la expresión exponencial $latex {{\left( {\frac{{{{x}^{3}}}}{{{{y}^{5}}}}} \right)}^{4}}$.
Usando la regla de potencia de un cociente de exponentes. Copiamos las bases en el numerador y el denominador y multiplicamos sus exponentes por el exponente exterior:
$latex {{\left( {\frac{{{{x}^{3}}}}{{{{y}^{5}}}}} \right)}^{4}}={\frac{{{{x}^{(3)(4)}}}}{{{{y}^{(5)(4)}}}}}$
$latex ={\frac{{{{x}^{12}}}}{{{{y}^{20}}}}}$
Véase también
¿Interesado en aprender más sobre otros temas algebraicos? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
