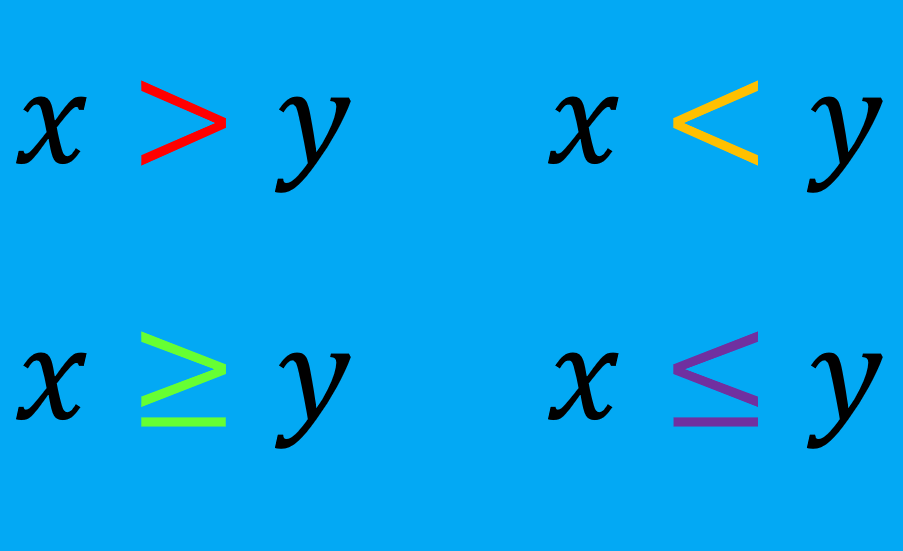Las desigualdades con valor absoluto siguen las mismas reglas que el valor absoluto en números; la diferencia es que en las desigualdades tenemos una variable. En este artículo, miraremos una introducción breve a las desigualdades con valor absoluto y aprenderemos un método para resolver desigualdades con valor absoluto.
Finalmente, miraremos unos ejemplos resueltos para mejorar el entendimiento de los conceptos.
¿Qué son las desigualdades con valor absoluto?
Antes de empezar con las desigualdades con valor absoluto, recordemos lo que es el valor absoluto de un número.
Empecemos con la definición: el valor absoluto de un número es la distancia de un valor desde el origen sin importar la dirección. El valor absoluto está denotado por dos líneas verticales que encierran al número o expresión.
Por ejemplo, el valor absoluto de $latex x$ es expresado como $latex \left| x \right|=a$, lo cual significa que $latex x=+a$ y $latex x=-a$. Ahora veamos lo que significan las desigualdades con valor absoluto.
Una desigualdad con valor absoluto es una expresión con la función valor absoluto, así como también con los signos de valor absoluto. Por ejemplo, la expresión $latex \left| x +5\right|>2$ es una desigualdad con valor absoluto que contiene un signo “mayor que”.
Tenemos cuatro símbolos de desigualdades diferentes: mayor que (>), menor que(<), mayor o igual que (≥) y menor o igual que (≤).
EJEMPLOS
Las siguientes son desigualdades con valor absoluto:
- $latex \left| x+1\right|<3$
- $latex \left| x-2\right|≥5$
- $latex \left| x+5\right|>1$
¿Cómo resolver desigualdades con valor absoluto?
Los pasos para resolver desigualdades con valor absoluto son similares a los pasos para resolver ecuaciones, con la diferencia que tenemos que tener en cuenta un poco de información extra para resolver las desigualdades.
Los siguientes pasos son reglas generales que pueden seguirse para resolver desigualdades con valor absoluto:
Paso 1: Despejar completamente la expresión con el valor absoluto.
Paso 2: Resolver las versiones positivas y negativas de las desigualdades con valor absoluto.
- Cuando el número en el otro lado del signo de desigualdad es negativo, concluimos que, o bien todos los números reales son soluciones o que la desigualdad no tiene solución.
- Cuando el número en el otro lado es positivo, procedemos a formar una desigualdad compuesta al remover las barras del valor absoluto.
Paso 3: El tipo de signo de desigualdad determina el formato de la desigualdad compuesta a ser formada.
- Si es que un problema contiene signos mayor que o mayor/igual que, forma una desigualdad compuesta de la siguiente manera:
(valores dentro del signo de valor absoluto)< -(el número en el otro lado)
o
(valores dentro del signo de valor absoluto)> (el número en el otro lado)
- De igual forma, si es que un problema contiene signos menor que o menor/igual que, forma una desigualdad compuesta de tres partes de la siguiente manera:
-(el número en el otro lado del signo)<(valores dentro del signo de valor absoluto)< (el número en el otro lado del signo)
Paso 4: Resuelve las desigualdades.
Ejemplos resueltos
EJEMPLO 1
Resuelve la desigualdad $latex |x+4|-6<9$.
Paso 1: Despeja el valor absoluto:
$latex |x+4|-6<9$
$latex |x+4|<9+6$
$latex |x+4|<15$
Paso 2: ¿Es el número en el otro lado negativo? No, es un número positivo, 15. Nos movemos al paso 3.
Paso 3: Forma una desigualdad compuesta: El signo de desigualdad en este problema es un signo menor que, por lo que formamos una desigualdad de tres partes:
$latex -15<x+4<15$
Paso 4: Resuelve la desigualdad:
$latex -15-4<x<15-4$
$latex -19<x<11$
EJEMPLO 2
Resuelve la desigualdad $latex |2x-1|-7≥-3$.
Paso 1: Despeja el valor absoluto:
$latex |2x-1|-7≥-3$
$latex |2x-1|≥-3+7$
$latex |2x-1|≥4$
Paso 2: ¿Es el número en el otro lado negativo? No, es un número positivo, 4. Nos movemos al paso 3.
Paso 3: Forma una desigualdad compuesta: El signo de desigualdad en este problema es un signo mayor/igual que, por lo que formamos una desigualdad compuesta con la palabra “o”:
$latex 2x-1≤-4$ o $latex 2x-1≥4$
Paso 4: Resuelve las desigualdades:
$latex 2x-1≤-4$ o $latex 2x-1≥4$
$latex 2x≤-3$ o $latex 2x≥5$
$latex x\le -\frac{3}{2}$ o $latex x\ge \frac{5}{2}$
EJEMPLO 3
Resuelve la desigualdad $latex |5x+6|+4<1$.
Paso 1: Despeja el valor absoluto:
$latex |5x+6|+4<1$
$latex |5x+6|<1-4$
$latex |5x+6|<-3$
Paso 2: ¿Es el número en el otro lado negativo? Sí, es un número negativo, -3. Miraremos a los signos de cada lado de la desigualdad para determinar la solución al problema:
$latex |5x+6|<-3$
positivo $latex <$ negativo
Este enunciado nunca es verdadero, por lo que el problema no tiene solución.
EJEMPLO 4
Resuelve la desigualdad $latex |3x-4|+9>5$.
Paso 1: Despeja el valor absoluto:
$latex |3x-4|+9>5$
$latex |3x-4|>5-9$
$latex |3x-4|>-4$
Paso 2: ¿Es el número en el otro lado negativo? Sí, es un número negativo, -4. Vamos a mirar los signos de cada lado de la desigualdad para determinar la solución para el problema:
$latex |3x-4|>-4$
positivo $latex >$ negativo
Este enunciado siempre es verdadero, por lo que la solución al problema es todos los números reales.
Inténtalo tú mismo – Resuelve los ejercicios
Véase también
¿Interesado en aprender más sobre ecuaciones? Mira estas páginas: