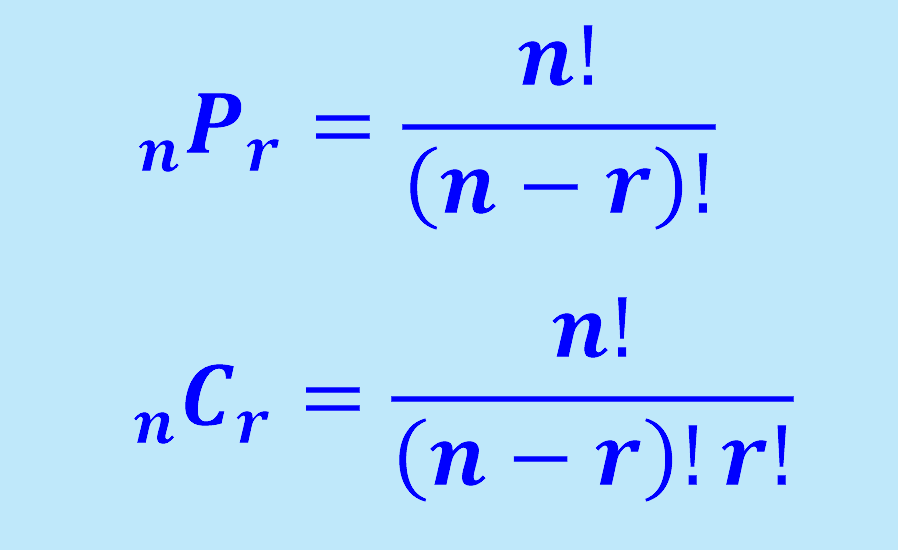Las permutaciones y las combinaciones son maneras de representar grupos de objetos al seleccionarlos de un conjunto y formar subconjuntos. Con las permutaciones y las combinaciones podemos organizar ciertos grupos de datos.
Miraremos una introducción a las permutaciones y las combinaciones y aprenderemos a usar sus fórmulas.
ÁLGEBRA
Relevante para…
Conocer las fórmulas de las permutaciones y las combinaciones y resolver ejercicios.
ÁLGEBRA
Relevante para…
Conocer las fórmulas de las permutaciones y las combinaciones y resolver ejercicios.
¿Qué es una permutación?
Las permutaciones se refieren a la acción de organizar a todos los miembros de un conjunto en algún tipo de orden o secuencia. Esto significa que si es que un conjunto ya está ordenado, el proceso de reorganizar sus elementos se llama permutar.
Con las permutaciones, el orden de los elementos sí importa. Si es que nuestra contraseña es 1234 e ingresamos los números 3241, la contraseña será incorrecta, ya que tenemos los mismos números, pero en un orden diferente. Esto significa que 3421 es una permutación de 1234.
EJEMPLO
Las permutaciones de 1, 2, 3, 4 son:
- 4321, 4312, 4123, 4132, 4213, 4231, 3412, 3421, 3214, 3241, 3124, 3142, 2413, 2431, 2314, 2341, 2134, 2143, 1432, 1423, 1324, 1342, 1234, 1243.
¿Qué es una combinación?
Una permutación se relaciona a la acción de organizar los elementos de una colección de modo que, a diferencia de las permutaciones, el orden de la selección no importa. Por ejemplo, escoger un equipo de 3 personas de un grupo de 20 personas es una combinación.
EJEMPLO
Si es que tenemos los números 1, 2, 3, 4, 5 y tenemos que escoger 3 números, podemos obtener los siguientes conjuntos:
- 123, 234, 345, 124, 125, 134, 145, 135, 235, 245.
Estos son los únicos conjuntos posibles, ya que al escoger 123, obtendremos los mismos números que 132, 213, 231, 321, 312.
Permutaciones y combinaciones fórmulas
Las fórmulas de las permutaciones y las combinaciones pueden tener diferentes variaciones, pero las tres más importantes son:
Fórmula de las permutaciones
Si es que tenemos una colección de n objetos, entonces el número de maneras que podemos escoger r de ellos es igual a:
$$_{n}P_{r}=\frac{n!}{(n-r)!}$$
Fórmulas de las combinaciones
Si es que no quisieramos tomar en cuenta las diferentes permutaciones de los elementos, podemos dividir la expresión de arriba por el número de permutaciones de r, el cual es r!. Este resultado es llamado combinaciones:
$$_{n}C_{r}=\frac{_{n}P_{r}}{r!}$$
Al reescribir esta fórmula, podemos obtener la fórmula de las combinaciones general:
$$_{n}C_{r}=\frac{n!}{(n-r)!r!}$$
Aplicar las fórmulas de permutaciones y combinaciones
EJEMPLO 1
Encuentra el número de combinaciones si es que $latex n=10$ y $latex r=3$.
Solución: Simplemente, podemos usar la fórmula de las combinaciones reemplazando los valores $latex n=10$ y $latex r=3$:
$latex _{n}{{C}_{r}}=\frac{{n!}}{{\left( {n-r} \right)!r!}}$
$latex =\frac{{10!}}{{\left( {10-3} \right)!3!}}$
$latex =\frac{{10!}}{{\left( {7} \right)!3!}}$
$latex =\frac{{10\times 9\times 8\times 7!}}{{\left( 7 \right)!3!}}=120$
EJEMPLO 2
Encuentra el número de permutaciones si es que $latex n=10$ y $latex r=3$.
Solución: Nuevamente, sólo tenemos que usar la fórmula de las permutaciones y reemplazar los valores $latex n=10$ y $latex r=3$:
$latex _{n}{{P}_{r}}=\frac{{n!}}{{\left( {n-r} \right)!}}$
$latex =\frac{{10!}}{{\left( {10-3} \right)!}}$
$latex =\frac{{10!}}{{\left( {7} \right)!}}$
$latex =\frac{{10\times 9\times 8\times 7!}}{{\left( 7 \right)!}}=720$
EJEMPLO 3
¿Cuántas formas existen de escoger un grupo de 5 personas de un grupo de 12 personas?
Solución: Este es un problema de combinaciones, entonces usamos la fórmula de las combinaciones con los valores $latex n=12$ y $latex r=4$:
$latex _{n}{{C}_{r}}=\frac{{n!}}{{\left( {n-r} \right)!r!}}$
$latex =\frac{{12!}}{{\left( {12-4} \right)!4!}}$
$latex =\frac{{12!}}{{\left( {8} \right)!4!}}$
$latex =\frac{{12\times 11\times 10\times 9\times 8!}}{{\left( 8 \right)!4!}}=495$
EJEMPLO 4
¿Cuántas formas existen de formar una lista de 4 postres de un menú de 10 postres?
Solución: Nuevamente, solo tenemos que usar la fórmula de las permutaciones y reemplazar los valores $latex n=10$ y $latex r=4$:
$latex _{n}{{P}_{r}}=\frac{{n!}}{{\left( {n-r} \right)!}}$
$latex =\frac{{10!}}{{\left( {10-4} \right)!}}$
$latex =\frac{{10!}}{{\left( {6} \right)!}}$
$latex =\frac{{10\times 9\times 8\times 7\times 6!}}{{\left( 6 \right)!}}=5040$
Inténtalo tú mismo – Resuelve los siguientes ejercicios
Preguntas frecuentes
¿Cuál es la diferencia principal entre combinaciones y permutaciones?
Una permutación es un acto de organizar elementos en orden. Las combinaciones son maneras de seleccionar objetos de un grupo de una forma en la que el orden de los objetos no importa.
¿Cuáles son las fórmulas para las combinaciones y las permutaciones?
La fórmula para las permutaciones es $latex _{n}{{P}_{r}}=\frac{{n!}}{{\left( {n-r} \right)!}}$.
La fórmula para las combinaciones es $latex _{n}{{C}_{r}}=\frac{{n!}}{{\left( {n-r} \right)!r!}}$.
¿Cuál es la relación entre las permutaciones y las combinaciones?
Las permutaciones y las combinaciones pueden ser relacionadas con la fórmula $latex _{n}{{C}_{r}}=\frac{{_{n}{{P}_{r}}n!}}{{r!}}$.
¿Cuáles son ejemplos de permutaciones y las combinaciones?
Organizar dígitos, letras, personas son ejemplos de permutaciones.
Seleccionar objetos de un menú, seleccionar personas de un grupo son ejemplos de combinaciones.
Véase también
¿Interesado en aprender más sobre otros temas algebraicos? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
