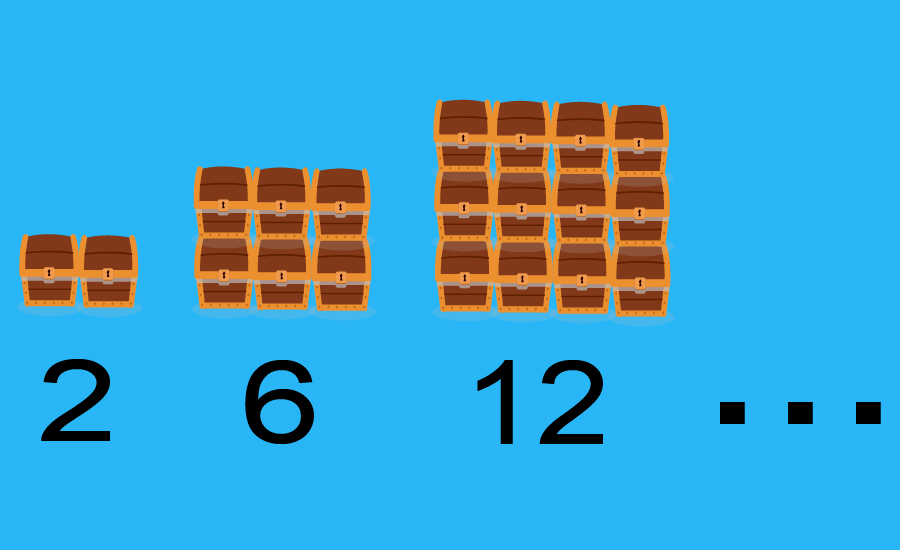Las dos sucesiones más simples con las que podemos trabajar son las sucesiones aritméticas y geométricas. Las sucesiones aritméticas se caracterizan porque sus términos son formados al sumar una diferencia común. Por otro lado, las sucesiones geométricas son formadas al multiplicar a los términos por una razón común.
En este artículo, exploraremos estas sucesiones y aprenderemos a escribir términos tanto de sucesiones aritméticas como de sucesiones geométricas. También aprenderemos a resolver algunos ejercicios.
Sucesiones aritméticas
Una sucesión aritmética es una lista de números con un patrón definido. Si es que tomamos un número de la sucesión y luego lo restamos por el número previo y el resultado siempre es el mismo, entonces es una sucesión aritmética.
La diferencia constante en todos los pares de números consecutivos en una sucesión es llamada la diferencia común, denotada por la letra d. Usamos la diferencia común para ir de un término al otro. Si es que tomamos un término en la sucesión y sumamos la diferencia común, nos moveremos al siguiente término. Así es como los términos en una sucesión aritmética son generados.
Si es que la diferencia común entre los términos es positiva, decimos que la sucesión está incrementando. Por otro lado, cuando la diferencia entre los términos es negativa, decimos que la sucesión está decreciendo.
Los siguientes son dos ejemplos de sucesiones aritméticas. Observa sus diferencias comunes.
Fórmula de la sucesión aritmética
Si es que queremos encontrar cualquier término (conocido como el término n) en la sucesión aritmética, podemos usar la fórmula de la sucesión aritmética para lograr esto. Lo único que tenemos que hacer es extraer o identificar valores del problema que serán sustituidos en la fórmula.
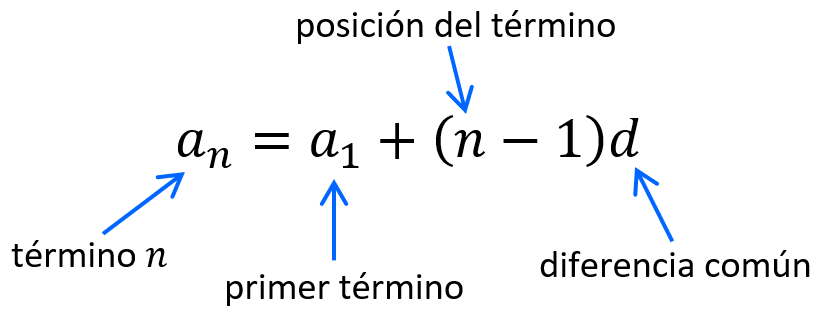
Veamos las partes esenciales de la fórmula:
en donde tenemos:
- $latex {{a}_{n}}=$ término que queremos encontrar
- $latex {{a}_{1}}=$ primer término en la lista ordenada de números
- $latex n=$ la posición del término, por ejemplo, 5 para el quinto término
- $latex d=$ la diferencia común de cualquier par de términos consecutivos
Ejemplos de sucesiones aritméticas
EJEMPLO 1
Encuentra el siguiente término en la siguiente sucesión:
4, 7, 10, 13, 16, ?
Solución
Primero, encontramos la diferencia común en cada par de números consecutivos:
- $latex 7-4=3$
- $latex 10-7=3$
- $latex 13-10=3$
- $latex 16-13=3$
Dado que $latex d=3$, podemos encontrar el término que sigue después del 16 simplemente sumando 3. Entonces, tenemos $latex 16+3=19$.
4, 7, 10, 13, 16, 19
EJEMPLO 2
Encuentra el siguiente término en la siguiente sucesión:
29, 22, 15, 8, ?
Solución
Primero, encontramos la diferencia común en cada par de números consecutivos:
- $latex 22-29=-7$
- $latex 15-22=-7$
- $latex 8-15=-7$
Dado que $latex d=-7$, podemos encontrar el término que sigue después del 8 simplemente sumando -7. Entonces, tenemos $latex 8+(-7)=1$.
29, 22, 15, 8, 1
EJEMPLO 3
Encuentra el término 20 en la siguiente sucesión aritmética:
3, 6, 9, 12, …
Solución
Necesitamos tres cosas para encontrar el término 20 usando la fórmula:
- El primer término $latex ({{a}_{1}})$
- La diferencia común entre términos consecutivos $latex (d)$
- La posición del término $latex (n)$
Entonces tenemos:
- primer término$latex ={{a}_{1}}=3$
- diferencia común $latex =d=3$
- posición del término $latex =n=20$
y sustituimos los valores en la fórmula:
$latex {{a}_{n}}={{a}_{1}}+(n-1)d$
$latex {{a}_{20}}=3+(20-1)3$
$latex {{a}_{20}}=3+(19)3$
$latex {{a}_{20}}=3+57$
$latex {{a}_{20}}=60$
EJEMPLO 4
Encuentra el término 15 en la siguiente sucesión aritmética:
25, 21, 17, 13, …
Solución
Solución: Necesitamos tres cosas para encontrar el término 15 usando la fórmula:
- El primer término $latex ({{a}_{1}})$
- La diferencia común entre términos consecutivos $latex (d)$
- La posición del término $latex (n)$
Entonces tenemos:
- primer término$latex ={{a}_{1}}=25$
- diferencia común $latex =d=-4$
- posición del término $latex =n=15$
y sustituimos los valores en la fórmula:
$latex {{a}_{n}}={{a}_{1}}+(n-1)d$
$latex {{a}_{15}}=25+(15-1)(-4)$
$latex {{a}_{15}}=25+(14)(-4)$
$latex {{a}_{15}}=25-56$
$latex {{a}_{15}}=-31$
EJEMPLO 5
Encuentra el término 22 en la siguiente sucesión aritmética:
5, 11, 17, 23, …
Solución
Necesitamos tres cosas para encontrar el término 22 usando la fórmula:
- El primer término $latex ({{a}_{1}})$
- La diferencia común entre términos consecutivos $latex (d)$
- La posición del término $latex (n)$
Entonces tenemos:
- primer término$latex ={{a}_{1}}=5$
- diferencia común $latex =d=6$
- posición del término $latex =n=22$
y sustituimos los valores en la fórmula:
$latex {{a}_{n}}={{a}_{1}}+(n-1)d$
$latex {{a}_{22}}=5+(22-1)6$
$latex {{a}_{22}}=5+(21)6$
$latex {{a}_{22}}=5+126$
$latex {{a}_{22}}=131$
Inténtalo tú mismo – Resuelve los ejercicios
Sucesiones geométricas
Una sucesión geométrica es una sucesión de números que sigue un patrón en donde el siguiente término es encontrado al multiplicar por una constante llamada la razón común r.
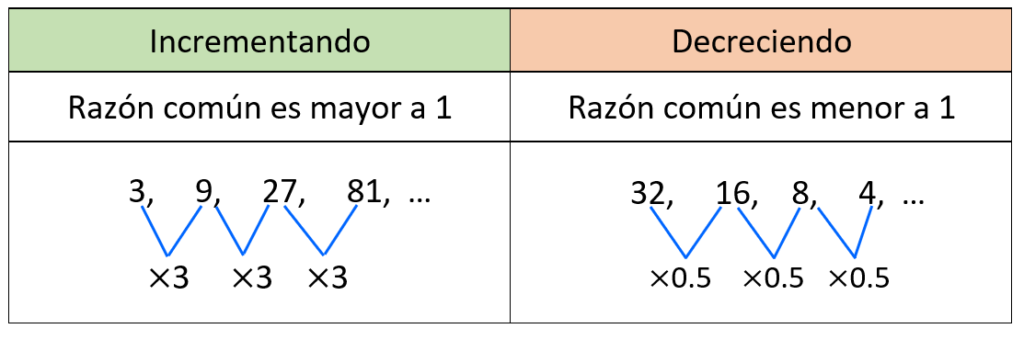
Similar a las sucesiones aritméticas, las sucesiones geométricas también pueden incrementar o decrecer. Sin embargo, en las sucesiones geométricas, esto depende en si la razón común es mayor a 1 o menor a 1:
Fórmula de la sucesión geométrica
Si es que queremos encontrar cualquier término (conocido como el término n) en la sucesión geométrica, podemos usar la fórmula de la sucesión geométrica para lograr esto. Sólo necesitamos extraer la información necesaria del problema para reemplazarla en la fórmula.
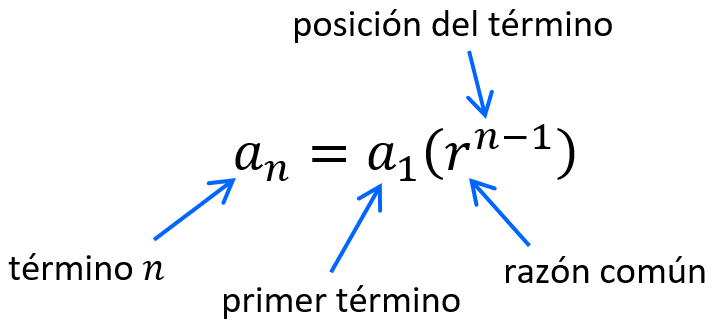
Las siguientes son las partes esenciales de la fórmula:
en donde tenemos:
- $latex {{a}_{n}}=$ término que queremos encontrar
- $latex {{a}_{1}}=$ primer término en la sucesión
- $latex n=$ la posición del término, por ejemplo, 4 para el cuarto término
- $latex r=$ la razón común
La razón común puede ser calculada al dividir un término por el término previo:
$$r=\frac{{{{a}_{n}}}}{{{{a}_{{n-1}}}}}$$
Ejemplos de sucesiones geométricas
EJEMPLO 1
Encuentra el siguiente término en la siguiente sucesión:
5, 15, 45, 135, ?
Solución
Primero, encontramos la razón común en cada par de números consecutivos:
- $latex r=\frac{15}{5}=3$
- $latex r=\frac{45}{15}=3$
- $latex r=\frac{135}{45}=3$
Dado que $latex r=3$, podemos encontrar el término que sigue después del 135 simplemente multiplicando por 3. Entonces, tenemos $latex 135(3)=405$.
5, 15, 45, 135, 405
EJEMPLO 2
Encuentra el siguiente término en la siguiente sucesión:
4, -20, 100, -500, 2500, ?
Solución
Primero, encontramos la razón común en cada par de números consecutivos:
- $latex r=\frac{-20}{4}=-5$
- $latex r=\frac{100}{-20}=-5$
- $latex r=\frac{-500}{100}=-5$
- $latex r=\frac{2500}{-500}=-5$
Dado que $latex r=-5$, podemos encontrar el término que sigue después del 2500 simplemente multiplicando por -5. Entonces, tenemos $latex 2500(-5)=-12500$.
4, -20, 100, -500, 2500, -12500
EJEMPLO 3
Encuentra el siguiente término en la siguiente sucesión:
-80, 40, -20, 10, ?
Solución
Primero, encontramos la razón común en cada par de números consecutivos:
- $latex r=\frac{40}{-80}=-0.5$
- $latex r=\frac{-20}{40}=-0.5$
- $latex r=\frac{10}{-20}=-0.5$
Dado que $latex r=-0.5$, podemos encontrar el término que sigue después del 10 simplemente multiplicando por -0.5. Entonces, tenemos $latex 10(-0.5)=-5$.
-80, 40, -20, 10, -5
EJEMPLO 4
Encuentra el término 10 en la siguiente sucesión geométrica:
2, 4, 8, 16, …
Solución
Necesitamos tres cosas para encontrar el término 10 usando la fórmula:
- El primer término $latex ({{a}_{1}})$
- La razón común entre términos consecutivos $latex (r)$
- La posición del término $latex (n)$
Entonces tenemos:
- primer término$latex ={{a}_{1}}=2$
- razón común $latex =r=\frac{4}{2}=2$
- posición del término $latex =n=10$
y sustituimos los valores en la fórmula:
$latex {{a}_{n}}={{a}_{1}}\left( {{{r}^{{n-1}}}} \right)$
$latex {{a}_{10}}=2\left( {{{2}^{{10-1}}}} \right)$
$latex {{a}_{10}}=2\left( {{{2}^{{9}}}} \right)$
$latex {{a}_{10}}=2(512)$
$latex {{a}_{10}}=1024$
EJEMPLO 5
Encuentra el término 6 en la siguiente sucesión geométrica:
3, 12, 48, 192, …
Solución
Necesitamos tres cosas para encontrar el término 6 usando la fórmula:
- El primer término $latex ({{a}_{1}})$
- La razón común entre términos consecutivos $latex (r)$
- La posición del término $latex (n)$
Entonces tenemos:
- primer término$latex ={{a}_{1}}=3$
- razón común $latex =r=\frac{12}{3}=4$
- posición del término $latex =n=6$
y sustituimos los valores en la fórmula:
$latex {{a}_{n}}={{a}_{1}}\left( {{{r}^{{n-1}}}} \right)$
$latex {{a}_{6}}=3\left( {{{4}^{{6-1}}}} \right)$
$latex {{a}_{6}}=3\left( {{{4}^{{5}}}} \right)$
$latex {{a}_{6}}=3(1024)$
$latex {{a}_{6}}=3072$
EJEMPLO 6
Encuentra el término 6 en la siguiente sucesión geométrica:
-2400, 1200, -600, 300, …
Solución
Necesitamos tres cosas para encontrar el término 6 usando la fórmula:
- El primer término $latex ({{a}_{1}})$
- La razón común entre términos consecutivos $latex (r)$
- La posición del término $latex (n)$
Entonces tenemos:
- primer término$latex ={{a}_{1}}=-2400$
- razón común $latex =r=\frac{1200}{-2400}=-0.5$
- posición del término $latex =n=6$
y sustituimos los valores en la fórmula:
$latex {{a}_{n}}={{a}_{1}}\left( {{{r}^{{n-1}}}} \right)$
$latex {{a}_{6}}=-2400\left( {{{-0.5}^{{6-1}}}} \right)$
$latex {{a}_{6}}=-2400\left( {{{-0.5}^{{5}}}} \right)$
$latex {{a}_{6}}=-2400(-0.03125)$
$latex {{a}_{6}}=75$
Inténtalo tú mismo – Resuelve los ejercicios
Véase también
¿Interesado en aprender más sobre otros temas algebraicos? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
