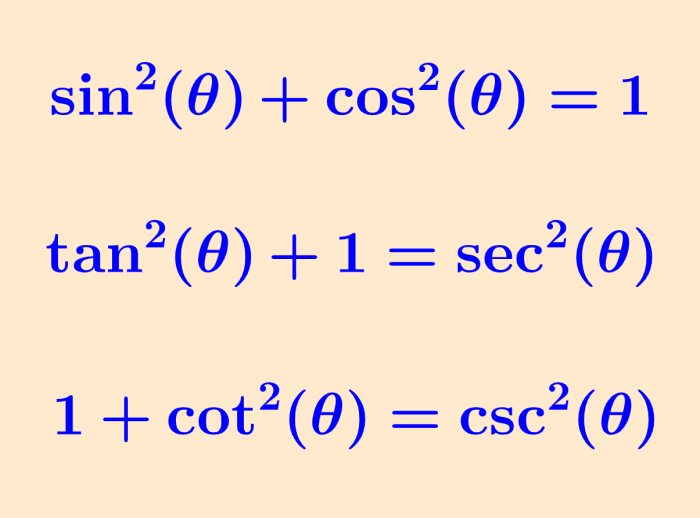Las identidades Pitagóricas son identidades en trigonometría que son extensiones del teorema de Pitágoras. Las identidades Pitagóricas son útiles para simplificar expresiones trigonométricas. Estas identidades son especialmente usadas para escribir expresiones como una función de seno o coseno, como las fórmulas del ángulo doble.
A continuación, conoceremos las identidades Pitagóricas y aprenderemos a derivarlas a partir del teorema de Pitágoras. Luego, veremos algunos ejercicios de práctica en donde aplicaremos estas identidades.
TRIGONOMETRÍA
Relevante para…
Aprender sobre las identidades pitagóricas con ejercicios.
TRIGONOMETRÍA
Relevante para…
Aprender sobre las identidades pitagóricas con ejercicios.
¿Cuáles son las identidades Pitagóricas?
Las identidades Pitagóricas son ecuaciones que contienen funciones trigonométricas, las cuales son verdaderas para todos los valores sustituidos en las variables. Las identidades trigonométricas son especialmente útiles para simplificar expresiones trigonométricas. Las identidades trigonométricas son derivadas del teorema de Pitágoras:
| $latex {{\sin}^2} (\theta)+{{\cos}^2} (\theta)=1$ |
Esta es la identidad Pitagórica más importante. Esta identidad es verdadera para todos los valores de θ. Usando esta primera identidad, podemos crear dos identidades Pitagóricas adicionales:
| $latex {{\tan}^2} (\theta)+1={{\sec}^2} (\theta)$ $latex 1+{{\cot}^2} (\theta)={{\csc}^2} (\theta)$ |
en donde, «tan» representa a la función tangente, «sec» representa a la función secante, «cot» representa a la función cotangente y «csc» representa a la función cosecante.
¿Cómo derivar las identidades Pitagóricas?
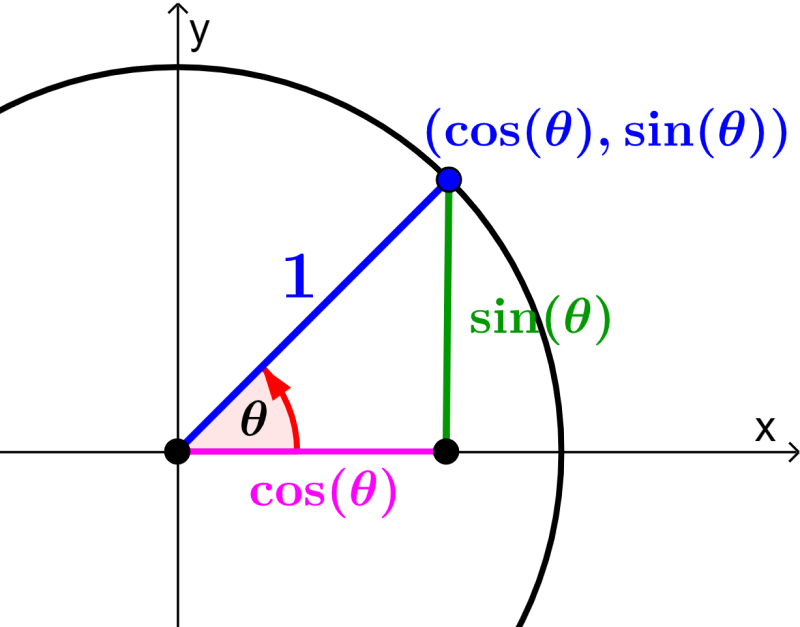
Podemos derivar las identidades Pitagóricas usando al círculo unitario. Recordemos que el círculo unitario es un círculo con un radio de 1. En este triángulo, las coordenadas en x son representadas por $latex \cos(\theta)$ y las coordenadas en y son representadas por $latex \sin(\theta)$ como se muestra en el siguiente diagrama:
Vemos que los catetos del triángulo rectángulo en el círculo unitario tienen los valores de $latex \sin(\theta)$ y $latex \cos(\theta)$. Además, la hipotenusa del triángulo es el radio del círculo, el cual es igual a 1. Entonces, usando el teorema de Pitágoras, tenemos:
$latex {{\sin}^2}(\theta)+{{\cos}^2}(\theta)=1$
Esta es la identidad Pitagórica principal. Usando esta identidad, podemos derivar dos identidades adicionales.
Empezamos con la primera identidad Pitagórica:
$latex {{\sin}^2}(\theta)+{{\cos}^2}(\theta)=1$
Dividimos a cada término por $latex {{\cos}^2}(\theta)$:
$$\frac{{{\sin}^2}(\theta)}{{{\cos}^2}(\theta)}+\frac{{{\cos}^2}(\theta)}{{{\cos}^2}(\theta)}=\frac{1}{{{\cos}^2}(\theta)}$$
Ahora, sabemos que tenemos $latex \frac{\sin(\theta)}{\cos(\theta)}=\tan(\theta)$ y $latex \frac{1}{\cos(\theta)}=\sec(\theta)$. Entonces, al sustituir y simplificar, tenemos:
$latex {{\tan}^2}(\theta)+1={{\sec}^2}(\theta)$
Si es que dividimos por un valor diferente, podemos encontrar la tercera identidad Pitagórica. Empezamos con la primera identidad Pitagórica:
$latex {{\sin}^2}(\theta)+{{\cos}^2}(\theta)=1$
Dividimos a cada término por $latex {{\sin}^2}(\theta)$:
$$\frac{{{\sin}^2}(\theta)}{{{\sin}^2}(\theta)}+\frac{{{\cos}^2}(\theta)}{{{\sin}^2}(\theta)}=\frac{1}{{{\sin}^2}(\theta)}$$
Ahora, podemos usar las relaciones $latex \frac{\cos(\theta)}{\sin(\theta)}=\cot(\theta)$ y $latex \frac{1}{\sin(\theta)}=\csc(\theta)$. Entonces, al sustituir y simplificar, tenemos:
$latex 1+{{\cot}^2}(\theta)={{\csc}^2}(\theta)$
Ejercicios de identidades Pitagóricas resueltos
Las identidades Pitagóricas derivadas arriba son usadas para resolver los siguientes ejercicios. Intenta resolver los ejercicios tú mismo antes de mirar la respuesta.
EJERCICIO 1
Simplifica la expresión $latex \sin(x){{\cos}^2}(x)-\sin(x)$ usando las identidades Pitagóricas.
Solución
Esta expresión contiene al seno y al coseno, por lo que podemos usar la identidad $latex {{\sin}^2}(x)+{{\cos}^2}(x)=1$. Entonces, empezamos factorizando a la expresión dada:
$$\sin(x){{\cos}^2}(x)-\sin(x)=\sin(x)({{\cos}^2}(x)-1)$$
Podemos reescribir a la identidad $latex {{\sin}^2}(x)+{{\cos}^2}(x)=1$ de la siguiente forma: $latex {{\cos}^2}(x)-1=-{{\sin}^2}(x)$. Entonces, al reemplazar a esta identidad, tenemos:
$$\sin(x)({{\cos}^2}(x)-1)=\sin(x)(-{{\sin}^2}(x))$$
$latex ={{\sin}^3}(x)$
EJERCICIO 2
Expresa a la expresión trigonométrica $latex {{\csc}^2}(x)-\cot(x)-3$ en forma factorizada.
Solución
Podemos usar la identidad Pitagórica $latex 1+{{\cot}^2}(x)={{\csc}^2}(x)$. Entonces, sustituyendo, tenemos:
$latex {{\csc}^2}(x)-\cot(x)-3$
$latex =1+\cot^2(x)-\cot(x)-3$
$latex =\cot^2(x)-\cot(x)-2$
$latex =(\cot(x)-2)(\cot(x)+1)$
EJERCICIO 3
Simplifica la expresión trigonométrica $$({{\sec}^2}(x))(1-{{\sin}^2}(x))-(\frac{\sin(x)}{\csc(x)}+\frac{\cos(x)}{\sec(x)})$$
Solución
En este caso, tenemos que reconocer que $latex \sec(x)=\frac{1}{\cos(x)}$ y $latex \csc(x)=\frac{1}{\sin(x)}$. Usando esto, tenemos:
$$({{\sec}^2}(x))(1-{{\sin}^2}(x))-(\frac{\sin(x)}{\csc(x)}+\frac{\cos(x)}{\sec(x)})$$
$$=({{\sec}^2}(x))(1-{{\sin}^2}(x))-({{\sin}^2}(x)+{{\cos}^2}(x))$$
Ahora, usamos la identidad Pitagórica principal y tenemos:
$latex =({{\sec}^2}(x))({{\cos}^2}(x))-(1)$
$latex =1-1$
$latex =0$
EJERCICIO 4
Si es que tenemos que $latex \tan(\theta)=\frac{1}{3}$, ¿cuál es el valor de $latex \frac{1}{{{\sin}^2}(\theta)}+\frac{1}{{{\cos}^2}(\theta)}$?
Solución
Podemos usar la segunda y la tercera identidades Pitagóricas. Además, recordamos que la secante es igual a $latex \frac{1}{\cos(\theta)}$ y la cosecante es igual a $latex \frac{1}{\sin(\theta)}$. Usando esto, tenemos:
$latex {{\tan}^2}(\theta)+1={{\sec}^2}(\theta)=\frac{1}{{{\cos}^2}(\theta)}$
$latex {{\cot}^2}(\theta)+1={{\csc}^2}(\theta)=\frac{1}{{{\sin}^2}(\theta)}$
Sustituyendo esto en la expresión original, tenemos:
$latex \frac{1}{{{\sin}^2}(\theta)}+\frac{1}{{{\cos}^2}(\theta)}$
$latex ={{\cot}^2}(\theta)+1+{{\tan}^2}(\theta)+1$
Ahora, sabemos que $latex \tan(\theta)=\frac{1}{3}$. Además, dado que la cotangente es la función recíproca de la tangente, esto significa que $latex \cot(\theta)=3$. Usando estos valores, tenemos:
$latex {{\cot}^2}(\theta)+1+{{\tan}^2}(\theta)+1$
$latex ={{3}^2}+1+(\frac{1}{3})^2+1$
$latex =\frac{100}{9}$
Véase también
¿Interesado en aprender más sobre identidades trigonométricas? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
