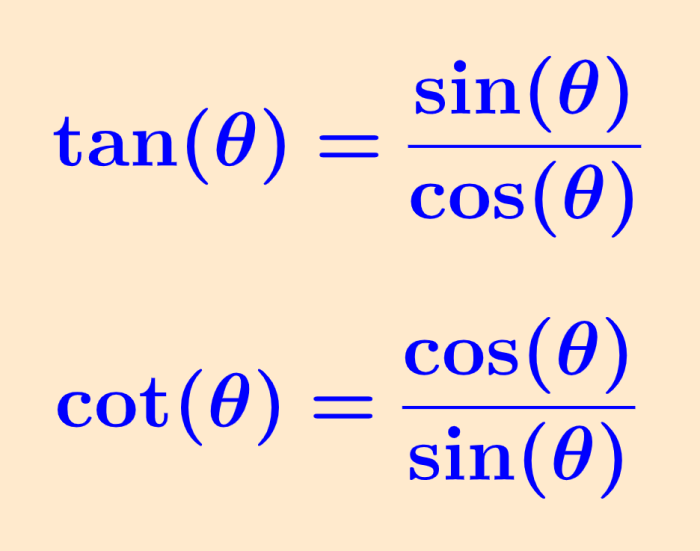Las identidades de cociente son identidades trigonométricas que son escritas como fracciones de las funciones seno y coseno. La tangente forma una identidad de cociente y pude ser escrita como el seno del ángulo dividido por el coseno. De igual forma, la cotangente puede ser escrita como el coseno del ángulo dividido por el seno.
A continuación, conoceremos el origen de las identidades de cociente. Luego, usaremos estas identidades para resolver algunos ejercicios de práctica.
TRIGONOMETRÍA
Relevante para…
Aprender sobre las identidades de cociente con ejercicios.
TRIGONOMETRÍA
Relevante para…
Aprender sobre las identidades de cociente con ejercicios.
¿Cuáles son las identidades de cociente?
Las identidades de cociente son las identidades trigonométricas escritas en términos de las funciones trigonométricas fundamentales, seno y coseno.
Consideremos a las funciones seno, coseno y tangente. Si es que definimos a estas funciones en un triángulo rectángulo, tenemos lo siguiente:
$latex \sin(\theta)=\frac{O}{H}$
$latex \cos(\theta)=\frac{A}{H}$
$latex \tan(\theta)=\frac{O}{A}$
en donde, O es el lado opuesto al ángulo, A es el lado adyacente al ángulo y H es la hipotenusa del triángulo.
Dadas estas definiciones, podemos demostrar que $latex \tan(\theta)=\frac{\sin(\theta)}{\cos(\theta)}$, siempre y cuando $latex \cos(\theta)\neq 0$:
$latex \frac{\sin(\theta)}{\cos(\theta)}=\frac{\frac{O}{H}}{\frac{A}{H}}$
$latex =\frac{O}{A}=\tan(\theta)$
Hemos comprobado que podemos escribir a la función tangente como el seno del ángulo dividido por el coseno. Además, dado que la cotangente es la identidad recíproca de la tangente.
Podemos escribir a la cotangente como el coseno del ángulo dividido por el seno. Entonces, tenemos las dos identidades del cociente:
| $latex \tan(\theta)=\frac{\sin(\theta)}{\cos(\theta)}$ $latex \cot(\theta)=\frac{\cos(\theta)}{\sin(\theta)}$ |
Ejercicios de identidades de cociente resueltos
Las identidades de cociente trigonométricas son usadas para resolver los siguientes ejercicios. Cada ejercicio tiene su respectiva solución, pero intenta resolver los ejercicios tú mismo antes de mirar la respuesta.
EJERCICIO 1
Si es que tenemos los valores $latex \cos(\theta)=\frac{3}{11}$ y $latex \sin(\theta)=\frac{5}{11}$, ¿cuál es el valor de $latex \tan(\theta)$?
Solución
Usamos la identidad del cociente de la tangente para resolver este problema. Entonces, tenemos que dividir el valor del seno por el valor del coseno:
$latex \tan(\theta)=\frac{\sin(\theta)}{\cos(\theta)}$
$latex \tan(\theta)=\frac{\frac{5}{11}}{\frac{3}{11}}$
$latex \tan(\theta)=\frac{5}{3}$
EJERCICIO 2
Muestra que la identidad $latex \cot(\theta)=\frac{\cos(\theta)}{\sin(\theta)}$ es verdadera.
Solución
Para demostrar que la identidad dada es verdadera, podemos usar las definiciones de seno, coseno y tangente en términos de un triángulo rectángulo.
Entonces, sabemos que el coseno es definido como el lado adyacente (A) sobre la hipotenusa (H) y el seno es definido como el lado opuesto (O) sobre la hipotenusa, por lo que tenemos:
$latex \cot(\theta)=\frac{\cos(\theta)}{\sin(\theta)}$
$latex \cot(\theta)=\frac{\frac{A}{H}}{\frac{O}{H}}$
$latex \cot(\theta)=\frac{A}{O}$
Tenemos que la cotangente es igual al lado adyacente dividido por el lado opuesto, lo cual es correcto, ya que la cotangente es la función recíproca de la tangente.
EJERCICIO 3
Tenemos los valores $latex \cos(\theta)=\frac{5}{7}$ y $latex \sin(\theta)=\frac{2}{7}$. Determina el valor de $latex \cot(\theta)$.
Solución
En este caso, tenemos a la función cotangente, por lo que sabemos que podemos calcular su valor al dividir el valor del coseno por el valor del seno. Entonces, tenemos:
$latex \cot(\theta)=\frac{\cos(\theta)}{\sin(\theta)}$
$latex \cot(\theta)=\frac{\frac{5}{7}}{\frac{2}{7}}$
$latex \cot(\theta)=\frac{5}{2}$
EJERCICIO 4
¿Cuál es el valor de $latex \sin(\theta)$ si es que tenemos los valores $latex \tan(\theta)=\frac{12}{5}$ y $latex \cos(\theta)=\frac{5}{9}$?
Solución
Nuevamente tenemos a la función tangente, sin embargo, en este caso tenemos que encontrar el valor del seno. Usamos la identidad del cociente de la tangente y resolvemos para el seno:
$latex \tan(\theta)=\frac{\sin(\theta)}{\cos(\theta)}$
$latex \frac{12}{5}=\frac{\sin(\theta)}{\frac{5}{9}}$
$latex \sin(\theta)=(\frac{12}{5})(\frac{5}{9})$
$latex \sin(\theta)=\frac{12}{9}=\frac{4}{3}$
Ejercicios de identidades de cociente para resolver
Resuelve los siguientes ejercicios aplicando lo aprendido sobre las identidades de cociente. Selecciona una respuesta y verifícala para comprobar que obtuviste la solución correcta.
Véase también
¿Interesado en aprender más sobre identidades trigonométricas? Mira estas páginas: