Las identidades de suma y resta de ángulos son identidades trigonométricas usadas para calcular los valores de ángulos. Estas identidades pueden ser usadas para reescribir a los ángulos como una suma o una resta de ángulos comunes. Por ejemplo, para calcular el seno o el coseno de 15°, podemos reescribir al 15 como la resta de 45 y 30 ya que los valores de los senos y cosenos de 45° y 30° son los más comunes y son generalmente conocidos.
A continuación, aprenderemos a derivar las identidades de suma y resta de ángulos y las aplicaremos para resolver algunos ejercicios de práctica.
TRIGONOMETRÍA
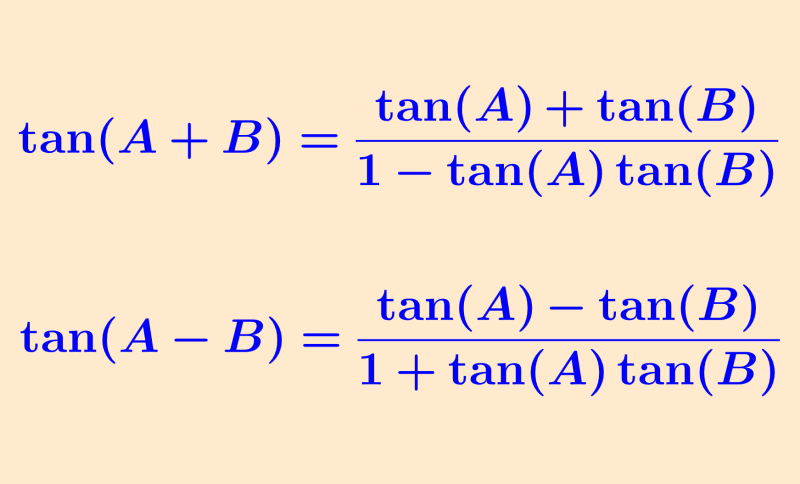
Relevante para…
Derivar y aplicar las identidades de suma y resta de ángulos.
TRIGONOMETRÍA
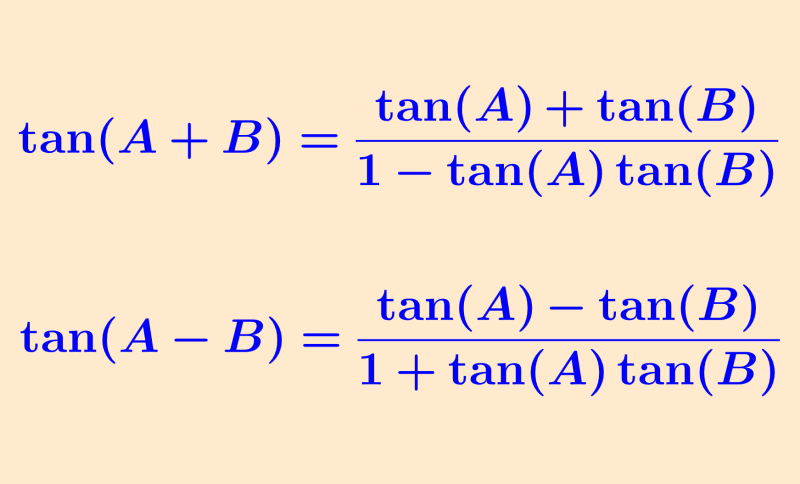
Relevante para…
Derivar y aplicar las identidades de suma y resta de ángulos.
¿Cuáles son las identidades de suma y resta de ángulos?
Las identidades de suma y resta de ángulos son identidades trigonométricas, las cuales pueden ser usadas para encontrar los valores de funciones trigonométricas de cualquier ángulo.
Sin embargo, el uso más práctico de estas identidades es para encontrar los valores exactos de un ángulo que puede ser escrito como una suma o diferencia de valores familiares para seno, coseno y tangente de los ángulos 30°, 45°, 60°, 90° y sus múltiplos.
Las identidades de la suma de ángulos son:
| $latex \sin(A+B)=\sin(A)\cos(B)+\cos(A)\sin(B)$ $latex \cos(A+B)=\cos(A)\cos(B)-\sin(A)\sin(B)$ $latex \tan(A+B)=\frac{\tan(A)+\tan(B)}{1-\tan(A)\tan(B)}$ |
Las identidades de la resta de ángulos son:
| $latex \sin(A-B)=\sin(A)\cos(B)-\cos(A)\sin(B)$ $latex \cos(A-B)=\cos(A)\cos(B)+\sin(A)\sin(B)$ $latex \tan(A-B)=\frac{\tan(A)-\tan(B)}{1+\tan(A)\tan(B)}$ |
Ejercicios de identidades de suma y resta de ángulos resueltos
Los siguientes ejercicios son resueltos aplicando las identidades de suma y resta de ángulos de seno, coseno y tangente. Intenta resolver los ejercicios tú mismo antes de mirar la respuesta.
EJERCICIO 1
Encuentra el valor exacto del coseno de 75° usando una identidad de suma de ángulos.
Solución
Podemos usar la identidad de la suma de ángulos de cosenos, ya que 75° es igual a la suma de 30° y 45°. Entonces, tenemos:
$$\cos(A+B)=\cos(A)\cos(B)-\sin(A)\sin(B)$$
$$\cos(30+45)=\cos(30)\cos(45)-\sin(30)\sin(45)$$
$latex =\frac{\sqrt{3}}{2} \cdot \frac{\sqrt{2}}{2}-\frac{1}{2}\cdot \frac{\sqrt{2}}{2}$
$latex =\frac{\sqrt{6}}{4}-\frac{\sqrt{2}}{4}$
$latex =\frac{\sqrt{6}-\sqrt{2}}{4}$
El valor del coseno de 75° es $latex \frac{\sqrt{6}-\sqrt{2}}{4}$.
EJERCICIO 2
Usa una identidad de resta de ángulos para encontrar el valor exacto del seno de 15°.
Solución
Podemos usar la identidad de la resta de ángulos de senos, ya que 15° es igual a la resta de 45° y 30°. Entonces, tenemos:
$$\sin(A-B)=\sin(A)\cos(B)-\cos(A)\sin(B)$$
$$\sin(45-30)=\sin(45)\cos(30)-\cos(45)\sin(30)$$
$latex =\frac{\sqrt{2}}{2} \cdot \frac{\sqrt{3}}{2}-\frac{\sqrt{2}}{2}\cdot \frac{1}{2}$
$latex =\frac{\sqrt{6}}{4}-\frac{\sqrt{2}}{4}$
$latex =\frac{\sqrt{6}-\sqrt{2}}{4}$
Esto significa que el valor exacto del seno de 15° es $latex \frac{\sqrt{6}-\sqrt{2}}{4}$.
EJERCICIO 3
Encuentra el valor exacto de $latex \cos(\frac{7\pi}{12})$ usando una identidad de suma de ángulos.
Solución
Usamos la identidad de suma de cosenos, ya que podemos expresar al ángulo como una suma de ángulos fáciles:
$latex \cos(\frac{7\pi}{12})=\cos(\frac{4\pi}{12}+\frac{3\pi}{12})$
$latex =\cos(\frac{\pi}{3}+\frac{\pi}{4})$
Usando estos ángulos en la fórmula, tenemos:
$$\cos(A+B)=\cos(A)\cos(B)-\sin(A)\sin(B)$$
$$\cos(\frac{\pi}{3}+\frac{\pi}{4})=\cos(\frac{\pi}{3})\cos(\frac{\pi}{4})-\sin(\frac{\pi}{3})\sin(\frac{\pi}{4})$$
$latex =\frac{1}{2} \cdot \frac{\sqrt{2}}{2}-\frac{\sqrt{3}}{2}\cdot \frac{\sqrt{2}}{2}$
$latex =\frac{\sqrt{2}}{4}-\frac{\sqrt{6}}{4}$
$latex =\frac{\sqrt{2}-\sqrt{6}}{4}$
Esto significa que el valor exacto del coseno de $latex \frac{7\pi}{12}$ es $latex \frac{\sqrt{2}-\sqrt{6}}{4}$.
Ejercicios de identidades de suma y resta de ángulos para resolver
Aplica las fórmulas de las identidades de suma y resta de ángulos de seno y coseno para resolver los siguientes ejercicios de práctica. Selecciona una respuesta y verifícala para comprobar que obtuviste la respuesta correcta.
Véase también
¿Interesado en aprender más sobre identidades trigonométricas? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
